Hay ciertos hechos con los que todos estamos familiarizados: que en el vacío uná pluma y una bala caen con la misma velocidad, a pesar de que en la atmósfera aquella tarda en llegar al suelo mucho más tiempo que ésta; que el serrín flota y la arena va al fondo cuando se colocan en un cubo de agua; que los lechos de los arroyos y de los ríos están constituidos por arenas cada vez más finas a medida que se acercan a su desembocadura; que un trozo de plomo llega al, fondo de un caldero lleno de agua antes que un guijarro del mismo tamano aproximado. Son todas éstas manifestaciones incontroladas de la fuerza gravitatoria y de la resistencia de fluidos que se emplean mucho en la separación de los minerales y en la de fases fluida y sólida en las ins-talaciones de preparación de menas.
La fórmula general de las leyes que regulan los movimientos relativos de las particulas y fluidos y de las partículas de distintos tamaños y pesos es bien conocida, y se han determinado los coeficientes en ciertas condiciones. La comprensión de estas leyes es esencial en casi todas, las separaciones empleadas en la preparación de minerales. Para llegar a esta comprensión juzgamos indispensable tener una idea de cómo se deduce, y creemos que ello justifica que dediquemos todo este capítulo al estaudio de aquellas condiciones, aunque las formas ideales consideradas nunca se encuentran en las operaciones comerciales.
En sentido restringido, la palabra sedimentación, es la deposición por gravedad de partículas sólidas en un medio flúído. Sin embargo desde el punto de vista tecnológico, la fuerza impulsora puede ser cualquiera que actúe a distancia; es decir, la gravitatoria, la centrífuga, la eléctrica o la magnética; la deposición puede ser en cualquier dirección, como, por ejemplo, la ascensión de burbujas de gas en una masa estacionaría de agua o el movimiento predominantemente horizontal de las partículas en suspensión en un ciclón de eje vertical; las partículas pueden ser sólidas, líquidas o gaseosas siempre que formen una fase distinta en el líquido sospensor. y, por último, al medio de suspensión no es preciso que sea un verdadero fluido, sino que puede ser, y con frecuencia es, una suspensión.
Para los fines del análisis, el caso más sencillo es el de una partícula única que se mueve bajo la acción de la gravedad en el seno de un flúído estacionario de extensión infinita. Este movimiento se llama sedimentación’ lare’:- Experimentalmente se ha demostrado que para todos los Fines prámicos la condición de un «fluido de extensión infinita» se satisface esencialmente cuando ni las paredes del recipiente; que contime el flúido ni otras partículas en suspensión distan menos de 10 a 20 dámetros de la partícula considerada.
Los resultados de un experimento muy completo realizado con partículas de minerales que se sedimentan en agua bajo la acción de la gravedad, se ponen de manifiesto en la figura 1. Limitan do, por ahora,
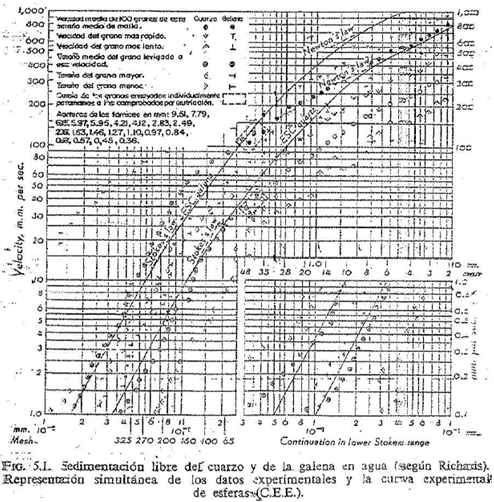
nuestra taención a los puntos que representan promedias de tamanos de granos y promedios de velocidades, podemos ver que para cada uno de los minerales, una curva continua construida con estros promedos rendrá tres secciones bien definidas: una superior, recta, con pendiente dél orden de 0,5, otra inferior, también recta, con pendiente del orden de 2, y una intermedia, curva. Los análisis; teóricos que; se presenan más abajo confirman que las partículas más gruesas se sedimentan con velocidades que varían en función de la rafz cuadrada del «diámetro» de la partícula, y que para las partfculas finas lás velocidades son proporcionales al cuadrado del diámetro de la partícula; Para partículas, que se encuentran en el intervalo de tamaños intermedio, el análisis teórico no ha podido aplicarse con éxito Sin embargo, la figura 1: nos dice que la velocidad de sedimentación es una función variable del diametro.
En estricto orden cronológico, la primera en desarrollarse: fue la relación de línea recta para las partículas mayores. Tal como lo desarrollo. Newton, este método consistía en deducir por separado la expresión general, de la fuerza gravitatoria que actúa sobre la partícula y la correspondiente resistencia de flúido y a continuación, igualar, estas expresiones para establecer las condiciones de equilibrio.
Para, simplificar, y teniendo en cuenta la facilidad de verificación experimental se considera una partícula esférica que cae. Para una partícula,de este tipo, y de acuerdo con el principio de Arquimedes la fuerza, gravitatoria que actúa es:
Fg = mg – m’g,…………………………………..(1)
en la que m y m’ son, respectivamente, las masas de la partícula y del fluido que desplaza. Para masas esféricas, la ecuación (I) se convierte en la siguiente:
![]()
El cálculo de la resistencia de fiúido de Newton se basa en los cuatro supuestos siguientes: 1) que las partículas del fluido en las que se introduce el cuerpo se encuentran ea reposo, pero con libertad para moverse; 2) que las colisiones entre dichas partículas, por una parte, y entre éstas y el cuerpo que se mueve a través de ellas, por otra, son elástícas 3) que la sección transversal del volumen de fiúido desplazado por un cuerpo que se mueve a través de él es igual a la proyección de dicho cuerpo en un plano perpendicular a su línea de movimiento, y 4) que la resistencia ofrecida al cuerpo es la misma que se ofrecería a una placa plana que tuviese la forma y orientación de esta proyección supuesta. Sobre la base de estos supuestos, en el tiempo t, una placa de este tipo desplazará una masa m» de fiúido y, al hacerlo, comunica a cada elemento de dicho flúido una velocidad proporcional a la suya propia, v. Por tanto:
m» = kpAvt,…………………………………………………………………(3)
en la que A es el área proyectada del cuerpo en la dirección del movimiento y k una constante de proporcionalidad. La resistencia, Rn es, igual a la cantidad de movimiento transmitido por segundo al agua, o
![]()
Puede, resultar aleccionador presentar la ecuación (4) en una forma que podríamos llamar energética:
![]()
En la que, comparándola con la ecuación (4), D = 2k. En la ecuación (5), pv2/2 tiene las dimensiones de una energía cinética por volumen unidad de líquido. La cantidad D es adimensional, y su valor es independiente de las unidades empleadas. Se la conoce con el nombre de resistencia específica o de coeficiente de retardo.
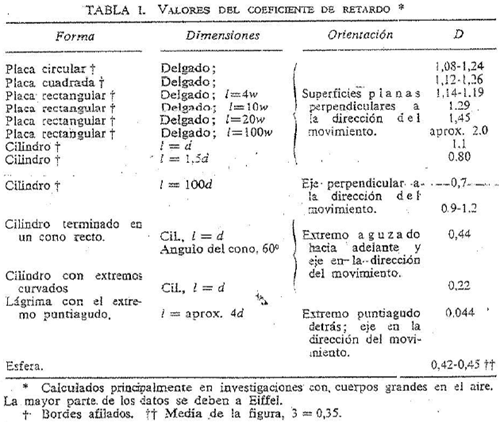
Experimentalmente se ha demostrado que D no es constante,, sino que varía con la forma del cuerpo y, en el caso de formas no simétricas, con su orientación respecto a la dirección del movimiento relativo de éste y del fluido. En la tabla 1 se dan los valores de D para varias orientaciones y formas geométricas.
Experimentalmente se demuestra que cuando el medio es el agua, se Iogra una velocidad prácticamente constante, lo que indica que se igualan Fg y RN en una pequeña fracción de segundo. Según esto, igualando las ecuaciones (2) y (5) y despejando v, tenemos:
![]()
en la que los subíndices limitan la aplicación a partículas esféricas y a velocidades en las que la resistencia de fluido se debe exclusivamente a la inercia. Este es el intervalo que corresponde a la línea recta superior de las curvas de la figura 1.
La forma corriente en la que se emplea esta relación entre v y d dentro de este intervalo de Newton en los problemas de preparación de menas, es:

donde a es un factor que relaciona el volumen de la partícula al diámetro y que para las esferas tiene el valor de 4/3. El valor de A para la galena, deducido de la figura 1, tiene un valor medio de 32, y para el cuarzo de 27.
Para cualquier sólido y fluido dado, la ecuación (7) tiene la forma, general y = kx½. Empleando logaritmos, tenemos:
Log y = ½log x + log k
que en papel logarítmico se traduce en una línea recta de 0,5 ,de pendiente, Las curvas de la figura 1 que nos dan los resultados de muchos, experimentos realizados con esferas tienen esta pendiente en sus extremos superiores y, hasta ese punto, proporcionan una justificación pragmática del desarrollo de Newton.
Empleando un método de análisis matemático, Stokes ha deducido una ecuación para la resistencia ofrecida por un flúído al movimiento de una esfera partiendo del supuesto de que cuando la, velocidad relativa es muy pequeña los efectos de inercia son despreciables, y la resistencia puede atribuirse exclusivamente á frotamiento interno (viscosidad) del flúido. Esta ecuación es la sígnente:
![]()
Tanto las fórmulas de Stokes como de Newton para la resistencia de flúidos pueden deducirse por el método de análisis dimensional. La experiencia diaria nos lleva a incluir las siguientes como probables variabas pertinentes:
1. La resistencia aumenta con la superficie transversal a la dirección del desplazamiento del cuerpo en movimento. Compárese, por ejemplo, la resistencia que
el aguá ofrece al movimiento rápido de la mano abierta según se vuelva la palma o el canto.
2. La resistencia aumenta, con La velocidad, relativa. Compárense los movimíentos rápidos y lentos de la nano abierta dentro del agua con la palma en la
dirección del movimiento.
3. La resistencia aumenta con la densidad del flüido. Compárese la resistencia que ofrecen el aire y el agua a movimientos análogos de la mano.
4. La resistencia aumenta con la viscosidad del flüido. Compárense los esfuerzos que háy que realizar para agitar ma masa de agua y otra de alquitrán de carbón o de melázas.
5. La resistencia varía con la corma del cuerpo. Compárense el movimiento de la mano con los dedos encogidos cuando se mueve a la misma, veiocidad con la palma o los nudillos dando frente al movimiento.
6. La resistencia varía con la forma rieantación del cuerpo. En este caso son aplicables los experimentos 1 y 5.
Una búsqueda persistente no la permitido poner de manifiesto más variables que lás que acabamos de citar y, por consiguiente, la relación completa se expresa en lo que sabemos diciendo que la resistencia del fluido al movimiento de un cuerpo es una función de la densidad y de la viscosidad de aquél, de la configuración y orientación del cuerpo, de su área proyectada en la dirección del movimiento y de la velocidad relativa o, en otras ptiabras:
![]()
y n = 7. [Véase el texto que sigue a la ecuación (2a) del capítulo 4.
Las dimensiones de las variables Q de la ecuación (10) son las siguientes:
R Fuerza, MLT-2.
A Area, que generalmente se expresa en función del «diámetro», d, que tiene las dimensiones L.
v Velocidad; LT-1.
p Densidad, ML-3
n Viscosidad, ML-1 T-1
v Forma, que es susceptible te especificarse en función de una cantidad lineal (dimensión L) para ciertos cierpos regulares, aunque no existe ninguna forma general de especificación a lá que pueda atribuirse una expresión dimensional general. Por tanto, para las fines del presente análisis debe tratarse como
si fuese un número puro.; es decir, que la solución debe circunscribirse a una forma determinada
o La orientación tampoco es sisceptible de una especificación dimensional, sobre la base de nuestros conocimientos actuales y, por tanto, debe tomarse como constante. Sin embarco, circunscribiéndose a la forma esférica se obtiene una orientación consunte
Limitada al caso de una esfera la ecuación (10) puede escribirse como a continuación se Indica;
![]()
en la que E es una constante que íesigna la forma esférica y la consiguiente orientación invariable. En este caso, el valor de n es 5, y, de las dimensiones dadas más arriba, m es 3,
En lo que se refiere a la seleccón de las variables Q la limitación se satisface escogiendo tres de ellas que caracericen respectivamente, a la longitud, al movimiento y a una propiedad del flüido: es decir; d, v y p. Así, nos quedan como términos característicos Px, R y r.
Hay n-m = 2 terminos J que se deducen de la ecuacion (10a)

Las ecuaciones dimensionales son:
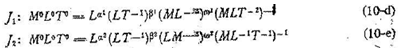
Las ecuaciones con los exponentes de la ecuacion (10-d) son:
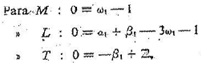
de las que, resolviendo el sistema de ecuaciones a1 = 2, B, = 2, j, = 1. .Análogamente, de la ecuación (10-e) tenemos que a2 = L, B2, = 1, w1 = 1 Sustituyendo estos valores de los exponentes en las ecuaciones (10-b) y (10-c), tenemos:

Entonces la ecuacion (10-a) toma la forma
![]()
Si D es un numero real que es una raiz cualquiena de la ecuacion (10-b):
![]()
La ecuación (11) nos dice, que la resistencia al movimiento relativo de una esfera sumergida en un fluido de-extensión infinita es el producto de los siguientes factores: una constante, 1E, que depende de la configuración y de la orientación, el cuadrado de una dimensión, d, del cuerpo que define su seccion transversal normal al movimiento, el cuadrado de la velocidad relativa, la densidad del flúido y una función de una cantidad, dv p/n. El valor de las constante y la determinación de la forma de la función f{dv-p/n) sólo puede obtenerse recurriendo a la experimentación cuantitativa. Sin embargo, es posible efectuar urna comprobación aproximada recurriendo a una comparación con los hechos cualitativos que se clan en la página 73 y 74. No cabe duda de que esta, ecuación concuerde con los hechos 1, 2, 3, 5 y 6. También pone de manifiesto que, para que cessacuerde con el hecho número 4, la forma de f{dv p/n) debe ser inversa, o, de otro ánodo, que en determinados tipos de movimientos relativos no se cumpla en verdad este hecho.
El procedimiento que se sigue para relacionar la ecuación (11) con el cúmulo de datos experimentales sobre el movimiento grarvitatorio de las esferas en los fluidos es el siguiente:
a. El término d2 se sustituye por A divídiendo la constante por n/4 y multiplicando el término d2 por la misma constante geométrica.
b Se déduce el factor 1/2 del término constante para unirlo a pv2 a fin de obtener pv2/2 como en la ecuacion (5),
c La aplicación de esta ecuación está limitada a la velocidad terminal vm (Véase página-72). Por tanto, la ecuación (11) se convierte en la siguiente:
![]()
que nos dice-que, para una esfera, la resistencia es proporcional al área transversal de la misma al cambio dé la energía cinética del flúido producido por el movimiento relativo y a una función de la viscosidad.
d. A continuación, la ecuacion (11-a) se transforma dividiéndola sucesivamente por el término constante y por R, m, y luego éste se sustituye por el peso de la esfera sumergida de la ecuación (2). Esto se basa en que, siendo la gravedad la única fuerza que origina el movimiento, cuando se alcanza una velocidad terminal constante (vm) la aceleración es cero, y la resistencia del flúido se iguala con la fuerza: gravitatoria: Entonces tenemos que:

Las ecuaciones (11-b) y (12) nos dicen que el producto de dos funciones es una constante. En esta fase la constante se desconoce, y depende de la forma de las funciones. Al llegar a este punto, fray que proceder a la realización de experimentos en los que, dando valores a las variables contenidas en las funciones y asignando formas, convenientes a las funciones, se llevan los resultados a una gráfica. Esto no podía hacerse en el caso de la, ecuación (10). capitulo 4, porque no se, disponía de datos experimentales pero existen muchos de la sedimentación líbre de esferas én el seno de flúídos. En la figura. (2) los vemos una vez llevados a una gráfica en la que D„ de la ecuación (13), corresponde a las ordenadas, y N, de la ecuación (14), a las abcisas.
e Los datos que se han llevado al gráfico abarcan una escala de densidad de partículas que va desde la del aire (1,29 10-3. g/cm3) a la del mercurio (13,35), e incluye gases, líquidos y, sólidos; las densidades de los medios van desde la del aceite de colza (0,917) a la anilina (1,04), y las viscosidades desde la del agua (0,014 poises) a la del aceite de ricino (6,53); los diámetros de las esferas van desde 0,07 centímetros para el aire hasta 0,8 cm para el aceité, y las velocidades oscilan entre 0,014 y 133 cm/seg; aún así una curva continua muestra la relación a lo largo de toda la gama.
La importancia de esta curva experimental reside en que demuestra que, en cualquier movimiento relativo de un sólido y de un flúido, existe una condición tal que a cada valor de la relación dv p/n corresponde otro de la cantidad kgd(a-p)/pv2, siendo k =4/3 cuando la superficie de contacto entre el flúido y el sólido es una esfera. Fue Osborne Reynolds quien descubrió que la cantidad dv p/n caracteriza, el flujo de flúidos, y, en su honor se llama número de Reynolds. La cantidad concomiante, que tiene las dimensiones aparantes de fuerza por masa unidad por aceleracon unidad, es el coeficiente de resistencia.
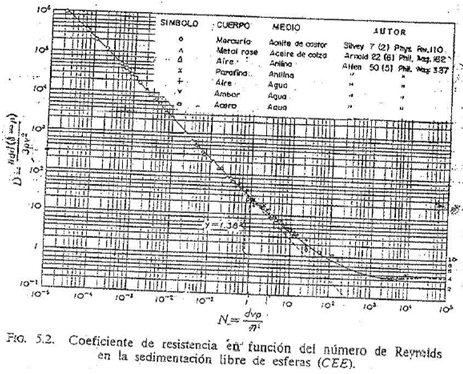
La expresión para aquella parte de la curva que se encuentra a la izquierda de N = 0,9 (aprox.), es la de una línea recta, y = px + b, en la que:

Tomando antilogaritmos, multiplicando aaiembro a membro la ecuación resultante con la (2) y despejando. F, tenemos:
![]()
Pero como v es la velocidad límite, se sigue verificando que F, — Rm de lo que se deduce que
![]()
Esto constituye una confirmación experimental del desarrollo teórico de Stokes, por cuya razón se emplea el subíndice S para indicar que se refiere al intervalo de Stokes
Igualando el valor de R de la ecuación (9) al de F de la (2) y despejando v tenemos:
![]()
g. La ecuación de Newton para la velocidad Línme [ecuación (6)] puede deducirse de modo análogo a partir de la figura 2, admitieodo que la parte de la curva que se encuentra a la derecha de N = 2.000 tiene la forma y = Const.
h. Hasta la fecha ha sido imposible obtener una expresión similar para aquella parte de la curva de la figura 2 comprendida entre N = 0,9 y N = 2.000, ni tampoco ha sido posible simplificar más la ecuación (11-a) para esta región por otros medios; Sin embargo, el experimento y la. experiencia reunida, unidos a la consderación de las formas de las ecuaciones (5) y (9), y le la forma de la figura 2, nos llevan a la conclusión que en esta expresión han de figurar p y n elevados a potencias que varían con N (o, lo que es igual, en función de las condiciones del flujo) entre los límites 1,0 y 0 para n y 0 y 1,0 para p. En otras palabras, a los movimientos relativos de las partículas en los fluidos sometidos a 1a fuerza gravitatoria, sólo se opone el rozamiento interno del fluido elevado a la primera potencia cuando las velocidades son bajas, y la inertia de dicho fluido elevada a la primera potencia cuando aquéllas son altas, pero en la zona intermedia intervienen tanto el rozamiento interno como la inercia, que varían de modo inverso.
Desde el punto de vista práctico, el problema esriba ahora en obtener un ábaco que pueda emplearse de manera fácil en esta zrna intermedia.
El examen de la figura 2 nos dice que puede realizarse la entrada con una or denada deducida de los valores conocidos de d v, 8 y J. y que el valor de n puede calcularse del correspondiente de N. De hecho este es el método empleado en los viscosímetros de caída de bola. Pero si se desea a pasar de v o d hallar el valor del otro el método és indiréctó y fatigoso, porque ambas cantidades forman parte de la ordenada y de la abcisa. Por tanto, el problema específico es encontrar funciones en las que se elimine una u otra de estas cantidades, que debe ser la, que constituye el término desconocido a calcular por medio del ábaco.
El examen de las ecuaciones (13) y (14) pone de manifiesto que d se elimina en la función:

o en su inversa. Esto nos permite partir de valores conocidos de v para determinar los correspondientes de d. En la mayor parte de los problemas de preparación de minerales, el valor que se busca es, sin embargo, la velocidad de caída de una partícula de tamaño conocido. Por esta razón v debe eliminarse en la función de entrada, como es la siguiente:
![]()
La figura 3 es un gráfico de B en función de N.

El desarrollo que acabamos de describir a partir de párrafo que termina con la ecuación (9) constituye un ejemplo escálente de la utilidad y capacidad del método de análisis dimensional Es útil resumir cómo sigue las etapas que de un modo general se siguen en el desarrollo del análisis de un determinado fenómeno.
1. Delimítese y defínase el fenómeno con precisión. En el capítulo 4 era la fuerza ejercida por un campo magnético sabre una partícula magnética que se encontraba en éste, y no el problema más complejo de la separación magnética. En este capítulo se ha tratado de la resistencia ofrecida por un fluido en reposo al movimiento relativo de un cuerpo que se encuentra en él, y mo, por ejemplo, el problema de las velocidades relativas de una masa de partículas de distintos tamaños, densidades y formas en un flúido en movimiento. Pues aunque sábemos que es éste el problema que en la práctica se presenta, resulta, también tan complejo que, tomado en su conjunto, no hay modo de atacarlo.)
2. Hágase una relación de todas las variables que la experiencia de tipo cuantitativo, cualitativo o semicuantitativo demuestra que influyen en la magnitud del fenómeno delimitado y definido. (Véanse los párrafos numerados de la página 80.)
3. Sígase la marcha matemática descrita en las ecuaciones (1) a (9) del capítulo (4) y (10-h) del capítulo 5.
4. Efectúense experimentos cuantitativos en los que intervengan los variables que aparecen en los productos adimensionales en la funcón de la última ecuación y llévense los resultados a un gráfico empleando los productos adimensionales como ordenadas. Obsérvese que si sólo tenemos dos de estos productps, el gráfico será una curva, si ues una superficie, etc.
5. Empléense curvas como se hace en el desarrollo de la ecuación (15). Sí resultara una superficie, y se modela, deben limitarse las emaciones, a ser posible, por planos paralelos al de dos ce los ejes del modelo.
6. Si las ecuaciones de las curvas o de las superficies no pueden resolverse, los datos llevados al gráfico aun pueden ser útiles recurriendo al método de las ecuaciones (17) y (18).
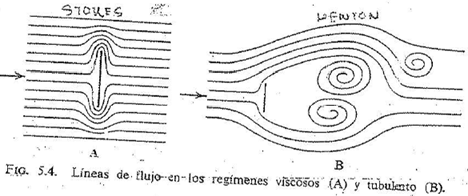
Se logra comprender mejor la naturaleza de las resistencias de los fluidos estudiando las líneas de flujo de un flúido que discurre rodeando un cuerpo, sumergido en él. Se presentan dos casos en la figura 4. En la 4-A (régimen de Stokes) el movimiento relativo es muy lento, y el flujo se conoce con el nombre de viscoso, mientras que en la 4-B (régimen de Newton) el flujo es rápido, se caracteriza por los remolinos que se forman detrás del cuerpo y se conoce con el nombre de turbulento.
Experimentalmente se demuestra que en la zona de los remolinos la presión es más baja que en el frente de la placa. Por el teorema de Bernoulli la presión y la velocidad de una corriente horizontal de flujo uniforme están relacionadas por la ecuación:
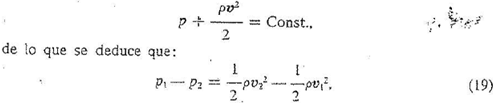
en la que los subíndices l y 2 corresponden a la parte anterior y posterior de la placa respectivamente. Ésta ecuación nos dice que al pasar alrededor de ia placa, la energía potencial de un flujo sin turbulencia se transforma en energía cinética del fluido en los remolinos.
Por definición R/A vanía proporcionalmente a p1 — p2. De esta relación y de la ecuación (19) tenemos que:
![]()
Experimentalmente se demuestra que en la ecuación (4), fc.es prácticamente constante al medir las resistencias de un cuerpo de configuración y orientación dadas en un intervalo grande de v, y también que v de la ecuación (20) varía en función de v1 Por tanto, de las ecuaciones (19) y (20) se deduce que la resistencia de un fluido en régimen turbulento se debe principalmente a la diferencia de presión entre la parte anterior y posterior del cuerpo sumergido, integrada a todo el cuerpo, y cuya resultante tiene la dirección de la línea de flujo.
En el caso de un flujo no turbulento (figura 4, A) éntre las dos caras del cuerpo sumergido, no existe una resistencia de presión medible; Por tanto, la totalidad de la resistencia es la que ofrece el fluido al deslizamiento de unos filetes con respecto a otros, sucesivamente desde el que está, inmovilizado en la superficie del cuerpo hasta el igualmente inmóvil que está en contacto con las paredes del recipiente. Es la viscosidad la única propiedad del fluido que se utiliza en la ecuacion (9).
La Importancia decisiva de la configuración y de la orientación, factores ambos, que, en efecto, se despreciaron en el desarrolo de la ecuación (10), salta a la vista cualitativamente cuando observamos las velocidades relativas de caída de un naipe cuando lo hace solo o formando parte de otros de la baraja desde una altera considerable. Desde el punto de vista cuantitativo, se demuestra lo mismo al comparar las, curvas de la figura 1 con los puntos dispersros. Estas curvas se trazaron a partir de la figura 2, mientras que los puntos dispersos, corresponden a resultados obtenidos de los experimentos con fragmentos minerales reales. Estos puntos no corresponden a experimentos controlados con tanto cuidado como las curvas obtenidas para, el caso de las esferas, debido a que para los fragménteos de minerales; es prácticamente imposible definir con exactitud el valor de ¿. Sin embargo, en tamaños que nominalmente son más gruesos que 1 mm, las partículas más rápidas, que probablemente en mudaos casos unían, volúmenes y, por tanto, pesos en inmersión tan grandes o mayores que los de las esferas del mismo diámetro nominal que dichas partículas. caían, con velocidades que, por término medio, eran tu 30 por ciento inferiores a las de las esferas. Esto sólo puede atribuirse a la forma y a la orientación.
Afortunadamente, desde el punto de vista del empleo de la curva obtenida para las esferas de preparación de minerales, el carácter aproximads de las operaciones industriales, y hasta de laboratorio, es tal que la relación, v-d de los granos de cualquier mineral se traduce en una franja ancha más bien que en una línea. En la figura 1 vamos que las curvas de las esferas tienden hacia el promedio de las velocidads de los granos de la parte inferior de la zona intermedia y en la de stokes y, por tanto, pueden emplearse para diseñar y analizar. En cunto a la zona superior, si el ingeniero quiere hacer ciertas concesions a un simulacro de precisión, los datos de la figura 1 constituyen un punto de partida tan bueno como otro cualquiera.
Deie comprenderse con claridad que las curvas obtenidas para las esferas son aplicables exclusivamente a esferas aisladas que caen bajo la influencia de la gravedad en el seno de un flúido en reposo y en, un recipiente de dimensiones horizontales muy grandes con respecto al diámetro de la esfera. En sus experimentos, Ladenberg determinó que los efectos de retardo no son apreciables hasta que la relación dil es superior a 0,045, siendo l la distancia de la partícula a la pared del recipiene o a otra partícula cualquiera. Si el movimiento del fúído es ascendente, constante y uniforme, el movimiento relativo de h esfera y del flúido permanece invariable prescindiendo del valor de dil pero el movimiento neto de la partícula con respecto a un punte fijo que es lo que se mide, es la suma vectorial del movimiento relativo partícula-fluido y del de este último. Sí el flúido tiene movimiento turbulento (N > 2.000 aproximadamente), esta regla no es rigurosamente exacta, aunque sí bastante aproximada. La relación critica dil define los límites de la caída libre para las curvas obtenidas con esferas.
En la terminología de preparación de minerales, el término caída libre expresa algo may distinto de la definición que se acaba de dar. En primer lugar, implica que, aunque existen muchas partículas próximas en una sección horizontal dada de una cámara de sedimentación en un instante cualquiera y que estén tan cerca unas de otras que en cierto modo se influyan mutuamente en su caída, y aunque choquen entre sí de modo infrecuente, se puede continuar considerándolas en régimen de caída libre en el sentido , más estricto de la palabra, aunque se guarden cieñas reservas en lo que se refiere a la predicción de su movimiento de acuerdo con la discusión anterior de la figura l. En otras palabras, sí, como nos dice esta figura, se considera que la velocidad de sedimentación de un género clasificado en una criba (por muy estrechos que sean los límites de ésta) que comprende un intervalo de tamaños y no un valor determinado, tendrá un margen de variación suficiente para que queden englobados los efectos mutuos de las partículas dentro de la sedimentación de caída libre a escala industrial (véase Flocuiación, capítulo 8). Este mismo pone de manifiesto que existe una relación más bien de franja que de línea, lo que nos permite prescindir de tener en cuenta los intentos de Wadell para definir un factor de forma al resolver los problemas de diseño industrial.
La razón de isodromía es una cantidad que tiene por objeto comparar las características de sedimentación de dos cuerpo so dos clases de cuerpos distintos en condiciones análogas, o bien los efectos que al variar el régimen, del flujo producen en el comportamiento de la sedimentación de las partículas. La razón de ispdromía se define como la de los diámetros de las partículas de distintas densidades, peró de iguales velocidades límites de sedimentación en idénticas condiciones ambiente. El diámetro mayor se toma como numerador de la fracción que expresa la relación, por cuyo motivo la razón de isodromía es un número siempre mayor que a. La relación puede deducirse de modo racional para partículas de la misma forma igualando, las expresiones de las velocidades límites de sedimentación de partículas de distintas densidades y despejando de la ecuación resultante la relación buscada. Así, pues, para esferas dentro del intervalo de Newton, al igualar los valores de v de la ecuación (6) de partículas ligeras y pesadas, respectivamente, y elevando al cuadrado para quitar radicales, tenemos:
![]()
De la que:
![]()
Análogamente, para el intervalo de Stokes de la ecuación (16), tenemos:
![]()
Como la relación v-d en el intervalo intermedio no se puede expresar de modo racional, no se puede formular para este intervalo una expresión de la razón de isodromía.
Aplicando las ecuaciones (21) y (22) a esferas de cuarzo y de galena en agua, obtenemos los valores ZN e> s = 3,93 y Zse. s = 1,97. Para las esferas véase figura 1.
PREGUNTAS DE REPASO
1. Definir: caída libre; flúido de extensión infinita tal como se aplica en la caída libre; coeficiente de resistencia; ecuación «completa»; intervalo de Newton; intervalo de Stokes; número de Reynolds: régimen de flujo laminar; régimen de flujo turbulento; flúido viscoso; razón de isodromía; sedimentación.
2. Cuáles son los cuatro supuestos sobre los que se basa el desarrollo analítico de la ecuación de Newton de la caída libre?
3. Cuáles son las limitaciones para la aplicación de la ecuación de Newton para determinar la velocidad de caída libre tal como se ha desarrollado aquí?
4. Desígnense las variables que intervienen en una ecuación «completa» de la resistencia de flúido.
5. Cuál es la naturaleza de la resistencia de flúido en el intervalo de Newton?
6. Qué se supone que es la naturaleza de la resistencia del flúido en el caso de partículas muy pequeñas?
7. Enumérense las generalizaciones sobre las que se basa el método de análisis dimensional.
8. Valiendose de ejemplos conocidos distintos a los que se dan en el texto, hágase una relación de los factores que desempeñan un papel en la resistencia que ofrece sin cuerpo estacionario al flúido que se desliza a lo largo de él.
9. Dar la función general que relaciona la resistencia del flúido al movimiento de las partículas en éste, a las propiedades de dicho flúido y del cuerpo.
10. Qué es el número de Reynolds?
11. Qué condiciones esenciales se impusieron en los experimentos sobre los que se basa la figura 2?
12. Qué se deduce del hecho que el gran número de datos del párrafo e de la página 82 nos da una curva regular cuando se lleva a un gráfico?
13. Por qué no es posible definir con precisión el «diámetro» tratándose de fragmentos minerales? ‘
14. Por qué podemos asegurar que las desviaciones de las curvas obtenidas para esferas de los puntos de las partículas más rápidas de la figura 1 se deben indudablemente a los factores de forma y de orientación?
15. Esbócense los filetes del flujo lento de un flúido a lo largo de una esfera V las líneas que seguirían las partículas en el flujo turbulento.
16. Cuál es el efecto de los remolinos sobre la presión que existe en un flúido?
17. Dese una: relación de varios ejemplos muy corrienets de sedimentación.
18. Cuál es la característica común de las fuerzas impulsoras de separación en la sedimentación? Tiénen una dirección común’? Cuáles son las fuerzas resistentes?
19. Qué nos dice la figura 1 sobre el carácter de la relación que existe entre a) tamaño de partícula y velocidad de sedimentación; b) peso especifico de la
partícula y velocidad de caída.
20. Calcúlese la fuerza ejercida sobre una esfera de 1 cm de diámetro por el agua que se desliza a lo largo de ella a una velocidad de 600 mm/seg.
21. Calcúlense las velocidades relativas de una esfera de acero de 1. cm de diámetro (p e, 7,83) que cae libremente en el aire y en el agua.
22. Calcúlense las velocidades relativas de un cilindro recto y de una esfera de los mismos peso y diámetro, que caen libremente en el agua, partiendo del supuesto de que el eje del cilindro permanece en la línea de dirección del movimiento.
23. Determínese el valor de A de la partícula de galena de dos mallas más rápida de la figura 1.
24. A qué tamaño aproximado de partícula corresponde la curva obtenida para una esfera de galena cuya pendiente es 1,0? Para el cuarzo?
25. Calcúlese el número de Reynolds para el movimiento relativo de 120 centímetros/segundo entré el aire a temperatura y presión normales y una esfera de 10 m de diámetro. En qué dimensiones se puede dar la respuesta? Dar la ecuacion de unidades.
26. Calcúlese la fuerza ejercida sobre una esfera de 5-u por una corriente de aire que se desliza a lo largo de ella a una velocidad de 100 mm/seg,
27. Si el aire se desplazase verticalmente hacia arriba en un campo gravitatorio, determinar si la esfera (suponiéndola de cuarzo) de la pregunta anterior caería o subiría.
28. Calcúlense las velocidades relativas de una esfera de acero de l-n de diámetro cuando cae libremente en el aire y en el agua,
29. Desarrollar la ecuación de Newton para la caída gravitatoria en un fluido como se indica en el párrafo g, página 84.
30. Calcúlese el coeficiente de retardo para un estera de cuarzo en las condiciones que rigen en la pregunta 25. En qué dimensiones se puede dar la respuesta?
31. Determínense las relaciones de caída Libre (Z,) para el cuarzo y para la galena en el aire en el intervalo de Newton; en el cloroformo (p = 1,50); para ambos flúidos en el intervalo de Stokes.
32. Determínese el valor de v para un valor dado de d a partir de la figura 2 y viceversa. Compruébense las respuestas empleando las figuras 1 y 3.
