The dependence of the power demand of a mill on the nature of the pulp does not appear to have received a great deal of study, and, in general, observations on this matter take the form of general statements. For example, Taggart states that, other things being equal, wet milling requires 60-90 % of the power for dry milling. This view is confirmed by calculations of the present authors, based on figures for two mills of about 8 ft diameter and 45 ft long kindly made available by Messrs. Edgar Allen & Co. In this case the power as calculated by the formulae of Rose and Evans was in extremely good agreement with the observed power requirements of the mill when dry grinding (within 5%). However, the power calculated on the basis of dry-grinding formulae with modified charge density was found to be about 20 % higher than the actual demand of the mill when grinding wet.
It would be expected that a fine “smooth” fluid pulp would reduce the power demand, since such a pulp would act as a lubricant to the mill charge and so reduce the equilibrium displacement of the centre of gravity of the charge. This reduction of the power requirement of the mill is probably bound up with the phenomenon of “slumping” of the charge, mentioned earlier. More viscous pulps would, by increasing the displacement of the charge, lead to increased power consumption. With increasing “tackiness” of the pulp, a reduction of the power requirements would be expected, since, in such a case the balls might adhere so well to the shell that a part of the charge is spread over the shell and, thus, is balanced about the axis of rotation. This decrease in power demand with pulps of increasing thickness is in accord with the observations of Gow, Guggenheim, Coghill and Campbell, but these workers did not carry the tests to the point where the balls adhered to the shell of the mill. This effect is, however, also observed in mills which are used for the dispersion of pigments in varnish, and similar duties, and so is very real.
From what has already been said about the interaction between the coefficient of friction and the magnitude of the ball charge, it would be expected that the effect of the change in pulp conditions would be relatively more important in mills for which the charge is small. This conclusion in fact follows from the observations of Gow, Guggenheim, Campbell and Coghill. Thus it would be expected that, for large fillings, the effects of the variation of the pulp characteristics would be, largely, in accordance with what would be expected to result from the consequential changes in the coefficient of friction involved.
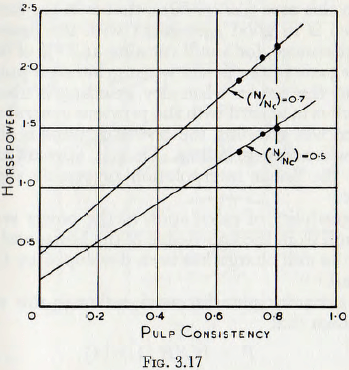
In view of the lack of data on this subject, it would appear that the best corrections for pulp characteristics which can be made is to assume that, for very thin pulps and moderate values of J and (D/d) the power required is 60% of that for dry milling, and then to use a linear interpolation for less liquid pulps. For larger mill fillings or greater values of (D/d) the reduction in power would be less than for the previous case and the multiplication factor should be modified accordingly. The general correctness of this view is supported by Fig. 3.17 in which the results of tests by Gow, Guggenheim, Campbell and Coghill, are plotted. Although these points are small in number and rather closely spaced they give lines which when extrapolated to zero pulp density give 0.22 and 0.45 horse-power as the powers to drive the mills without pulp charge; these figures being in the ratio 2.05 to 1.0.
Reference to equation (3.9), however, shows that, all other variables being maintained constant, the ratio of the powers is proportional to the ratio of the square of the speed; in this case (0.70/0.50)², that is in the ratio 1.96 to 1.0, which is in good agreement with the figure 2.05 to 1.0. Furthermore, for a mill running at 70 % of the critical speed the ratio of the power when grinding a pulp of 50 % density to the power when dry grinding is about 0.6 to 1.0: which is in accord with the previous general statement that when wet grinding the power demand is about 60 % of that when dry grinding. Thus it appears that, very roughly, the linear interpolation previously suggested is adequate.
The possibility of calculation of the power required to drive a mill from the knowledge of the horizontal displacement of the mill charge has been developed by Carey and Stairmand.
From the principles discussed earlier in this work, it is easily shown that
P = W N Hk (1/3.14) ……………….(3.22)
where P is the power input to the shell in kilowatts, to maintain the displacement of the charge, W is the weight in tons, of the grinding media plus powder, N is the mill speed in r.p.m. and Hh is the horizontal displacement in feet of the centre of gravity of the charge. Thus, the power input may be calculated provided the value of Hh can be obtained.
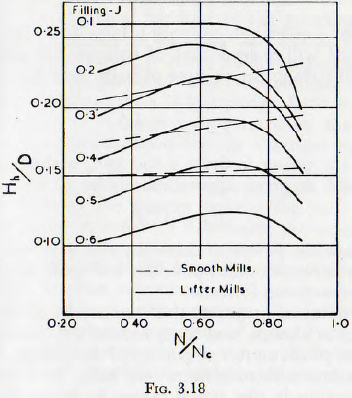
For this purpose Carey and Stairmand furnish a graph which gives the value of the ratio Hh/D (D is the mill diameter), in terms of the mill filling and the ratio of the speed of rotation of the mill to the critical speed; this graph being shown in Fig. 3.18. These curves are stated to be applicable to mills having diameters ranging from a few inches to several feet and, in practice, to give reasonably reliable results.
Analysis of this method in the light of the previous discussion shows that the effects of the weight of the charge, and so ∅(1 + 0.4σ/q), are included. Also the effects of
∅1′(N/Nc), ∅3(J) and of lifters are included, and so it appears that only variables which have been shown to be of comparatively minor importance are omitted. Thus, it would be expected that this treatment would have an accuracy sufficient for most practical purposes.
Effect of Pulp Density on Selective Grinding
In Fig. 6.4 are plotted curves, again according to Coghill and Devaney, which show the effect of pulp density upon selective grinding and it is at once evident that a more rapid reduction of the larger fractions is obtained with a pulp of moderate thickness than with a very thick one. The probable explanation of this phenomenon is that with a fluid pulp the fine material is washed from between the crushing surfaces, and so is not subject to further grinding. In addition, cleaning the grinding zone of such material leads to a higher efficiency of grinding of the large particles remaining.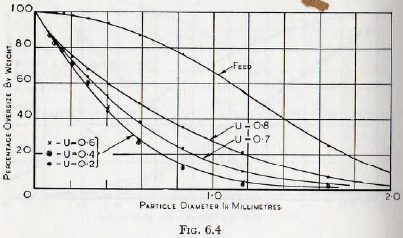
Thus, both from the point of view of rate of production of surface and of improved grinding of the larger materials, it is desirable that the pulp should be of moderate consistency.
Although there is not much evidence on the point, it appears that the size distribution curves of the products from mills with exit passages of large and small diameter are very similar. Thus selective grinding is but slightly controlled by variation of this dimension.
At this point it is of interest to consider, briefly, the conditions necessary for maximum efficiency in a mill; the efficiency being defined by the equation
η = E x Increase of surface/unit time/Energy input/unit time ……………………(6.1)
Consideration of the treatment of Chapter 3 will show that, for practical purposes, the power input to a mill is given by
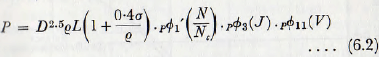
the effect of variations in the other dimensionless groups being small.
Similarly, consideration of Chapter 5 shows that the rate of production of specific surface, S/t, is given by
the variations of the other dimensionless groups being, under normal conditions, negligible.
Here the pre-suffix P or S attached to ∅, denotes that the power or the surface production, respectively, is a function of the dimensionless quantity which follows.
The total surface, S, produced is, however, proportional to the product of the specific surface produced and the volume of the mill. Thus the rate of production of total surface is given by
When equations (6.2) and (6.4) are substituted into (6.1) the quantities D, q, L and E cancel and the mill efficiency is given by
From this equation it follows that, for given values of (N/Nc), (J), and (V), the efficiency of the mill is independent of size.
In Fig. 6.5 the curves of power input to a dry mill, computed from the results of Chapter 3, and the rate of increase of specific surface, from Fig. 5.17, are plotted on
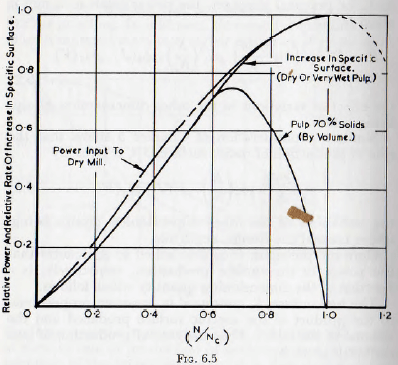
a base of (N/Nc). From this figure it is seen that, for the milling of a dry powder, or a very fluid pulp, there is fair agreement between the curve of power input and that of the rate of production of specific surface, for all speeds up to the critical. For the milling of moderately dry pulps there is also fair agreement for speeds up to about 70% of the critical. Thus, for these two cases the mill efficiency may be considered to be sensibly independent of the speed of the mill.
It is also probable that for speeds above 70% of the critical the power demand would fall away when moderately dry pulps are undergoing milling and so, in this case also, the mill efficiency would remain sensibly independent of the mill speed. Experimental evidence on this point is lacking, however, so a final conclusion cannot be safely drawn, for this case.
It appears to be safe to state, however, that, for all practical milling conditions, the mill efficiency is sensibly independent of the speed of the machine.