The factors upon which the rate of flow of the pulp through a mill depends appear not to have received extensive investigation. In an article by Anselm translated by Pearson a method for the calculation of the time of passage of cement through a ball mill was given. The basis of the method is that the volume rate of throughput is known and it is assumed that the surface of the powder is coincident with the surface of the ball charge. It follows that the average throughput velocity is the quantity of flow divided by the area open to flow. From this average velocity the time for a particle to traverse the mill may be computed. This treatment does not, however, indicate whether, for a given rate of flow, the surfaces of the powder mil the ball charge will coincide or not. For example, with discharge by peripheral ports, it would be expected that the surface of the powder charge would slope quite sharply from the entrance to the exit end. With a trunnion overflow mill, however, by the nature of the design, a steep slope is precluded and there would be but a small “head” to maintain flow.

The small amount of evidence relating to the rate of flow through a rod mill which is available can again best be studied by the use of dimensional analysis. It would appear to be reasonable to expect that the mass rate of throughput Q tons per hour would depend upon the diameters of the mill, of the ball and the particle, D, d and b respectively, upon the length of the mill, L, and the speed of rotation, N. It would also be expected that the throughput would depend upon the kinematic viscosity of the pulp v, the density of the pulp σ, upon the exit diameter of the mill u and upon the mill filling J.

When the method of dimensional analysis is applied to these variables it is found that

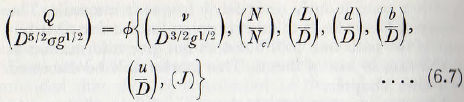
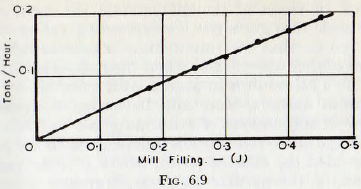
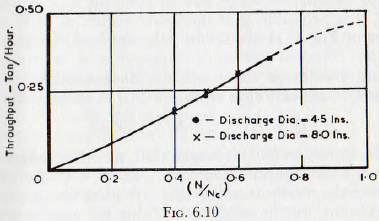
The kinematic viscosity of the pulp would doubtless depend upon the consistency of the pulp, the size of the particles in the pulp and on the cohesive properties of the solid materials when immersed in the liquid phase. Unfortunately there is not nearly sufficient published data to allow a complete study of this equation, but the data of Coghill and Devaney plotted in Fig. 6.9, indicate that the throughput varies directly as the mill filling, J, at least for values of filling up to 50%. Similarly, from Fig. 6.10, it would appear that the throughput varies directly with the speed of rotation, for speeds up to about 70% of the critical. At some point above this speed the curve would be expected to become horizontal, since at the critical speed the charge would be spread around the mill and horizontal flow would then be unlikely. Finally, it would be expected that the ratio of the average size of the passages between the grinding media to the particle size would be a controlling factor in the flow of the pulp; since if the particles are larger than the passage dimensions there is mechanical sieving, whilst, if the particles are relatively small, the flow would be limited only by the effective viscosity of the pulp.

Now, from the geometry of a bed of granular materials, the mean pore size is directly proportional to the particle size. Thus, the ratio (d/b) would be a controlling variable. This group is not inconsistent with equation (6.6) since (d/b) = (d/D) ÷ (b/D).

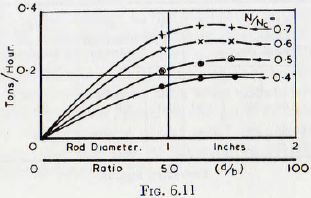
It is improbable, however, that, in practice, the ratio (d/b) would exceed about 40-50, since this would give rods of excessively large size in relation to the particle. Thus, it is probable that the lower values of (d/b) on the curves of Fig. 6.11 would be relevant and, for this case, Q ∝ d/b.In Fig. 6.11 are plotted the quantities of flow through a rod mill, in terms of the diameter of the rods. A subsidiary scale also gives the corresponding values of (d/b) and it is seen that the rate of flow is substantially independent of the ratio of (d/b) when the ratio is greater than about 50. This result is in accord with a finding by one of the present authors, Rose and Barnacle, working on the flow of suspensions of solid materials through pipes, that the hydraulic resistance is independent of the particle size provided the ratio of (D/d), where D is the pipe diameter and d, the particle diameter, is greater than about 30 to 40.

Thus, insofar as there are the data available for the analysis, it appears that equation (6.7) can be reduced to

From equation (6.7) it is seen that, all other things being equal, the throughput should vary as D2.5. Unfortunately data for the verification of this equation are practically non-existent, but those given in Table 6.2 suggest that the observed throughput is roughly in accord with this expression.