Table of Contents
Analytical Balance Principle
In this place it will be sufficient to describe the usual chemical balance, designed to carry in each pan a load up to 100 gms. This balance can be obtained at a reasonable figure, and sensitive to 1/10 of a milligram (0.0001 gm.). In the section on Assaying the student will find two other forms—Pulp Scales and the Assay Balance— mentioned. The pulp
Scales are cheap, and sensitive to about 1/100 gm., and serve well for weighing quantities of 20 gms. and over. The assay balance is more sensitive than the chemical balance, but its range is shorter (from .5 gm. to .00005 gm.). The student who understands the chemical balance, its adjustments and methods of checking and weighing, will have little difficulty in using the finer assay balance.
Analytical Balance Parts and Function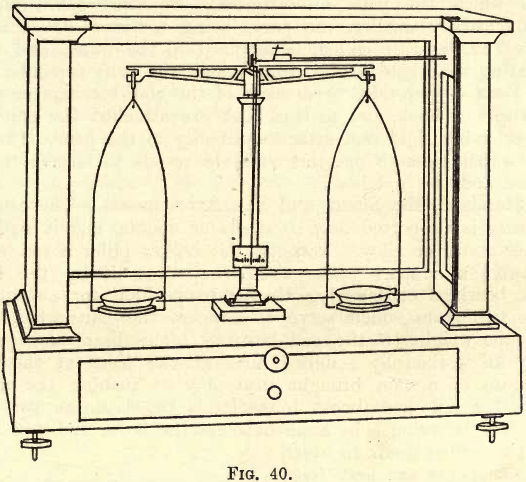
The Beam
This is generally made of brass or aluminium, and varies in shape and length. Fig. 40 shows one design (Ainsworth, U.S.A.). A short beam is preferable to a long one, the time of vibration being shortened, and the increased lightness permitting higher sensibility. One end of the beam is always graduated, though it is advisable to have both ends graduated, each into 10 divisions marked 1, 2, 3, … 8, 9, 10. Each of these divisions is again divided into five parts. Other graduations are met with, and the student, when he meets with them, must find their value in terms of the pan weights (see the following). Attached to the beam is either a small movable vane on the top edge, at the centre, or one or two movable milled heads, working along horizontal screws, on the extremities of the beam. These devices are for the purpose of altering the centre of gravity of the beam in a horizontal direction, thus causing it to swing at will more one way than the other. Attached to the centre of the beam by a small bracket is a long pointer, at right angles to the length of the beam, and pointing downwards. The fine extremity of this pointer passes in front of a small ivory scale, graduated on each side of the centre into ten equal parts, as in fig. 41.
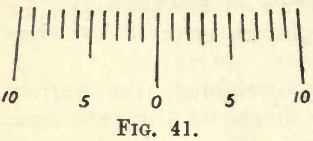
The use of this scale will be seen under “Methods of Weighing.”
On the beam are three bearings—one at the centre and one at each end. The centre bearing, on which the beam swings, consists of a triangular prism of steel or agate, attached to the beam by one of its faces, with its free edge bearing on a flat agate plate on the top of the standard. The end bearings, to which the pans are attached, are somewhat similar in construction, but usually smaller, the parts being reversed—i.e. the prisms or “knife edges,” as they are called, being fixed in the beam, and their upper edges supporting the agate planes, from which the pans depend.
The Pans
Suspended from each of the end bearings as described is a small stirrup and hook, and to this hook are attached the pan suspenders, which are preferably rigid and attached directly to the pans. On these pans are placed “ watch glasses ” or other suitable vessels to receive the substance
to be weighed and the weights.
The Standard, the Beam, and Pan Arrestments
The centre post on which the beam is supported may be single or double, and is made of hollow brass or other metal or alloy. Through the hollow pillar a rod works which raises or lowers a support under the beam, thus lifting the knife edges off the agate bearings or lowering them into position for swinging. Under the pans are two stops which serve to support the pans when not in use and to take the weight off the end bearings. The beam and pan supports are generally all worked by a milled head at the front of the base of the case. By means of a cam brought into play on turning the milled head, the stops are lowered and almost immediately the beam support drops and the beam is free to swing. In some balances the beam and pan motions are operated by two milled heads, in which case the pan supports are first freed and then the beam support.
The Case
This is generally of mahogany with glass sides, front, back and top, and plate-glass base-plate. In front is a sliding door, and below are two small drawers for the necessary accessories. At the sides are the arms for operating the rider on the beam. When not in use the case is closed and carefully enclosed in a dust-proof cover of green baize with Mackintosh lining. The balance table must be solid and free from vibration, and the balance beam must be well lighted.
The Weights
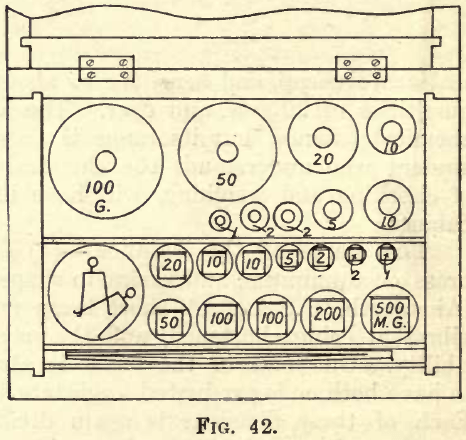
It is advisable that the metallurgical student purchase a set of weights for his own use. A set costing about £3 will, with care, last a lifelime, and if made by such firms as “Oertling” or ‘‘Becker & Sons,” they can be relied on for accuracy (see fig. 42). A set ranging from 50 grams to .001 grams with riders will answer all purposes. The brass weights in the box give the grams; the larger foil weights, marked either .5, .2, .2, .1, or 500, 200, 200, 100, give the decigrams, and the smaller foil weights, marked .05, .02, .02, .01, or 50, 20, 20, 10, give the centigrams. Many sets of weights include still smaller foil weights, but these are superfluous, as the milligrams are obtained by using the rider on the beam, the whole numbers on the beam representing milligrams when the rider weighs one centigram and the beam is divided into ten equal parts. Fractions of a milligram are read from the subdivisions between the whole numbers. Some makers subdivide their weights thus: 10, 5, 2, 1, 1, 1; some thus: 10, 5, 2, 2, 1; and some thus: 10, 5, 3, 2, 1, and so on. The weights are handled by the forceps provided.
Methods of Checking the Accuracy of the Balance & Weights
When obtained at a fair price from a good maker, the balance and weights are generally sufficiently accurate for the student’s purpose ; but, in order that he may gain an insight into the principle of the balance and the magnitude of error (if any) that may arise from defects in the balance and weights the Ostwald’s incomplete scheme is laid down. (For fuller information consult following Physico-chemical Measurements.)
Checking the Balance
Having seated himself on a stool of convenient height, the cloth cover is removed and the student is ready to test the accuracy of the balance, his note-book and set of weights being at his hand. See that the balance is level, adjusting, if necessary, the base thumb-screws. Gently turn the milled head and release the beam, so that it swings four to five divisions right and left on the pointer scale (that is, about half-way across). When reading this scale keep the eye opposite the zero point in all cases. If in proper order, the pan stops should drop just slightly ahead of the beam rest and the beam should swing gently. The whole movement must be gradual and without any sudden jerk. (If unsatisfactory, refer the matter to the demonstrator; do not at present attempt to rectify it without aid.)
If the beam swings more to one side than the other, arrest it. Then, with a broad camel’s-hair brush, carefully dust the pans and top of the beam. Again try the swing, and if no better, then adjust it by slightly moving the centre vane towards the lighter side, or by moving the end screw towards the lighter side. Try the swing, and repeat till the centre of the swing is one division from the centre of the scale. If, for instance, the pointer swings four right and three left, it will come to rest at +1, or the centre of the swing is one division to the right.
The student will now proceed to test:
(a) The Sensitiveness of the Balance under Different Loads. —Release the balance to swing between +6 (on the right) and —6 (on the left). To aid the swing open the door and gently fan one pan with the hand till the desired motion is obtained. Close the door. Note three consecutive swings,
say—

The average of the left swings is 5 + 4.5/2 = 4.75, therefore the centre of swing or deviation with empty pans is +6 — 4.75= + 1.25 or 1¼ divisions to the right. By care the student may approximately subdivide each scale division into quarters.
With a good balance the swing should diminish very slowly thus: — 6, + 5; -5.75, + 4.75; -5.5, + 4.5, and so on. If the swing drops off suddenly, thus : – 6, + 5 ; — 5, + 4 ; – 4, +3, and so on, unscrew the small bob on the pointer and raise it about half an inch. Fasten. Swing and note the effect. The swing should be slower and should drop off more gradually, the centre of gravity of the beam having been raised. The centre of swing may be slightly altered, and, if so, is brought back again by the vane as before.
These preliminaries being satisfactory, the student will now ascertain the effect of adding 1 mgm. by means of the rider in each of the four following cases:—
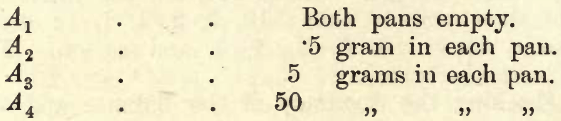
A1. Both pans empty.—As before, find the deviation of swing without the rider on the beam, say—

Now, place the centigram rider on the 1 mark on the right-hand end of the beam. Note the swings, say—

Therefore 1 mgm. causes a deviation in the swing of the pointer of .87 + 1.13 = 2 divisions on the scale. This shows the sensitiveness of the balance unloaded. If the pointer bob be raised, the sensitiveness is increased; if lowered, it is diminished.
A2 In each pan place .5 gram (using, if necessary, weights from another box). Remove the rider and find the deviation. Remove the rider at the 1 mark and, as before, find the total deviation for the 1 mgm. overload. Note the results.
A3. Proceed as in A2, but with 5 grams in each pan.
A4 Proceed as in A3 but with 5 grams in each pan.
Tabulate the results thus:—

The figures given throughout are imaginary, but with a good balance, through the range given, the sensitiveness should drop off but very slightly.
(b) The Equality of the Arms of the Balance.—In each pan place 50 grams. Take the deviation. Reverse the loads, placing the right hand weights in the left hand pan and the left hand in the right pan. Again take the deviation. If the arms are of equal lengths the deviations should be equal and opposite. A knowledge of the ratio of the arms is only necessary in correcting the weights when a high degree of accuracy is required (see method of checking weights given in “ Ostwald ”), and if weighings are made by substitution no error can result from inequality in the lengths of the arms and by the direct method of weighing; if the weights be always placed in the one pan the relative weights will be correctly given.
In the weighings just performed the student should note whether the deviation for empty pans (without the rider) is constant. It must not vary once it is adjusted. If it does so the fault generally lies in the knife edges, and can be remedied only by the maker.
Checking the Weights of a Balance for Calibration
Various methods have been laid down for checking sets of weights. The method given by Ostwald takes into account the length of arm of the two sides of the balance. The following substitution method is convenient, simple and accurate, giving the relative values of the weights. One weight, say 0.01 gram, is assumed to be correct, and the relation of the other weights to this ascertained by counterpoising this weight placed in the right-hand pan (r) by a weight from another box in the left-hand pan (l). The .01 weight is then removed and replaced or substituted by the other .01 in the set, and its value is ascertained. The first steps are here worked out in detail, and then the whole procedure is tabulated. The set of weights here taken runs 50, 20, 10, 10, 5, 2, 1, 1, .5, .2, .1, ‘1.05, .02, .01, .01, and the rider .01 (R).
First Step
To check the two .01 Weights and the Rider.—Mark one of the .01 weights by turning up one corner. Place it in the r.h. pan and counterprise it with a .01 weight (from another box) in the l.h. pan. Note the deviation, which should be between +1 and – 1 if the balance was in adjustment with empty pans.
Remove the .01 gram and replace it by the second one from the set, leaving the counterpoise in the l.h. pan. Again take the deviation. For example, suppose the deviation with the first .01 is + 1 and with the second .01 is + 1.25.
The second weight is lighter than the first by .25/2.00 mgm., provided an overload of 1 mgm. corresponds to 2 divisions on the pointer scale. Then the true weights are No. 1, .01 = .01 gram. No. 2, .01 = .00988 gram.
Then take the .01 gram rider and find its deviation against the same counterpoise. Suppose the deviation now is +.75. The rider then is heavier than the first .01 weight by .25/2.00 mgm. Therefore its true weight, compared with No. 1, .01 = .01012 gram, we have now.
True weight No. 1, .01 weight = .01 gram (assumed)
True weight No. 2, .01 weight = .00988 gram (assumed)
True weight No. Rider, = .01012 gram (assumed)
Second Step
To check the two .02 gram weights.—Place the two .01 weights on the r.h. pan and counterpoise with weights from the other set. Note the deviation. Remove the two .01 weights from the r.h. pan and replace them by the .02 gram weight. Note the deviations. Suppose with the two .01 weights the deviation is + .5 and with the .02 weight it is + .3 (as nearly as can be read), then the .02 weight is heavier than the two .01 weights by .2/2.00 mgm.
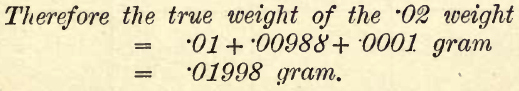
The subsequent steps are worked out in the same way, and are indicated in the following tabulation, which, when fully worked out, will show the true values of the different weights.
NOTE.—To distinguish the two 1 and the two 10-gram weights, advantage must be taken of some slight difference in the marking or shape of the weights.
Only the details of steps I. and II. are fully tabulated. In the column “Weight Tested and Substitution” the weights substituted are in small print and weight tested in bold type. Generally the weights supplied by good makers will be found to be correct to a small fraction of a milligram, and can be used in analyses without correction. In any case the student will find the total error involved by adding up the corrected values of the weights and comparing this sum with that of the nominal values of the weights used.
Analytical Balance Instructions Guide
The observance of the following points will secure good results:
- See that the balance is level (notice the levels).
- See that the pans and all parts are clean.
- All movements must be gentle.
- Never touch the weights with the fingers.
- Always place the weights on the right-hand pan.
- Always use the arrestment when changing weights or rider.
- When arresting the beam the pointer should be about the zero mark on its scale.
- Always close the door when using the rider.
- Never place a substance directly on the pan. A watch glass or other vessel must be used.
- All apparatus placed on a pan must be absolutely dean.
- Never weigh a piece of apparatus when at a much higher or lower temperature than that of the balance.
- Hygroscopic substances should he weighed in closed vessels.
- Always note down the weights used before removing them from the pan, and check the total weight by reading the blank in the box. Remember to remove the rider.
These instructions are sufficiently comprehensive, and the student must impress them on his memory. Each instruction has its definite value, and should not be passed over superciliously as a needless refinement. Carelessness on such points, besides giving inaccurate results, will, in his future career, call for remark: an employer may safely assume that a chemist careless in weighing will be careless in other operations, and will value his services accordingly.
Methods of Weighing
In the following instructions several methods are given for the purpose of widening the student’s knowledge of the subject. Some of these methods, he will see, are unsuited to the requirements of everyday routine work where speed is an essential. The methods here taken are as follows:
Determination of the Apparent Weight
(1) By Direct Weighing
(a) By Vibrations.
(b) By the Rider (without calculation.)
(2) By Substitution.
Determination of the Absolute Weight
A. (1) The Apparent Weight by Direct Weighing.—(a) By Vibrations.—Assuming that the weights have been, checked amongst themselves as before described, and their true weights in relation to each other (relative weights) determined, the apparent weight of any substance is obtained by counterbalancing it with these weights. No allowances are made for buoyancy of the air, nor are the weights compared with the standard of mass (a cylinder of platiniridium kept in Paris, the mass of which is called 1000 gm. or one kilogram). In all analytical operations the apparent weight only need be determined.
It is assumed as an example that the weight of a platinum crucible is required. Three operations are necessary.
- Take the deviation with empty pans. Call this e.
- Place the crucible on the l.h. pan. On the r.h. pan place 10 gm. Release the balance gently. If too light add the other 10 gm. Again release. If too heavy, remove, and try the 5 gm. in place of one of the 10 gm. weights.
If now too light add the 2 gm. weight and so on, always systematically replacing a weight that is too light by the next heavier, and one that is too heavy by the next lighter until the foil weights in the second decimal place have been used. Say the weights on the pan are 10 +5 + 1 + .2 + .1 + .01 = 16.31 gms. If another .01 is too much, place the rider on the beam and move it along systematically till equilibrium is nearly attained. Say with the rider at the 4 mark the weights are too light, and at the 5 mark too heavy. Then place the rider on the 4 mark and take the deviation. Call this deviation 1 (light).
3. Now place the rider on the 5 mark and again take the deviation. Call this deviation h (heavy).
The crucible weighs between 16.314 and 16.315 gms. Apparent weight then = 16.314 + l – e/l – h mgm.
Assume that e (empty pans) = +6
l (16.314) = +12
h (16.315) = -5
Apparent weight = 16·³ 14 gm. + 12 – 6/12 – 5 mgm.
= 16.314 gm. + 6/17 mgm. (.35 mgm.)
= 16.31435
Exact weighings by this method should only be made when it is certain that the object to be weighed is accurately defined down to tenths of a milligram. This case is rather rare. Vessels of glass, platinum, or other metal may change in weight whole milligrams according to the moisture in the atmosphere, therefore it is waste of time weighing to tenths of a milligram when the milligrams are doubtful.
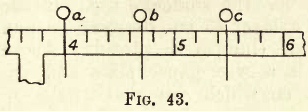
(b) By the Rider without Calculation. — By means of the vane adjust the balance so that the pointer swings equally on both sides of the zero mark. Proceed as before to add weights to the pan till the crucible is approximately balanced. Close the door, and with the rider arm move the rider till nearly at the correct spot. Release the balance. Note the swing. If more to one side than the other, arrest and move the rider a little at a time, repeating till the pointer moves evenly on each side of the zero mark. Assume that the rider lies as shown in fig. 43.
Then the weight of the crucible will be 16.3140 gms., with the rider at a, 16.3147 gms. at b, and 16.3155 gms. at c. With practice this operation can be very quickly performed, the left hand working the milled head and the right hand the rider arm.
This method is sufficiently accurate for all the work in this section, and will be found the most convenient and rapid. When performing a series of weighings the balance should be checked every now and then to see that the pointer swings evenly on each side of the centre. When noting down the weights add them up mentally as follows:—(10 + 5 + 1 = 16), (.2 + .1 = .3), (.01), (Rider .42), total 16.3142. Also when returning the weights to the box add up mentally the empty spaces as a check on the former addition.
A. (2) Weighing by substitution.—The previous methods give good results provided the balance (as is generally the case with good makers) be well designed. In the method to be described good results may be obtained even with a very inferior balance.
Place the crucible (or other object to be weighed) on the l.h. pan. On the right-hand pan place a watch glass, and with a small spatula place on it some litharge (or other heavy powder), adding or deducting a little at a time till the crucible is approximately counterpoised. Obtain exact equilibrium by a rider on the right-hand end of the beam. Now remove the crucible and in its place put weights from the box till equilibrium is again obtained, using a rider on the left-hand end of the beam.
Note the weights thus used. Then if these weights are correct (or are checked as before by substitution) the true apparent weight is thus obtained.
Determination of the Absolute Weight
For fine weighings such as are required in certain physical measurements allowances are made for the different densities of the various weights and the substance weighed. The weights again have to be checked, not only amongst themselves, but also must be compared with the standard of mass. For this purpose it may be taken that 1 cubic decimetre of water at 4° C. weighs 1000.013 gms.
As these matters relate more to Physics than Chemistry the student is referred to Elementary Practical Physics, by Stewart and Gee.
Apparatus used in Weighing
The student will find it convenient to procure or prepare a pair of counterpoised watch glasses about 6 cm. in diameter; or he may take a single watch glass and prepare a counterpoise from a piece of brass by filing. If accurate within a milligram, the final adjustment may be made with the rider. When required to weigh out some quantity of a powder he places the watch glass on the l.h. pan and the counterpoise on the r.h. pan Then with a spatula or from any vessel he adds to the watch glass some of the powder and ascertains its weight. Special care must be taken that none of the powder falls on the pan.

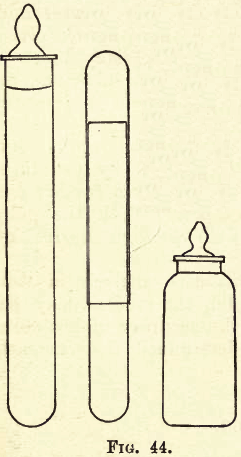
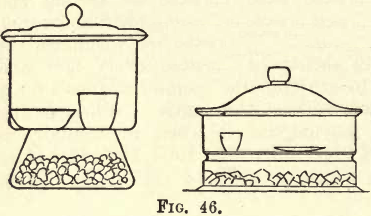
Fig 44 and fig. 45 show three forms of weighing bottles and a pair of watch glasses in a clip. These are used for hygroscopic substances (which absorb moisture from the air and will be referred to further on).
Fig. 46 shows two forms of desiccators, the left-hand one being more convenient for the student’s use. In the lower part of the desiccator a layer (3 cm. deep) of calcium chloride (lumps) is placed. Above this is a wire gauze plate and triangle on which rest the articles to be desiccated or dried. The joint of the cover and body is accurately ground, and should be neatly smeared with vaseline. The calcium chloride being a strong absorbent of moisture, rapidly dries any article placed on the gauze, and as the lid is air-tight, moisture cannot enter from the outside atmosphere.
Quantity of Material to be Weighed Out
This is generally based on the quantity (supposed to be present) of the substance sought. Where this is approximately known .3 to .5 gm. will be sufficient if the substance sought is present in fairly large proportion, say over 20 or 30 per cent. If only a few per cent., then 2 or 3 gms., and if fractions of a per cent. 5 gms. or more.
This, of course, presupposes knowledge that the student frequently does not possess. If, then, he has nothing whatever to guide him, let him take about 1 gm. and run a trial. Then, if he finds only traces of the substance sought, he must take a larger quantity, say 5 gms., or if he finds a high percentage he may take .3 to .5 gm. He must so regulate the quantity that the precipitates obtained are not too bulky. A large precipitate is difficult to wash, dry, and ignite, and again, on the other hand, with a very small precipitate the manipulation losses are proportionately greater and cause serious error. The happy mean must be struck, and the figures given afford some clue as to the right proportions. Never, unless specially directed, weigh out exactly 1 gm. or .5 gm. or other exact weight of a substance, as the final adjustment of such a weighing takes much time. Add the powder approximately, and then ascertain the weight taken, say .9982 gm. or .5120 gm., etc. This involves a little extra time in calculating the results, but with the aid of logarithms this is more than counterbalanced by the time saved in weighing. Examples of these calculations will be given further on. These remarks only apply to the delicate chemical balance. With the pulp scales large quantities can be weighed exactly with a high degree of accuracy.
In some of the preliminary exercises in quantitative analysis in this section, instead of taking a weighed quantity of a solid, the student may be given a certain volume of a checked solution, and the accuracy of his work is checked by the demonstrator, who has carefully determined the contents of the solution (in bulk).
