Much of Basic Geological Survey Methods consist of calculating areas.—To find the distance from an inaccessible place. —To solve problems in connection with adits, shafts, lodes of a mine.—Position of a shaft with regard to a lode.

In ordinary surveying, a Gunter’s chain 66 feet long, and consisting of 100 links, each tenth one of which has some distinguishing mark attached, is very frequently used for measuring lengths. When the number of square links in a piece of ground is known, this divided by 100,000 (the division being performed so easily by striking off five figures from the right hand side to the left) will represent the number of acres in the area.

To find how many acres there are in a rectangular piece of ground, multiply the length in links by the breadth in links, and divide the result by 100,000.

Example.—Find the area in acres of a rectangular piece of ground, the length of which is 1,225 links (that is, 12 chains and 25 links), and the breadth 150 links (that is, one chain and a half).

The number of roods in the .83750 of an acre may be found by multiplying this by 4 and dividing by 100,000 ; the number of poles, by multiplying the remaining decimal by 40 and dividing by 100,000. Thus :—

Therefore the whole area = 1 acre, 3 roods, 14 poles.

To find the area of a triangular piece of land, find the area of the triangle in square links and divide by 100,000.
To find the area of a triangle in square links, multiply the length of the base by the length of the perpendicular from the opposite corner to the base and divide the result by 2.

Example.-—Find the area of the piece of land A B C.
Set up poles at A B C. Measure B C. Travel from B towards C until a point D is reached where the line A D seems to be at right-angles to B C. Measure A D.

Suppose B C = 1200 links; AD = 168 links.

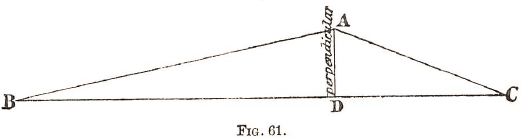
Area in acres = 1200 X 161/2 X 1/100000
which worked out as in the last example will give
1 acre, 3 roods, 29 poles.

To find the area of a piece of land indicated by the figure A D C B. Measure B D. Then find areas of triangles A D B, B D C, as in the last example.

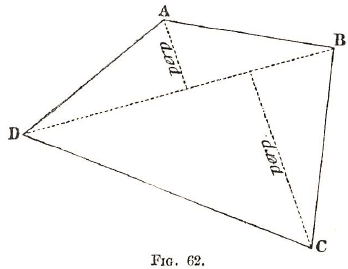
The whole area equals the area of the triangle A D B added to that of the triangle B D C.

Similarly, to find the area of a tract of land A B C D E.

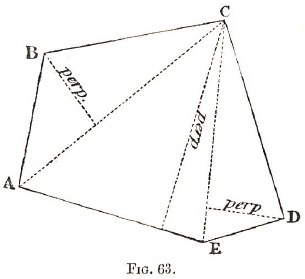
The whole area equals the area of the triangle C D E, plus that of A C E, plus that of A B C.

In any of the above calculations, should the measurement be by yards and feet, the number of square yards in the land divided by 4,840 will give the number of acres. To find the distance between the points where one is inaccessible from the other—for instance, on the other side of a river.

Required the distance between B and A.

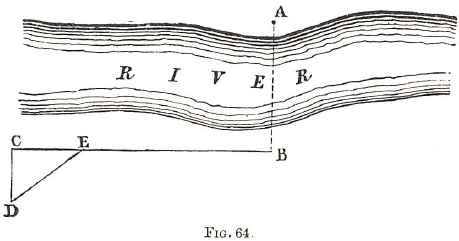
Pace off from B, at right-angles to the direction B A, a distance B E; then continue pacing off a distance E C, so that E C may be some even fraction of B E (say one-fourth or one-eighth). Proceed, at right angles to C B, along C D until a point D is reached, where D E A seem in one and the same straight line.

Then:
Required length A B = C D x E B/E C

Very frequently the prospector may wish to form some idea of the length of an adit necessary to meet a perpendicular shaft sunk from a certain known spot, or the length of a vertical shaft necessary to be sunk to meet an adit driven in from a certain point. To solve such problems (as well as many others in connection with surveying) a very limited knowledge of the properties of a right-angled triangle, together with a Table of Sines (see Appendix), may prove useful.

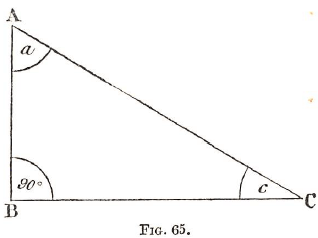
Let A B C be a right-angled triangle.

(i) Perpendicular A B equals length A C multiplied by sin c.
Base B C equals length A C multiplied by sin a.

Let A C represent two points on a hill-side, from which respectively a shaft, A B, is to be sunk, and an adit, C B, driven. Let B be the point where they may be supposed to meet. Measure length A C, and suppose it to be 200 feet. Measure either the vertical angle a (which is really 90°— the dip of the hill-side) or else the angle c, which is the dip.

Let a = 50° 30′; and c – 39° 30′.

Then by (i)—

Perpendicular A B equals 200 feet x sin. 39° 30′.
Perpendicular B C equals 200 feet x sin. 50° 30′.
Now by Table of Sines, sin. 39° 30′ is ·6361,
and, sin. 50° 30′ is ·7716.

Therefore : perp. A B equals 200 feet x ·6361.
base B C equals 200 feet x ·7716.
That is : perp. A B is 127·22 feet,
base B C is 154·32 feet.
The length of the shaft is 127·22 feet, and that of the adit 154·32 feet.

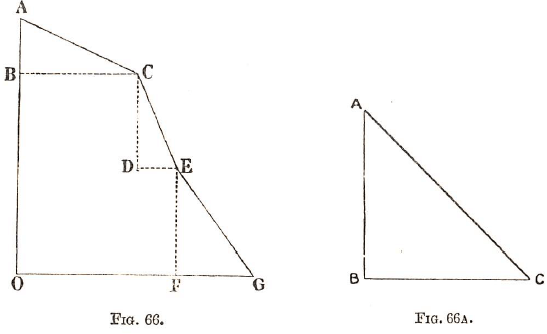
Should the hill-side A C E G be irregular, such as in Figure 66.
Then A C, C E, E G, should be measured from convenient points, A, C, E, G. To find the length of shaft A O, find the lengths of A E, C D, E F, as in the last example. The whole length A O equals the sum of the lengths A B, C D, E F.

In the same way, the length of the adit O G equals the sum of the lengths B C, D E, F G.
Also, if any two sides of the right-angled triangle A B C are (known, the third side can also be found without using the Table of Sines.

For A C = square root of (A B² + B C²)
For A B = square root of (A C² – B C²)
For B C = square root of (A C² – A B²)

Thus, supposing A C = 100 feet,
A B = 80 feet,
B C would equal the square root of 100 x 100 — 80 X 80, that is, square root of 3600, that is, 60 feet.

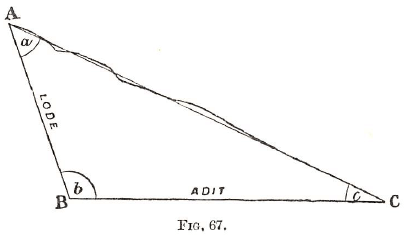
If it is required to know how deep a shaft will have to be sunk, or how long an adit driven, to strike a lode whose inclination to the hill-side is known, certain properties belonging to any triangle and a reference to the Table of Sines will suffice. Let A B C be a triangle where A C represents the hill-side, A B the lode, C B an adit. Let the length A C be known, and also the angles a and c (and therefore the angle b, which is 180° — the sum of angles a and c). Suppose it be required to know how far the adit will have to be driven to cut the lode and also the depth of the lode.

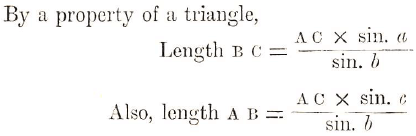
The question, Where ought a shaft to be sunk has to be decided on as soon as development work is contemplated ; and though the question depends in some measure on the nature of the country, rock, and other considerations, the following general hints may be useful.

If the lode dips in the same direction as the hill-side, the shaft ought to be as in Fig. 68, A.
If the lode dips contrary to the slope of the hill, then either the shaft should be sunk on the lode or higher up than the outcrop, or else below the outcrop, so that cross-cuts can be driven (Fig. 68, B).

In certain cases, when the lode lies at a considerable inclination from the perpendicular, the shaft should be sunk along the lode rather than in a vertical direction.

Adit levels, which facilítate the proper working of a mine, also help to drain it; and, in consequence, they should be driven at as low a level in the valley as possible, and with a very gentle slope, just sufficient to enable the water to flow away.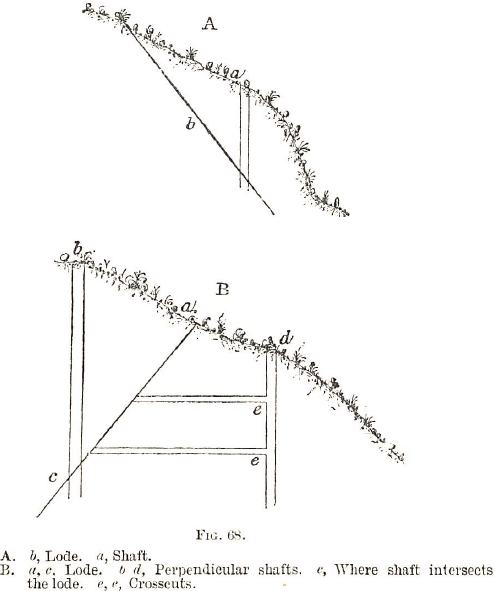

With regard to the size of shafts and adits, the dimensions of the former vary from 6 by 5 feet to 8 by 6 feet, while the engine shafts are usually 11, 12, or 13 feet by 8 feet; the adits are generally 7 or 6 feet in height, and a 4 or 6 feet in width.

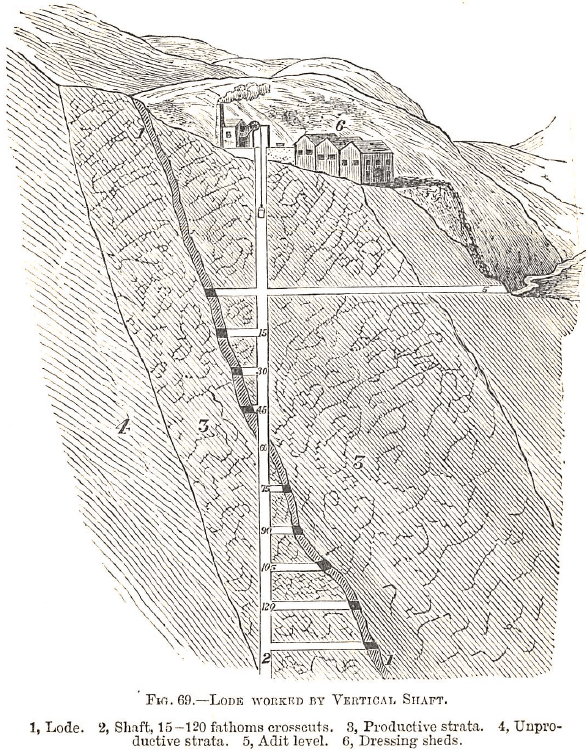
N.B.—The ore is more difficult to raise up a slanting shaft than a perpendicular one.