Calculating Stockpile Capacity: Once the minimum storage capacities which will assure maximum mill output are known, the appropriate stockpile configuration must be determined. Stockpiles fall into two general categories: conical and elongated.
Conical Stockpiles
The conical stockpile is the simplest and easiest to analyze. The total stockpile capacity is given by:
3.14 (Tan A)R³ D/3000 = capacity in metric tons…………………(1)
where: R = stockpile radius in meters
A = angle of repose for material to be stockpiled
D = density of material in kg/m³
Note that the capacity of the conical stockpile varies with the cube of the radius of the pile. This means that the capacity of the conical pile grows very rapidly as the height (and hence the radius of the pile) increases. Increasing the height of the stockpile by 26% results in a doubling of the stockpile capacity. One should also observe at this point that one-half of the capacity of the stockpile is in the lower 1/5 of the pile. This fact will become important later in considerations of live storage capacity.
For many common materials, the angle of repose, A, is about 38 degrees. Substituting this value for A reduces Equation 1 to:
8.18 x 10 -4 R³D = capacity in metric tons………………….(2)
In English units, Equation 2 becomes:
4.09 x 10 -4 r³d = capacity in short tons…………………(3)
where: r = stockpile radius in feet
d = density of material in lb/ft³
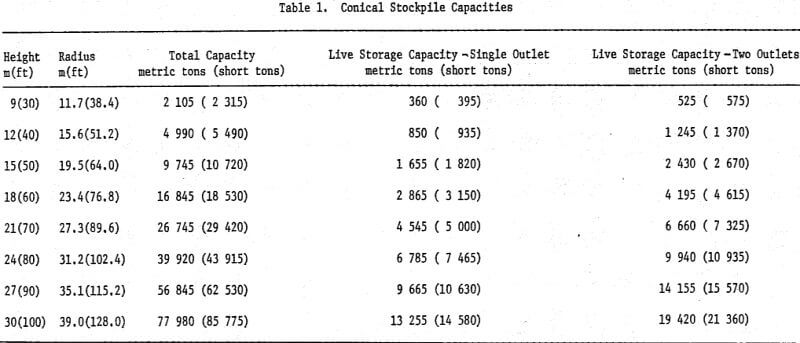
For convenience, typical stockpile capacities have been tabulated in both metric and English units in Table 1.
The main advantage of the conical pile is that it can easily be built by dozing equipment or a fixed belt conveyor. One disadvantage is that very high stockpiles are required to attain large storage capacities. This results in very long conveyors and supports and accompanying large foundations to withstand the loads on the conveyor. More importantly, because the conical pile occupies such a small ground area in relation to its volume, soil pressures on large piles can exceed the bearing strength of the local soil. For example, if 1600 kg/m³ (100 lb/ ft³) material is being stockpiled on soil with an allowable bearing pressure of 14 680 kg/m³ (3000 lb/ft³) the maximum permissible conical stockpile is about 27.4m (90 ft.) high and has a total storage capacity of about 56 000 metric tons (62 000 short tons).
Elongated Stockpiles
The elongated stockpile and its variations are the most common stockpile form in high capacity installations. The capacity of the stockpile can easily be determined by considering the pile as two separate volumes.
The end half cones can be combined to form a single conical pile which can be analyzed using Equation 1, 2 or 3 above. The capacity of the center section of the elongated pile is given by:
R²LD Tan A/1000 = capacity in metric tons………………………(4)
where: R = radius of end half cone in meters
L = length of center section in meters
D = density of material in kg/m³
A = angle of repose for material to be stockpiled
For a value of A of 38 degrees, Equation 4 reduces to:
7.81 x 10 -4 R²LD = capacity in metric tons……………………………..(5)
Equation 5 expressed in English units is:
3.91 x 10 -4 r²ld = capacity in short tons………………………………….(6)
where: r = radius of end half cone in feet
l = length of center section in feet
d = density of material in lb/ft³
The total capacity of an elongated pile is the sum of the results of Equation 1 and Equation 4. A kidney-shaped pile such as that formed by a radial stacker is merely a variation of the elongated pile. The capacity analysis is identical to that for an elongated pile except that the arc length of the center section is substituted for the value L in Equal 4 above. The arc length is given by:
3.14 (Pr)B/180 = arc length in same units as Pr……………………………..(7)
where: Pr = radius of central section peak (Horizontal distance from stacker pivot to peak of central section)
B = angle (in degrees) formed by radii at limits of central section peak
The main advantages of an elongated stockpile are that it can easily be varied to fit into a plant layout and very large stockpiles can be built without raising the ore to prohibitive heights. The main disadvantage is that the stockpile building equipment is more complex and usually requires a higher capital investment. As indicated previously, soil pressures under an elongated pile are lower than those under conical piles of equivalent capacity.
This is an important fact that should not be overlooked in the design of a stockpile system. In comparing the two types of systems, one should also always consider both the capital costs and operating expenses before deciding on one system or the other.
Calculate Stockpile Live Storage
In the discussions above, only the total capacity of the stockpiles was considered. This capacity is useful if reclaiming is done with a front end loader or if a bulldozer or bucket wheel reclaimer is used. Usually, the figure for total stockpile capacity is utilized when planning for the longest scheduled shutdown. In that circumstance, one should expect to use a bulldozer to obtain complete stockpile reclaim so that the stockpile will not be any larger than necessary. With belt conveyors in normal operating circumstances, one should work with the live storage capacity; that is, the portion of the stockpile that will flow into the feeders in the reclaim tunnels without dozing of the pile. The portion of the stockpile outside this live storage section is referred to as dead storage. Obviously, the following analysis does not apply when a front end loader is used for reclaiming. In this discussion, we will consider only a linear arrangement of outlets under a conical stockpile. Elongated stockpile dimensions and non-linear reclaim schemes are so variable that a general discussion is meaningless and each system should be evaluated individually. For the sake of comparison, the live storage capacity of elongated stockpiles is generally about 25% to 30% of the total stockpile capacity assuming a sufficient number of outlets are used. We will begin with the simplest case: a conical stockpile with one outlet at the center.
The live storage capacity of a conical stockpile with a single outlet is easily evaluated by considering what happens when one draws material out of the stockpile. Material will continue to flow to an outlet as long as the angle of the withdrawal cone is steeper than the drawdown angle of the material. Once the drawdown angle is reached, material will cease to flow to the outlet of its own accord. This drawdown angle varies from material to material but is usually about ten degrees steeper than the angle of repose for the material. In other words, if the angle of repose is 38 degrees, the drawdown angle is usually about 48 degrees. Obviously, the drawdown angle will vary depending upon the size range of the material and its wetness. If the application is critical, one should attempt to determine the drawdown angle through testing since it has a great effect on actual live storage capacity; however, for general purposes the “angle of repose plus ten degrees” rule is sufficiently accurate. If one sketches in the drawdown angle on a cross-section of a conical pile, it will be seen that the live storage volume consists of an inverted cone with an upright cone on top of it. Calculation of the volumes of these two cones for a stockpile with a 38 degree angle of repose and a 48 degree drawdown angle shows that the live storage portion of a conical stockpile with a single outlet is about 17% of the total stockpile volume. This low figure is reasonable since, as mentioned in the Conical Stockpile section above, one-half of the total stockpile volume is in the lower 1/5 of the pile and it is this section that is least affected by the single outlet withdrawal cone. For convenience, the live storage capacity of typical conical stockpiles is tabulated in Table 1.
Since the live storage portion with a single outlet is only 17% of the total volume, one could logically attempt to increase the live storage percentage by using multiple outlets. In fact, if one uses the same stockpile as above but with two outlets rather than one, the live storage portion rises to about 24.9% of the total volume which is almost half again as much as the single outlet value. The gain in live storage rapidly falls off when more than two outlets are used. When three outlets are used, the live storage portion is about 26.5% of the total volume. This is an increase in live storage of only 1.6% of the total stockpile volume. This small increase does not usually justify the expense of installing a third outlet and feeder with its corresponding reclaim conveyor and tunnel extensions. The two outlet arrangement is usually the best since it provides considerably more live storage than the single outlet arrangement and provides a backup feeder if one of the two is down for repairs. Approximately 59% of the total live storage capacity will be available if only one outlet of a two outlet system is used.
It should be noted that outlet placement is extremely critical to the attainment of the indicated live storage capacities. In the example above, if the outlets are placed 1/10 of the pile radius too close to the center of the pile, the live storage portion drops from 24.9% to only 19.3% of the total volume. This is only 13.5% more than the single outlet value rather than the almost 50% increase indicated above. The live storage capacities for typical conical stockpiles with two outlets at the “ideal” distance from the center of the pile have been tabulated in Table 1.