The usual method of sampling mineral deposits is to drill holes and assay the sludge or core. Though the results thus obtained may not represent the true average value of the deposit, it is on these results that estimates of practically all large orebodies are made. In a large number of cases, the results of exploitation fall far short of the estimated value of the orebody.

The standard method of making these estimates is to find the cubic contents of triangular prisms, in the apexes of which the drill holes are placed, by multiplying the surface area by the average depth of the ore in the three drill holes and then multiplying the cubic contents by the specific gravity of the ore or rock to find the tonnage. The assay value is found by dividing the sum of the products of the depth of ore in each hole and the corresponding assay value by the sum of the depths of the ore in the three holes. As the latter part of this method is subject to many mathematical errors, it should not be depended on. Some engineers, therefore, use a discount factor, but as this factor is either arbitrarily selected or is obtained by obscure methods, the results are no better than guesswork.

The standard method is correct when the drill holes are so laid out that the triangular prisms are equilateral in cross-section. But as ore deposits cannot always be drilled into at regular intervals and because of the human factor, if many holes are drilled, triangular prisms of all degrees of angularity are produced. In such cases it is necessary to assume that the influence of the different holes is not the same in all directions, which assumption of course is absurd.

The area of the triangular prism is usually found by scaling; an orebody of sufficient size to justify churn drilling is too large to be handled conveniently on maps having a scale larger than from 1000 to 1 to 1500 to 1 and maps of such scales cannot be accurately measured. A variable is thus introduced in the first operation. In addition, the scaling is frequently done from blueprints, which sometimes shrink as much as 4 per cent, between printing, washing, and drying. The error due to scaling may be eliminated by surveying the location of each hole and calculating its coordinates; then from these coordinates calculating the length of each line connecting two drill holes.

For this work a rather simple formula has been derived from the regular a sin B = b sin A formula.

By subtracting the corresponding coordinates of two holes, the latitude and departure of one from the other is found. As this latitude and departure represent a right triangle and as the sine of 90° is unity, the logarithm of which is 0, the formula a sin B = b sin A may be solved and written

a = b/sin B

in which a = required distance; b = lesser remainder from subtraction of coordinates; B = angle opposite b.

When the different distances between the various churn drill holes have been found, by the regular formula for the area of a triangle

area = √s(s-a) (s-b) (s-c)

the horizontal area of the triangular prisms may easily be calculated.

In actual practice, it will not be necessary to write out any of the factors other than a, b, c, and s, the subtractions and the logarithms. When the area of the prism is thus found, it may be checked fairly closely by scaling a map kept at hand for the purpose, but this check will generally not come out as close as 1 per cent. This method does not take into consideration the fact that, in drilling, the holes may have drifted from the vertical line, thereby increasing or decreasing the actual volume of the prism as depth is attained, but neither does the scaling method.

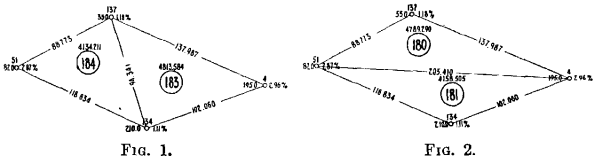
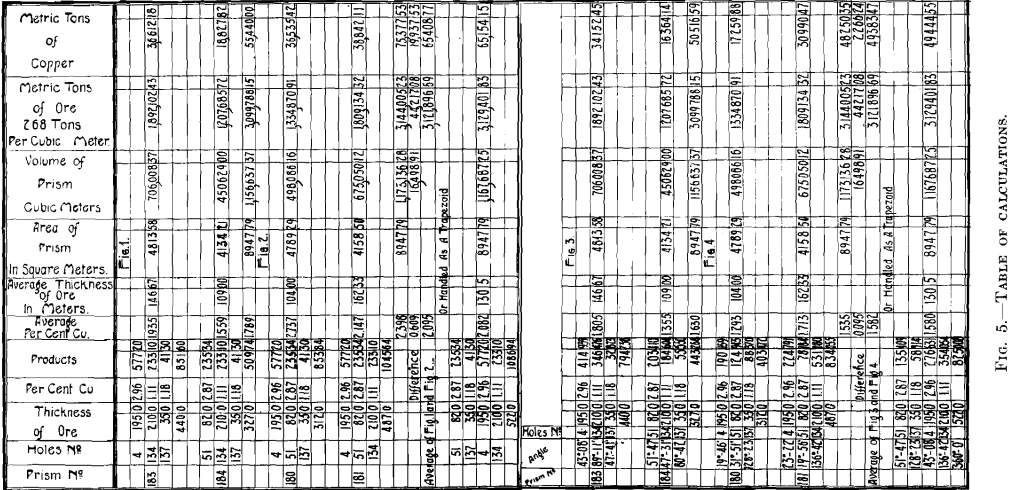
The unreliability of the standard method of calculation is illustrated by Figs. 1 and 2 which show a trapezoid having in the apexes four holes. Hole 51 had 82.0 m. of ore averaging 2.87 per cent, of copper; hole 137 had 35.0 m. of ore averaging 1.18 per cent, copper; hole 4 had 195.0 m. of ore averaging 2.96 per cent, copper; and hole 134 had 210.0 m. of ore averaging 1.11 per cent, copper. The position of these holes and the corresponding depth of ore and average assay value are given on the figures.

In Fig. 1, the trapezoid is divided into two triangular prisms of scalene cross-section, prism 184 having in its apexes holes 61, 134 and 137 and prism 183 having in its apexes holes 4, 134, and 137. The area of each prism, which is given in the figure, was calculated by the method just outlined and the results of the calculation of tonnage and grade of the ore content are shown in the accompanying table of calculations. When the trapezoid is divided in this way the two prisms contain 3,099,788.15 metric tons of ore with a metallic content of 55,440.00 tons of copper, or a grade of 1.789 per cent.

In Fig. 2, the same trapezoid is divided in the other possible way: prism 180 having in its apexes holes 4, 51, and 137 and prism 181 having in its apexes holes 4, 51, and 134. When thus divided, the table of calculations shows that the two prisms contain 3,144,005.23 metric tons of ore carrying a metallic content of 75,377.53 metric tons of copper and an average grade of 2.398 per cent.

Thus, the calculations of amount of copper in the one block of ground, when divided in different ways, instead of agreeing, differ by 19,937.53 metric tons, while the grade differs 0.610 per cent., the second calculations showing 35.63 per cent, more copper than the first. This difference is far more than is permissible, but as far as the calculation goes the one is as correct as the other, if the standard method of calculation is assumed to be correct.

Obviously when two calculations of the same mass, by the same method, show such a large difference and it is known that no mathematical errors were made, one is justified in suspecting that both results may be wrong and that the method is the probable source of error. An effort

has, therefore, been made to devise a method that will give results that will check more closely. From the beginning, it was evident that some factor of correction must be derived.

It is permissible to assume that the importance of a hole in the prism varies as the angle of which it is the apex varies from 60°; that is, if the angle is greater than 60° the importance of the hole should be increased and if the angle is less, the importance of the hole should be diminished ; or

x/Average assay times depth of ore = angle at hole/60°

in which x = importance of hole.

Solving this proportion gives the applied factor of correction which is substituted in the calculations of grade for the product of the depth times the average assay value as in the standard method of calculation.

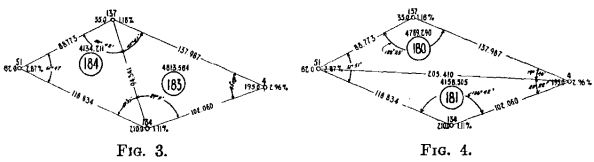
As a test, this method is applied to the same trapezoid that was calculated in Figs. 1 and 2; Fig. 3 corresponds to Fig. 1 and Fig. 4 corresponds to Fig. 2. In both cases the prisms are identical, but in Figs. 3 and 4 the angles at the holes are given.

The table of calculations, Fig. 5, shows that in Fig. 3, hole 4 has a product of 414.939 instead of 577.20 as in Fig. 1. This product is the result of solving the proportion

x/577.80 = 43°8’/60°

43° 8′ being the angle at hole 4. Each of the other holes is treated in the same way and the corrected products are used in determining the average grade of the prism. In Fig. 3, this method gives the content of the trapezoid as 50,515.59 metric tons of copper or an assay value of 1.630 per cent, copper. In Fig. 4, this method gives the trapezoid a content of 48,250.35 metric tons of copper, or an average grade of 1.535 per cent., an assay difference between the two of 0.095 per cent, as against a difference of 0.609 per cent, when the prisms were calculated by the standard method. Now 0.095 per cent, represents 1.92 lb. of copper per ton and 0.609 per cent, represents 12.2 lb. of copper per ton.

As a further check on the method, the trapezoid was calculated as one mass using the standard method as well as the method outlined; these results also are shown in the table of calculations. The closeness of the check to the average in both cases is worthy of note: by the standard method there are three results, no two of which are close enough to be satisfactory, while by the method devised none of the results differs from the others enough to cause any trouble. In this latter case, the angles were taken as proportional to 90° instead of to 60°.

From the way these drill holes, assay values, and prisms were selected, the method advocated produces a result less than the standard method, but a case could be selected, just as easily, in which the results would be be greater. In case hole 4 should fall at the location of hole 134 or 137, which have angles greater than 90°, the result would be to increase the average assay of the trapezoid. From this, it seems that the standard method is equally liable to err in being too low or too high in different cases.

Probably in calculating an orebody by the standard method the error of the calculated from the actual would not be as great as the off-check between Figs. 1 and 2 on account of compensating errors. Neither in general churn drilling would many prisms develop as scalene as in Fig. 2, but it seems that a method should not be used that can give results that vary as much as the difference between Figs. 1 and 2 when a method is available which checks as closely as do Figs. 3 and 4.

ORE RESERVE CALCULATIONS

The method referred to as standard is simply one combining mathematical calculations with judgment. Textbooks advise that care be exercised that the triangles do not center unduly around any one hole in an area divided by a series of irregularly placed holes. The author, by applying as factor the amount of spread of the angle of each triangle until he gets around the whole 360 degrees, automatically balances the proper proportion of each triangle to the area surrounding the hole.

In his description of the standard method, the author does not call attention to the fact that it is the custom of engineers to use their judgment in arranging the triangles so as not to lay improper emphasis on a particular hole, as brought out in the author’s illustration. In other words, the old method required a reasonable amount of judgment in the division of the area. The new method requires no judgment in making the area divisions. It mathematically applies a proper balancing factor regardless of the arrangement of triangles and is therefore an improvement.

The method proposed is an improvement for the mathematical calculation under the particular conditions where more desirable data are not available. The result of the calculations would be acceptable if the nature of the deposit is disclosed by the holes under consideration, otherwise it would be desirable to have additional holes at doubtful points.

It would seem that in averaging a mass, the more samples taken the better the average is liable to be. Sampling in gold mines is generally somewhat different from the sampling of large masses of ore in base-metal mines. Though the reefs or ledges are small, comparatively, there is usually opportunity to sample numerous cross-sections. On the “Rand” levels were run 100 ft. apart, and average samples taken across the ore every 5 ft. These samples were marked on the assay-plan as a fraction, the numerator representing the pennyweights and the denominator the width in inches. A block was considered developed only when its periphery had been so sampled. In the case of large orebodies and a few samples, a factor of safety would seem advisable. In a multitude of samples there is of course greater accuracy whether they are located at the apexes of triangles, or the center of rectangles.

The method extensively used in the Joplin and Wisconsin zinc districts was developed because of the extreme irregularity of the orebodies. The drill holes are spotted rather irregularly and adjacent holes are connected by straight lines. Each of these lines is bisected and a perpendicular line is drawn; a polygon bounded by these perpendicular lines is considered as the area of the ore controlled by one drill hole. The blocks of ore thus formed are calculated on the basis of the one drill hole. In that manner the whole orebody would be calculated. Some of these orebodies would be small, some would be large, but no one drill hole would influence the calculation of any ore excepting the ore immediately surrounding it.

The orebody on which I used this method contains several hundred million tons of ore, and several systems were used to estimate the copper content, viz., the so-called “standard” method of prism calculation; a planimeter method for obtaining areas, checked by logarithms; the Harding angular system of prism calculation, and a very complicated geometrical consecutive method, whereby all the totals of each hole in each prism was carried right through to the last hole. The total copper content, in tons, was then divided by the total tonnage of ore to give the copper per cent, per ton. This latter system is too laborious and tedious for general use, and was used only to check the other methods.

The results showed that the Harding angular system, as modified, checked with the geometrical system to within 1.61 tons of ore in several million tons, and the copper content to 0.00000001 per cent, per ton. The first, or “standard,” system, when checked with the geometrical, showed a variation of 138,000 metric tons and a loss in copper content, as calculated, of 0.025 per cent, per ton; the same assay data were used in both cases. The planimeter method for obtaining the total area, in this instance, varied so little from that obtained by coordinates and logarithms as not to cause any trouble at all.

The increase in the tonnage of copper by the Harding angular method proved to be more than 54,000 metric tons, and the percentage of copper per ton was also increased by 0.024 per cent.

I worked out all the prisms, about 300, by the Harding angular method and by the standard method, and checked the results in each case by the geometrical method. My calculations were then checked by others and no variation from the figures given were found. It would seem, therefore, that when one considers the numbers of times in which the calculations automatically check themselves when using the Harding system, that this system as modified, is the most reliable. The angles at the three holes must total 180°. The total products of the three holes must total 1,000, the three areas must check up with the area arrived at either by planimeter or logarithms, and the total volume must agree with the mass total tonnage when multiplied by the specific gravity, etc.

Since this system of prism calculation was published, I have had an opportunity to apply the system to an asymmetrically drilled orebody, during which some unexpected errors were found. For instance, when a prism apexed on a hole having a zero value, in several instances, the calculation showed ore of a higher tenor than any of the samples from the holes at the corners of the prism; thus, it would seem that there are cases in which the method of calculation advocated is incorrect. To take care of such cases, the following modifications have been devised:

MINERAL ORE RESERVE Case 1

When all holes have positive values, let a, b and c, be the depth of ore in the three holes forming the prism; to find the average depth of the ore influenced by any given hole, use the formula:

d = 4a + b + c/6

Then, as one proceeds from hole to hole, b and c should be substituted, thus:

4b + a + c/6 and 4c + a + b/6,

which will give the average depth of the ore in each hole. These formulas are derived as follows:

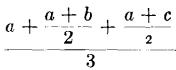
which, in reality, divides the prism into three prisms.

The area influenced by any given hole is found as follows: (1) Divide angle at hole by 180°. (2) Multiply total area of entire prism by above result. (3) Multiply area found by (2) by the average thickness (found by solution of the formula) of ore in the hole, which thus transforms this smaller prism into volume. (4) Multiply this volume by specific weight of ore, which gives total tonnage of ore in minor prism. (5) Multiply total tonnage of ore in minor prism by copper per cent, in hole, which gives total tonnage of copper in each minor prism.

After treating each hole in the prism in this manner, add the tonnages of ore and the tonnages of copper in each of these minor prisms, which will give the mass tonnage of ore and the mass tonnage of copper in the larger prism. Then, divide the mass tonnage of copper by the mass tonnage of ore, to obtain the correct percentage of copper in the larger prism. The accompanying table shows this complete calculation, which seems to leave no possible room for variation or error.

MINERAL ORE RESERVE Case 2

When one of the holes in a prism has a zero value, the same formula in the form d = 3a + b/6 is used. For finding the depth of ore influenced by the two holes having values and the percentage of area influenced, the angle at a given hole, containing ore, is divided by the sum of the two angles of the holes in which there is ore.

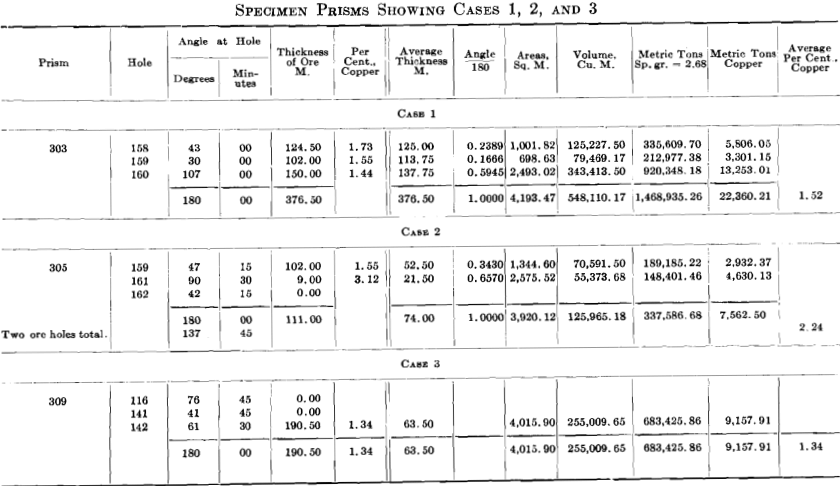
MINERAL ORE RESERVE Case 3

When two holes in the prism have a zero value, the average thickness becomes a/3, and the tonnage of ore and tonnage of copper is found by treating the entire prism as a minor prism.

In the discussion, undue emphasis was laid on the matter of “judgment,” but judgment that cannot be proved mathematically does not deserve the name of judgment. The matter of apexing prisms on holes already drilled cannot be done at will, and if an orebody is drilled in any other way than at the apexes of 60° triangles, asymmetrical prisms must result, and in plotting such prisms a person must use his judgment. In applying this system to an orebody recently, I found that, in spite of using all the judgment possible, in some cases eight prisms would have to apex at a hole having a higher grade of ore than the average and, in other cases, not more than four prisms were compelled to apex at a hole having a variation from the average grade. As a result, in some cases my calculations were unduly assisted to a higher grade, and in others unduly diminished, which was the reason for this attempt to devise a method that would not be subject to either “judgment” or accident. The results of carrying out this method through a complete orebody of a large tonnage seem to justify the labor involved therein—the tonnage checks with the standard method to within 1.014 per cent.—the standard method showed about 55,000 metric tons less copper and the percentage, by the standard method, was about 0.0242 per cent. less. This is quite a valuable consideration in the case of an orebody of several hundred million tons.