Table of Contents
- Cobalt Sorption Studies
- Description of the Ion-Exchange Resin
- Description of the Solution
- Determination of the Equilibrium- Loading Isotherm
- Cobalt Sorption Kinetics
- Resin-Fluidization Studies
- MCIX Column Modeling Studies
- Mathematical Basis For The Model
- Modeling Algorithm
- Dynamic Behavior Of The Mcix Column
- Comparison of Model Predictions To Mcix Column Data
- Predicted Optimum Operating Conditions
- Predicted Cobalt Extractions and Resin Inventories
- Predicted Extraction Profiles
The Bureau has developed a process using ion exchange to extract cobalt, a strategic and critical metal, from domestic copper leach solutions. These solutions are produced by dump or heap leaching of low-grade ores with dilute sulfuric acid and contain significant amounts of readily accessible cobalt. Although the cobalt concentrations in these streams are only 15 to 30 ppm, potential annual recoveries exceed 2 million lb. Current domestic consumption of cobalt is 13 million lb annually, 95 pct of which is imported from sources subject to supply disruption
The Bureau’s process uses ion exchange to extract the cobalt from the leach solution, followed by solvent extraction to purify and concentrate the cobalt. Metallic cobalt is produced by electrowinning. Economic considerations dictated that ion-exchange resin inventories in the Bureau’s process be minimized. Thus, the ion-exchange investigation was directed toward the use of a continuous, fluidized-bed, ion-exchange column. The Bureau-developed MCIX column was chosen for the cobalt recovery studies since previous work using this column to extract uranium from low-grade solutions had demonstrated its utility in reducing resin inventories when compared to fixed- bed systems. Ion-exchange resin Dow 4195.02 was used during the cobalt recovery investigation.
In addition, a procedure to numerically model the MCIX column, based upon the results of simple bench-scale tests, was developed to optimize its operation.
Although modeling of fixed-bed ion-exchange systems has been the subject of intensive investigations, results from these studies are not generally applicable to fluidized-bed systems. Previous approaches to modeling fluldized systems included approximation of a continuous ion-exchange column as a series of agitated resin slurries, but this approach required pilot plant data prior to complete model definition. Other modeling approaches required knowledge of terminal concentrations of the solution and resin phases or did not allow for possible changes in resin volume as metals were sorbed. More general modeling approaches have been published, but restrictive assumptions concerning reaction kinetics and mass- transfer rate expressions inhibited general application of these methods. Thus, the Bureau Investigated a general method to numerically model the MCIX column.
The objective of the Bureau’s numerical studies was to provide a dependable method of predicting MCIX column performance using minimal laboratory data. The Bureau-developed model used data from simple laboratory tests to establish equilibrium and kinetic parameters and resin-fluidization characteristics. Test results were then used in the numerical solution of a series of ordinary differential equations to predict MCIX column performance, and model predictions were compared to results from pilot-scale MCIX column experiments.
Cobalt Sorption Studies
Description of the Mcix Column
The Bureau-developed MCIX column consisted of a series of vertically arranged fluldized beds of Ion exchange resin (fig. 1). Stages, or sections, of the column were separated by orifice plates having an orifice area comprising 6 pct of the cross-sectional area of the column. Leach solution was introduced into the bottom of the column, and the upflow of solution fluldized the resin in each compartment. This fluidization was maintained except during brief intervals when resin was withdrawn from the bottom of the column. During these withdrawal periods, solution flow was interrupted, resin and solution in each stage were transferred to the next lower stage, and fresh resin was added to the top stage of the column. At the completion of the resin discharge period, solution flow was restored, and resin within the column was again fluidized.
Resin, discharged from the column, was eluted with H2SO4 and NH4OH to produce metal-rich eluate solutions and a barren, base-form resin, which was recycled to the MCIX column.
Description of the Ion-Exchange Resin
The resin used in the cobalt sorption studies, Dow 4195.02, is classified as a chelating resin. The resin consists of copolymerized styrene and divinylbenzene with attached bispicolylamine functional groups. The resin was minus 20 plus 50 mesh as received in the acid form, and was screened to minus 20 plus 28 mesh for use in the sorption studies. The minus 20- plus 28-mesh size fraction amounted to 50 pct of the as-received resin. The volume change associated with changing from the acid or metallic forms to the base form of the resin was minus 30 pct for the minus 20- plus 28-mesh resin.
Description of the Solution
The solution used in the cobalt sorption investigation was an effluent from a domestic copper cementation plant. The solution pH was 3.1, and the approximate metals content of the solution was, in grams per liter, 0.03 Co, 0.03 Ni, 0.06 Cu, 2.0 Fe, 0.2 Zn, 4.5 Al, 7.2 Mg, and 0.4 Mn.
Determination of the Equilibrium- Loading Isotherm
Although sorption studies emphasized removal of cobalt from the cementation effluent, Dow 4195.02 also sorbed nickel, copper, iron, and zinc from this same solution. Single-component equilibrium isotherms for the above metals in acidic sulfate solutions have been reported, but of more interest in the modeling investigation was the loading

isotherm for Dow 4195.02 in equilibrium with cobalt in the multicomponent domestic copper leach solution.
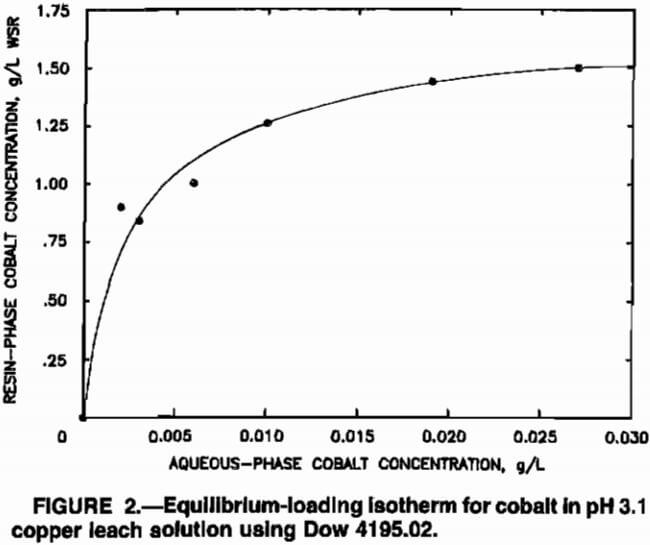
The equilibrium-loading isotherm for cobalt was determined by contacting cementation plant effluent with barren, base-form resin at aqueous-to-resin (A:R) volume ratios ranging from 1:1 to 300:1, at a constant pH of 3.1, in a stirred vessel at room temperature for 24 h. Preliminary research had indicated that 24 h was sufficient time for the resin and solution to reach equilibrium. Resin loadings were determined from a material balance using differences between fresh and spent solution assays. Equilibrium isotherms varied somewhat depending upon the exact composition of a particular sample of solution, but a typical equilibrium isotherm for cobalt is depicted in figure 2. The relative affinity of Dow 4195.02 for a number of the metallic cations in the copper leach solution has been reported as Cu²+ > Ni²+ > Fe³+ > Zn²+ > Co²+ > Fe²+. The resin had no significant affinity for other cations, such as aluminum, magnesium, and manganese in the leach solution. The difference in affinity of the resin for various cations in the leach solution suggested that sorbed cobalt ions could be crowded from the resin by ions for which the resin had a higher affinity. Crowding effects were not quantified in the modeling procedures since equilibrium isotherms were generated using actual cementation plant effluent; thus, the equilibrium isotherm depicted in figure 2 implicitly accounts for crowding.
Although fresh cementation effluent solution contained iron, primarily in the ferrous state, oxidation to the ferric state was rapid, and many of the solutions used in the investigation contained primarily ferric iron. The effects of iron oxidation were also accounted for implicity since both fresh and aged solutions were used in generating the equilibrium isotherms.
Cobalt Sorption Kinetics
Since the time required for the solution to pass through the MCIX column was
only 7.5 to 28 min, equilibrium between resin and solution was not achieved between resin discharges in the MCIX column. Consequently, loading kinetics had a significant effect on extraction efficiency. Studies were conducted to determine the rate at which cobalt was extracted from the spent copper leach solution by Dow 4195.02.
Cobalt sorption rates for the resin-cementation effluent system were determined in simple batch tests. Although sorption rates could be determined by a number of analytical procedures, a technique using a radiotracer was implemented since the very small sample sizes, typically 1 to 5 mL, required for analysis did not alter A:R ratios significantly during the tests. A trace amount of 60Co, 0.002 x 10 -6 Ci, dissolved in 0,1 H HCl, was added to 3 L of pH 3.1 cementation plant effluent. This solution was contacted with barren, base-form resin at A:R ratios between 30 and 60. These ratios spanned the practical operating range of A:R ratios for the MCIX column. Sufficient agitation was provided to ensure complete resin fluidization. Aqueous-phase cobalt concentration was determined by the rate at which gamma radiation was emitted by samples of solutions taken at various times during the batch experiments. Gamma radiation emission was monitored using an NaI scintillation detector with background correction. Emission rates were low, and
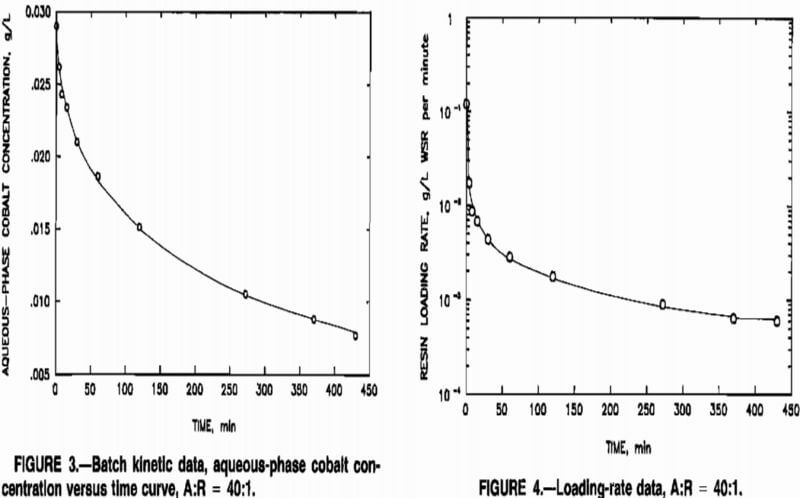
anticoincidence correction was not necessary. Cobalt concentration versus time was plotted for each A:R ratio, and sorption rates were determined by graphical determination of the slopes of the curves. The rates of sorption, in grams per liter of wet-settled resin (WSR) per minute, were estimated as the negative of the slopes of the curves at given times, multiplied by the A:R ratios. Data obtained at an A:R ratio of 40:1 are depicted in figures 3 and 4.
Initial cobalt sorption was rapid, and the concentration of cobalt in solution declined throughout the duration of the tests. The sorption rate changed only slightly after the first 2 h of the tests. The results depicted in figures 3 and 4 were typical of those obtained at other A:R ratios.
Resin-Fluidization Studies
Fluidization characteristics of Dow 4195.02 were determined by adding a mea-sured amount of resin to a 3-ft-high by 2-in-ID glass tube and fluidizing the resin with an upflow of solution at vari-ous liquid flow rates. Solution was introduced into the bottom of the tube through an orifice plate similar to those used between MCIX stages. The expansion of the resin bed was determined as a function of the superficial liquid flow rate by comparison of the height of the fluidized bed to the height of the WSR bed prior to fluidization.
This experimental procedure allowed investigation of the effects of changes in resin density due to loading on the fluidization characteristics of the resin. Water was used to fluidize the barren resin in laboratory tests since its viscosity was not significantly different from that of the leach solution, and the base-form resin would have sorbed metals from the leach solution. Both water and leach solutions were used to fluidize the loaded resin; no significant differences in fluidization characteristics were noted.
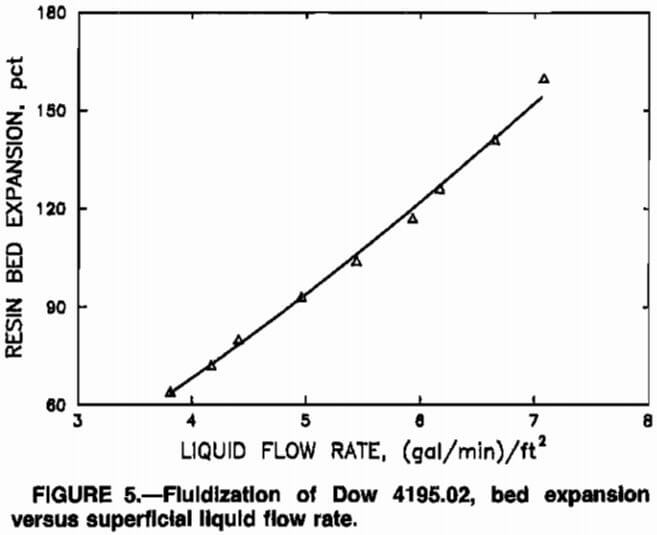
Data from the fluidization experiment, using loaded resin and leach solution, are depicted in figure 5. The curve in figure 5, percent expansion – 9.331(Q)1.434, where Q is the liquid flow rate in gallons per minute per square foot, was established by applying a least-squares procedure. The equation for the curve was used to determine the MCIX column resin inventory in the modeling studies.
MCIX Column Modeling Studies
The objectives of MCIX modeling research were (1) to develop a numerical model that could correctly predict cobalt extraction and resin inventory at a specified set of MCIX column operating conditions, and (2) to determine the requisite laboratory data for making such a prediction.
Mathematical Basis For The Model
General Kinetic Model
The rate at which Co²+ ions were extracted from solution was dependent on the concentration of cobalt in solution, the concentration of cobalt on the resin, and the equilibrium capacity of the resin in contact with the cobalt-bearing solution. Thus, the extraction rate was expressed by an ordinary differential equation of the form
(dY/dt) = kl·Caα·(l – Y/Y)β………………………………………………………………….(1)
where Y was the concentration of cobalt on the resin in grams per liter WSR, kl, α, and β were experimentally determined constants, and Y was the concentration of cobalt on the resin that would be in equilibrium with pH 3.1 cementation-plant effluent containing Ca grams per liter of cobalt.
The equilibrium-resin concentration, Y, was expressed as a function of solution composition according to the relationship
Y = A(Ca) / (B(Ca) + 1)……………………………………………………………………………(2)
where A and B were determined empirically using equilibrium data and curve-fitting procedures. The values for A and B, which described the isotherm depicted in figure 2, were 550 and 325, respectively, but values of A and B that best described the equilibrium resin loading of cobalt differed for various samples of cementation plant effluent owing to variations in solution composition.
The values of k1, α, and β in equation 1 were obtained from previously described batch loading-rate tests. Loading rates were determined from plots of the experimental data from the batch experiments, and equation 1 was approximated by the linearized form
ln(-dCa/dt) = ln(k1) + α·ln(Ca) + β·ln(l – Y/Y)………………………………………………………(3)
A multiple linear regression procedure yielded approximate values for k1, α, and β. Correlation coefficients from the regressions were typically 0.8. Attempts to improve the accuracy of the values of k1, α, and β using nonlinear least-squares procedures were unsuccessful.
Numerical Loading-Rate Equations
A cobalt material balance on the resin phase between discharges was approximated using an Euler method to solve equation 1 for each stage of the MCIX column. The numerical expression used in the model was of the form
![]()
where the subscript i denotes the MCIX stage number, the superscript t denotes time, and Δt is the time increment used in approximating the solution to equation 1. The solution to the set of equations represented by equation 4 required initial conditions for both the resin and solution-phase cobalt concentrations in each section of the column. For simplicity, the following initial conditions were chosen:
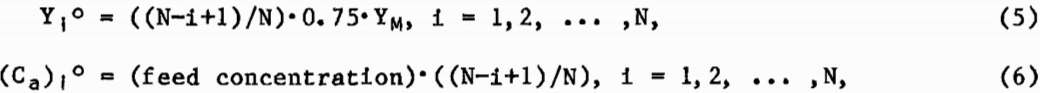
where N was the total number of MCIX stages and YM was the maximum loading of cobalt on the resin as determined from the equilibrium Isotherm, using the initial leach solution concentration as the abscissa. The modeling of the column was performed such that any reasonable set of initial conditions for the resin and solution concentrations would be adequate, but the above set of initial conditions accelerated convergence of the calculations.
Since local concentration gradients and mixing transients in a single MCIX stage are highly complex, average resin and aqueous-phase concentrations were assumed to prevail, and equations 1, 3, and 4 were applied to each MCIX stage with Y1, (Ca)1, and Y1 taken as average quantities for each stage during the current time interval.
Determination of Resin Inventory
The resin inventory in the column was determined by correlating laboratory measurements of the resin bed expansion at various superficial liquid velocities. The resin inventory was then determined from the following expression:
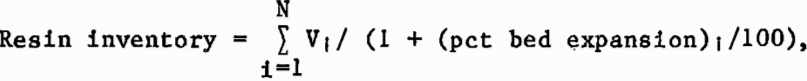
where percent bed expansion = a·Qb·Y1c, N was the number of MCIX stages, V1 was the volume of a single MCIX stage, Q was the liquid flow rate per unit of cross-sectional column area, and a, b, and c were empirical constants estimated by application of a least-squares procedure to the data from the resin-fluidization tests, depicted in figure 5.
Determination of Loading Cycle Length
The amount of time between resin discharges in the MCIX column was determined based on the amount of loaded resin discharged, the liquid flow rate, and the A:R ratio. One hundred percent of the resin and solution in each stage were assumed to transfer to the next lower stage during a discharge, although the model allowed for less than a full compartment to be discharged during a simulation. The cycle length was determined to be the volume of WSR in the bottom compartment, multiplied by the fraction of resin and solution in each stage to be transferred during a discharge, divided by the quotient of the liquid feed rate and A:R ratio.
Since the volume of displaced solution due to expansion of the loaded resin was insignificant compared to the amount of solution passing through the column during the loading cycle, the displaced solution was not considered in determining the loading cycle length.
Modeling Algorithm
The step-by-step procedure used in the modeling calculations may be summarized as follows:
- Specify the number of MCIX stages, column dimensions, A:R ratio, liquid feed rate and feed concentration, fraction of resin and solution in each stage to be transferred during a resin dis-charge, and number of discharge cycles to be simulated. The number of cycles required for the model to reach steady state was approximately four times the number of MCIX stages.
- Set initial resin and solution compositions.
- Estimate the stagewise and total resin inventories.
- Estimate the length of the loading cycle.
- Calculate the equilibrium resin-phase concentration and sorption rates for each stage during the current time increment.
- Calculate the amount of metal sorbed during the current time increment and the new resin compositions for each stage.
- Calculate new solution compositions basfed upon the amount of metal sorbed onto the resin and the flow of solution through each stage during the current time increment.
- Check to see if a loading cycle was completed. If so, check, to see if the specified number of discharge cycles have been completed. If so, then the simulation is complete. Calculate the desired instantaneous and total metal extractions. Print extractions and resin and solution concentration profiles; then terminate program execution. If the specified number of cycles were not complete, transfer the solution and resin in each stage to the next lower stage, add barren resin and spent solution to the top compartment, increment the current time, and proceed to step 5.
The modeling algorithms is depicted as a simplified flowchart in figure 6. Computer code was written in FORTRAN to implement the algorithm on a microcomputer, and model results were compared to data obtained from a pilot-scale MCIX column. A copy of the FORTRAN source code may be obtained from the authors.
Dynamic Behavior Of The Mcix Column
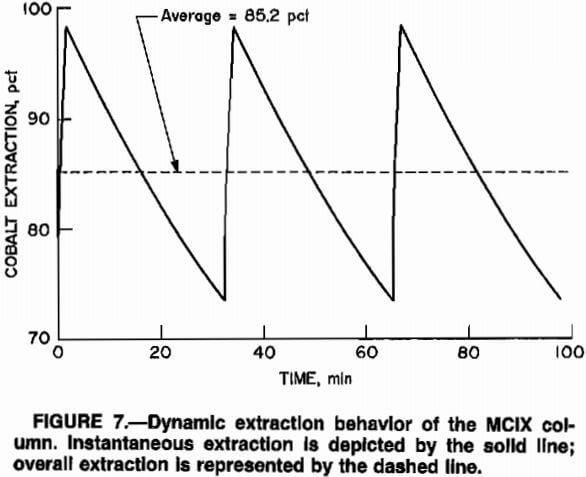
The percentage of the cobalt in the feed solution extracted by the resin in the column varied throughout the length of a loading cycle owing to the cyclic mode of operation of the MCIX column. Resin was transferred periodically, while solution moved continuously. Thus, the resin in a particular MCIX stage had less metal on it at the beginning of a cycle than at the middle or end of the cycle. Sorption rates and metal extractions were higher early in the cycle, and as the cycle progressed, sorbed metal reduced the difference between the equilibrium resin-phase metal concentration, Y, and the average concentration of metal on the resin, Y, in a particular stage. Since the difference between the resin loading and equilibrium loading constituted the driving force for mass transfer, the extraction rates decreased as the cycle progressed. This decrease in the mass-transfer driving force was only slightly compensated for by the increased average solution-phase concentration that resulted from the lower extraction rates, and the trend during the loading cycle was one of decreased extraction.
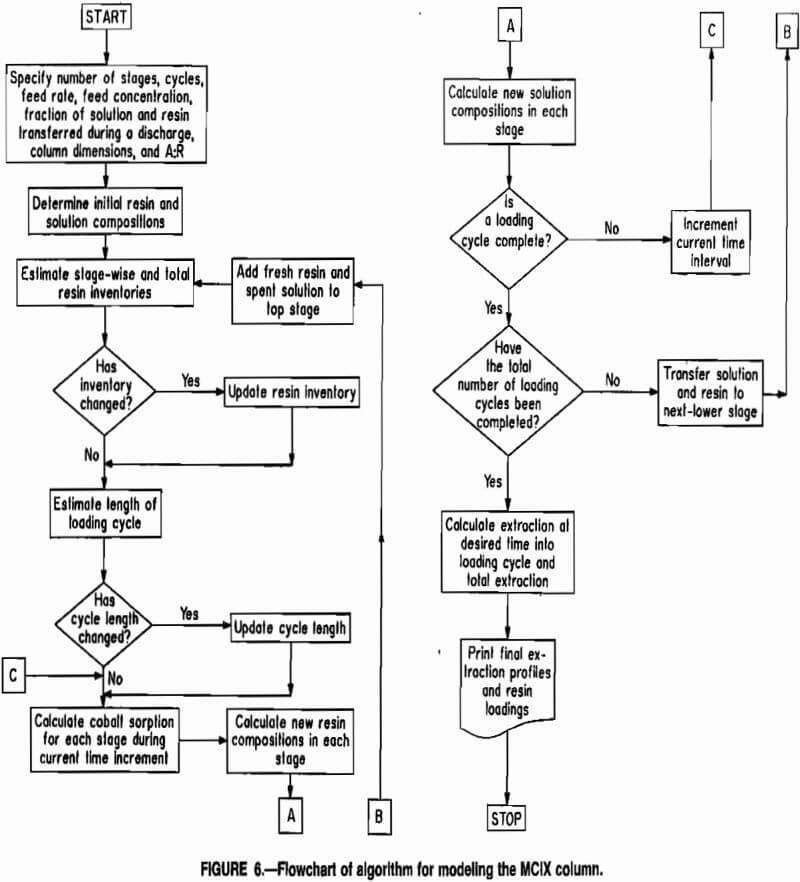
Figure 7 is a plot of the predicted, transient performance of a 15-compartment MCIX column, operated at an A:R ratio of 40:1 and a solution flow rate of 5.5 (gal/min)/ft².
Figure 7 suggests that shorter cycle times would result in greater total recoveries since the valleys in the instantaneous recovery curve would be more shallow. While this is true, the net result of faster cycle times would be incomplete utilization of the ion-exchange resin, i.e., the A:R ratio would be decreased owing to the increased resin flow rate, and resin discharged from the column would be only partly loaded. While cobalt recoveries might be greater at lower A:R ratios, resin inventories would be unreasonably large, and resin costs would be correspondingly high.
Comparison of Model Predictions To Mcix Column Data
Predicted Optimum Operating Conditions
Optimum operating conditions and cycle times for a MCIX column must be determined by a balance between product values and capital and operating costs. Owing to the high cost of the ion-exchange resin used in the Bureau’s cobalt recovery studies, the Bureau’s 2-in-ID MCIX column was operated to obtain maximum cobalt recovery per unit of ion-exchange resin. Maximum cobalt extraction per unit of resin was achieved in a column consisting of ten 1-ft compartments, at an A:R ratio of 40:1, using a solution feed rate of 5 (gal/min)/ft² and a 41-min cycle time. Modeling studies predicted maximum cobalt recovery per unit of resin would occur at the same set of operating conditions.
Predicted Cobalt Extractions and Resin Inventories
Owing to the dynamic behavior of the MCIX column, actual and predicted metal extractions must be compared at specified times during a loading cycle. During most of the cobalt sorption studies, MCIX-column extraction profiles were taken 20 min into the loading cycle. Thus, model predictions of extractions were calculated 20 min into the loading cycle for comparison. For conditions resulting in a cycle time of less than 20 min, comparisons were made at the end of the loading cycle. Actual and predicted extractions for various MCIX column experiments are summarized in table 1.
The MCIX column stages used in the 10- and 15-compartment experiments were 1 ft
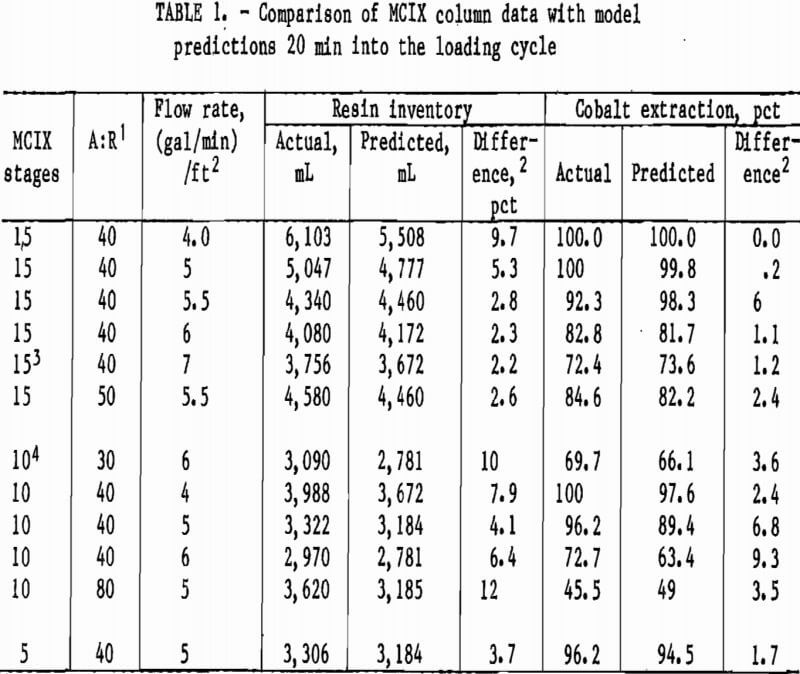
high by 2-in-ID, while the stages used in the 5-compartment experiment were 2 ft high by 2-in ID. Data and predictions agreed well for both the resin inventory and cobalt extractions. The average difference between predicted and actual cobalt extractions was 3.2 pct, while the maximum difference was 9.3 pct. The actual and predicted resin inventories differed by an average of 5.8 pct, and the maximum difference was 12.0 pct.
Predicted Extraction Profiles
Stagewise extraction profiles, indicating model predictions and actual MCIX column data, are depicted for various MCIX column experiments in figures 8 to 12. Although extraction profiles might be of less significance than predictions of quantities that influenced process economics, i.e., total extraction and resin inventory, the profiles aid in
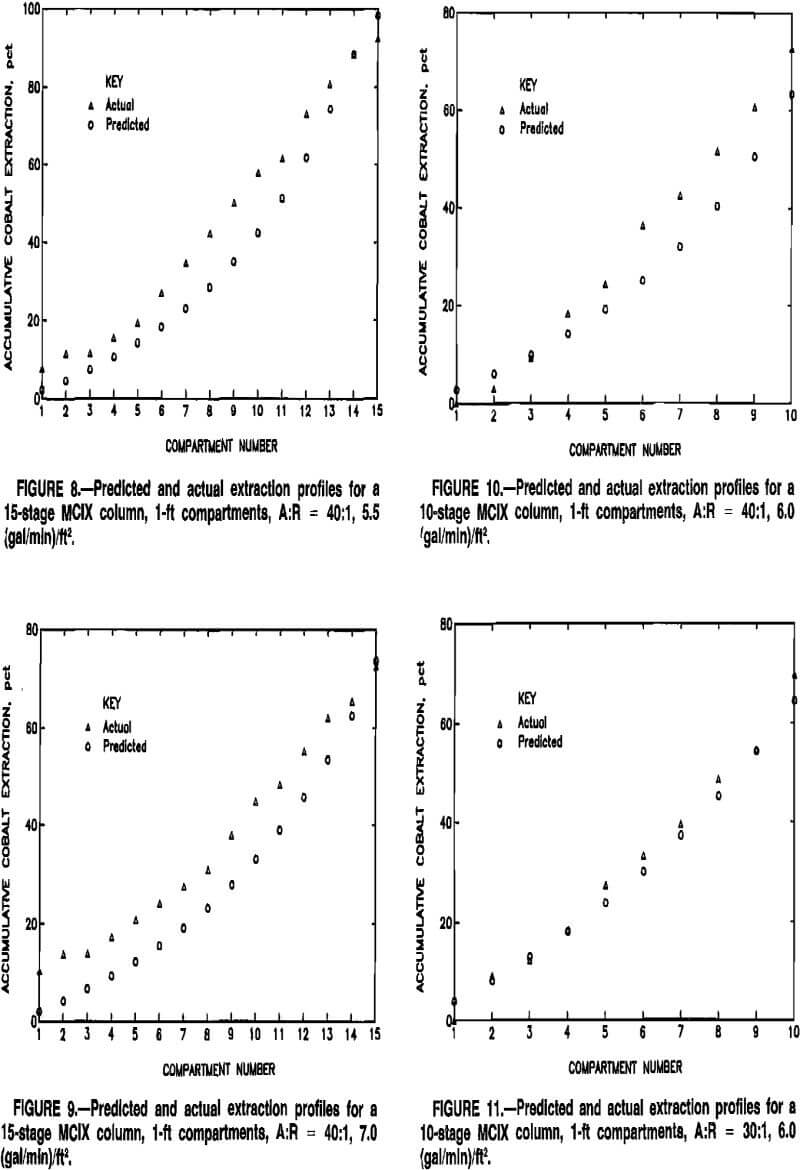
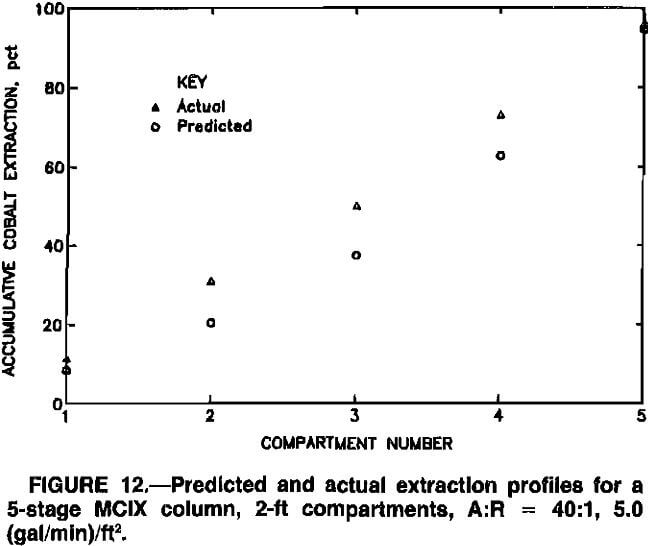
evaluating the ability of the model to reflect actual conditions within the MCIX column. Compartment numbers in figures 8 to 12 correspond to the sequence of compartments in the MCIX columns, with 1 being the bottom compartment. Model predictions were usually slightly lower than the actual extraction profiles in the lower and middle sections of the column, possibly because only a first-order numerical method, i.e., Euler’s method, was used in approximating the solution to the loading-rate equations. A higher order solution method, e.g., a Runge-Kutta or a predictor-corrector method, may result in more accurate extraction profiles. In all cases, however, model predictions were within a few percent of actual cobalt extractions.
Summary
The Bureau-developed numerical model of the MCIX column accurately predicted MCIX column performance on the basis of simple laboratory test results. Eight parameters, determined in simple laboratory tests, were necessary for complete model definition. Equilibrium resin and aqueous-phase cobalt concentrations were determined by contacting barren resin with cementation effluent at A:R ratios from 1:1 to 300:1. The resin-phase concentration, Y, was plotted against the aqueous-phase concentration, Ca, and constants A and B were determined to express the equilibrium-loading isotherm as
Y = A(Ca)/(B(Ca) + 1).
Cobalt extraction rates were assessed, and constants k1, α, and β were determined to approximate the extraction rate as
(dY/dt) = k1·Caα·(l-y/Y)β.
Finally, resin fluidization tests were conducted, and the resin-bed expansion was correlated by
percent bed expansion = a·Qb·Yc.
These eight parameters, A, B, k1, α, β, a, b, and c, were used in a numerical model to predict metal extractions and resin inventories in the MCIX column under a number of different operating conditions.
Results compared very well to data from 12 pilot-scale MCIX column experiments. The average difference between predicted and actual cobalt extractions was 3.2 pct; the maximum difference was 9.3 pct. The actual and predicted resin inventories differed by an average of 5. 8 pct, and the maximum difference was 12.0 pct.
