A number of compressive tests were conducted on iron ore pellets obtained from the Samarco pelletizing plant located at Ponta Ubu, Brazil. These pellets are formed by disk pelletizing of a mixture consisting of hematite iron ore, (particle size less than 50 µm) water, and lime; they are hardened in a traveling-grate furnace and the nominal diameter varies between 9 and 16 mm. The pellets were tested at ambient temperature in a Tinius-Olsen and in a Riehle universal testing machine. A cross-head velocity lower than the one recommended by I.S.O. (1974) was chosen in order to allow for a greater ability to control the test parameters. The fracture occurred most often along a vertical plane; the sphere was divided into two or more parts by the fracturing process. Figure 4 shows a top view of a fractured pellet, which was divided into two and three parts. A closer observation of the fracture surface with a scanning-electron microscope revealed features that definitely establish, the fracture process as a tensile cleavage-type (Fig, 5) . The fracture is transgranular: it goes through the original hematite particles, that are smaller than 50 µm. These invididual particles can be seen very clearly. The fracture surface in the region between the particles is not as smooth as inside the particles. The binding material used for the green pellets, hydraced lime and silica, actually melt during the pellet-hardening stage and forms a bond between the hematite particles. Figure 6 shows elemental scans of a region resembling the interface between three fractured particles. The presence of silicon and calcium is very clear along the interfaces, which accordingly are denuded of iron. This shows that the fracture is indeed transgranular and that the interface region has the same or greater tensile strength than the hematite particles.
The region immediately adjoining the platen-pellet contact has a completely different morphology. On visual observation, it exhibited a reddish coloration, in contrast with the metallic luster exhibited by the cleavage region, which consists of about 98 pct of the fracture surface. Observation by scanning electron microscopy confirms the completely different morphology indicative of different operating fracture mechanism. Figure 7(a) shows a flat portion corresponding to the contact surface of the pellet and a more irregular region adjoining it. This more irregular region is magnified in Figure 7(b). In contrast with Figure 5(b) the particles are much smaller and more irregular. Their size is around 5 µm; hence, the original hematite particles are crushed. This feature is clearly indicative of shear failure. The extremely high compressive stresses set up at the contact region generate, at 45°, shear stresses that fracture the hematite particles. The existence of such a shear failure region has been recognized by Jaeger and Cook (1979) and Kapur and Fuerstenau (1967).
Jaeger and Cook (1979) do not attribute any importance to it in establishing the complete fracture. Hence, one can conclude that the fracture of the pellets is indeed caused by tensile stresses, that are maximum at the center.
Figure 8(a) shows a first attempt at correlating the pellet dimension with fracture strength in accord with Equation 16 derived in the preceding section. The pellet cross-sectional area was obtained by computing it from its weight, assuming a sphere. The density was obtained by measuring the diameter of pellets that were hand-ground in order to render them more spherical; it was found to be 3.83 g/cm³. The first observation that can be made is that the scatter in the data is very large. There are several possible causes for this: pellet irregularity, existence of internal voids, intrinsic variations in strength, size. In spite of the wide scatter, a least-squares fit shows clearly a tendency towards greater strength with greater cross-sectional area. The line intersects the load axis at -700N. Kapur and Fuerstenau (1967), on the other hand, plotted the pellet strength (limestone pellets) versus the mass, and fitted the relationship into a straight line. In order to (a) extend the range of pellet size beyond the one available and (b) to verify whether surface imperfections might be responsible for the variation in strength, pellets were polished in a rotating disk with sandpaper prior to testing. Figure 8(b) shows the results, and the P versus πd² correlation is much clearer, especially at small sizes. One can see that polishing the surface does not have a noticeable effect on the variation of strength; one has to conclude that there is an intrinsic strength variation between individual pellets. The intercept of the least-squares-fit have is 0.265, kN, and the standard deviation of this intercept is 0.340 kN; hence, one can safely say that the line passes through the origin. The slope is 2,262 kN/cm².
In an attempt to investigate the effects of internal voids on the strength of pellets, diametral cuts were made on two pellets with a diamond blade saw (Isomet). The composite photograph obtained by scanning electron microscopy operating at the minimum magnification is shown in Figure 9. The significant density of voids is clearly seen; they vary in size from zero to -0.3 mm. The large porosity exhibited by the pellets is due to the fact that they are not compacted or densified and water is trapped between the particles in the green pellets, being later expelled during the sintering process. At a larger magnification (Figure 10) these voids exhibit rounded features inside due to the viscous flow of the materials during sintering. The density of the voids was measured at a magnification of 22 x using the Spektor’s method described by de Hoff and Rhines (1968). The voids are assumed to be spherical and the chord length is measured by the intercept method. The total length of lines on which measurements were made was 900 mm and a total of 1300 voids was counted. Figure 11 shows the densities of voids in the different size groups. The void sizes below -0.04 mm cannot be seen at the magnification in which the measurements were made; hence, they are not included in the plot of Figure 11. The presence of these voids can have a profound effect on the mechanical strength of the pellets. In the field of fracture mechanics the effect on the mechanical strength of the pellets. In the field of fracture mechanics the effect of flaws on the mechanical properties of materials is studied; the effect of a void is to generate a stress concentration at the void tip. The effect of a flaw on the stress is usually described (e.g., Hertzberg (1976) and Knott (1973)) as:
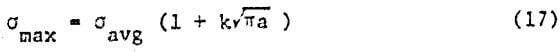
σavg is the average stress, a, the length of the flaw, and k is a constant. The expression assumes a flaw with sharp edges. Although the voids were considered spherical in the previous calculations, at the microscope level they present irregularities (like gaps between individual hematite particles) that fulfill the requirement to be considered as a flaw. Hence, the tensile stress experienced by the center of the pellet (Equation 16) has to be corrected for the existence of flaws:
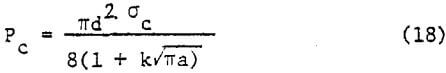
For instance, a small pellet chat does not have a void in the center might be stronger than a larger pellet with a flaw.

