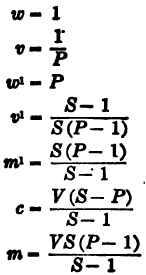To find weight of a given volume of sand or similar material. In cases where it is not convenient to weigh the entire charge direct, the wet and dry weight of a charge is often ascertained by allowing a vessel of known capacity, say a large cubical or cylindrical box, to be filled at the same time and in the same manner as the tank or other container in which the material is to be treated. When the charge is completed, the surface is levelled off without pressing down and the box and contents weighed on a platform scale or suitable balance. The entire charge is also levelled and its volume computed from the known dimensions of the containing vessel. In the case of a cylindrical tank,

V (volume) = π r²h.
where r = radius of tank.
h = average depth charged with material.
π = 3.14159 ( = 22/7 approximately).

In the case of a conical vessel,

V = πr²h/3
where r = radius of circle forming upper surface of mass of material filling cone.
h = depth from surface to apex of cone.
π = 3.14159 ( = 22/7 approximately).

After weighing the sample, a sufficient quantity, say 1 or 2 kg. (4 or 5 lb.) is weighed separately, spread out in a thin layer on a metal tray, and dried at a moderate heat. After drying the tray and contents are re-weighed and the percentage of moisture calculated.

The wet weight of the charge is then easily calculated as follows:

Let W = wet weight of charge.
v = volume of sample,
ω – wet weight of sample.
h = depth charged in tank (average),
r = radius of tank.
Then v: πr²h: : ω: W.
or, W = πr²hω/v

The value of h is deduced from the average of a number of measurements taken at different parts of the surface to determine the depth left empty between the top of the tank and the charge.

The dry weight of the charge, D, is calculated from p, the percentage of moisture, as follows:

D: W:: 100 – p: 100
or D = (100-p/100)W

(b) To find the weight of a given volume of wet pulp (e.g., a charge of slime).
In cases where the material is of such a nature that all the interstices between the particles are filled with liquid, as in a charge of slime mixed with water or cyanide solution, the total dry weight may be calculated from the following data:

V = total volume of charge.
P = density (specific gravity) of pulp.
S = density (specific gravity) of the dry material.

The total volume (V) is determined as already described, from the known dimensions of the containing vessels. We may define the density or specific gravity of a substance as the ratio between its weight and the weight of an equal volume of water at a temperature of 4° C. At that temperature the weight of 1 cc. of water is 1 gram; hence the density of any liquid or solid is the weight in grams of a measured quantity, divided by the number of cubic centimeters which it occupies.

The density of the pulp is determined by filling a vessel of exactly known volume, for instance a liter flask, with an average sample of the pulp and weighing its contents. The volume of the containing vessel need not be known, if the weight of water filling it to the mark be ascertained. In this case a correction is required for the expansion of water if the determination be made at any other temperature than 4° C., though this is negligible for most practical purposes.

The density of the dry substance of which the pulp is formed is generally found by weighing a certain amount of a carefully dried average sample, placing it in a vessel of known capacity and filling up to the mark with distilled water. The weight of the vessel filled with water alone is also determined. Before weighing the vessel containing the material and water, it is necessary in some cases to immerse it for one or two hours in boiling water up to the neck, leaving the stopper out, to allow the expulsion of any air contained in the dry powder. It is then cooled and weighed. The density of the dry material may then be calculated as follows:

Let m = weight of dry substance taken.
a = weight of water filling vessel to mark when no substance is added.
b = weight of substance together with amount of water required to fill vessel to mark after substance has been added.
c = weight of residual water.
d = weight of water displaced by dry material.
8 = density of dry material.
Then b = m + c
d = a — c
s= m/d = m/a-c = m/m + a – b
Or let W1 = weight of vessel when filled with water to mark.
W2 = weight of vessel with dry material, filled up with water to mark.
Wo = weight of empty vessel
Then a = W1 — Wo
b = W2 — Wo
and s = m/m + W1 — W2

The weight of dry material in the total charge may then be calculated from the known values of P and S.

This formula is subject to the same correction for expansion of water which is involved in calculating the value of P.

(c) Useful data deducible from the above formulae.
(1) Percentage of dry material in a charge of pulp.

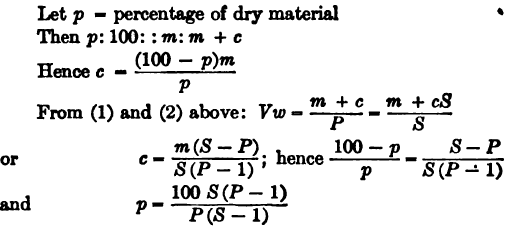
(2) Percentage of solution in a charge of pulp.

q = percentage of solution
q = 100 – p = 100(S – P)/P(S – 1)

(3) Ratio of solution to dry material (R).

R = q/p = S – P/S(P – 1)

(4) Volume of unit weight of pulp (v).

v = V/m + c = 1/wP

(5) Weight of unit volume of pulp (w1).

w¹ = m + c/V = wP

(6) Weight of dry material per unit volume of pulp (m1).

m¹ = m/V = wS(P – 1)/S – 1

(7) Volume of pulp containing unit weight of dry material (v1).

v¹ = V/m = S – 1/wS(P – 1)

(8) Total weight of solution in charge of pulp (c).

c = Vw (S – P)/S – 1

(d) Application of the above formulae to particular cases.

(1) Weights in pounds avoir. Volumes in cubic feet. — 1 cu. ft. of water = 62.5 lb.

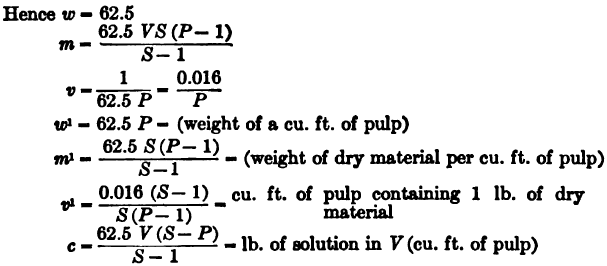
(2) Weights in tons of 2000 lb. Volumes in cubic feet. — 1 ton of water = 32 cu. ft.

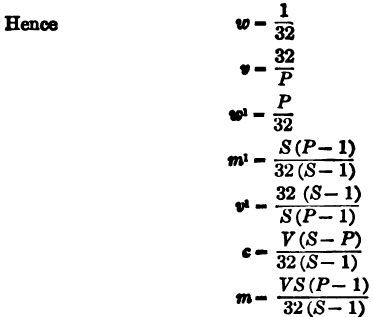
(3) Weights in metric tons of 1000 kilograms. Volumes in cubic meters. — 1 ton of water = cu. meter.