Table of Contents
In the previous chapter the influence of the various physical quantities defining the mill and mill charge has been studied in connection with the performance of a mill as a device for the creation of new surface in the powder. For some purposes, however, it is also desirable that the product should have a preferred form of size distribution curve. For example, in mineral dressing it is usually necessary that the material below about 200 mesh should be a minimum. To some extent such modifications in the size distribution characteristics can be brought about by changes of the mill dimensions. It must be emphasized, however, that such changes are of limited scope but, even so, are often worth-while.
Effect of Ball Diameter, or Rod Diameter Variation
The first relationship to be considered is the effect of the variation of the ball diameter, or rod diameter, upon the size distribution obtained. In Fig. 6.1 are shown typical size frequency curves obtained by ball milling; these curves being deduced from the data of Coghill and Devaney.
As would be expected, the grinding of a coarse feed with small balls does not give rise to the effective grinding of the coarse particles in the feed but does produce a considerable amount of fine product. For the largest ball sizes, however, rapid grinding of the coarse fraction is attained. Turning attention to the finer feed, however, it will be observed that the largest ball size gives a coarser product than does the next size smaller balls. Thus it appears that

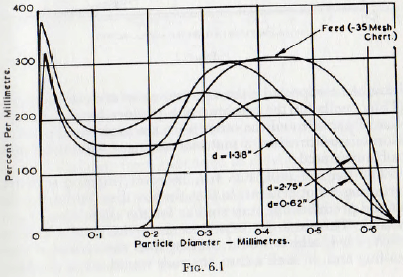
the coarser fractions may be ground, without the production of excessive fine material, by the use of balls of large diameter; however, the particle size must not be excessive or this benefit is lost.
From these rather limited data it would appear that the best selective grinding is obtained when the ball diameter is about 100-150 times that of the particle to be crushed. This figure is very roughly in accordance with that which would be deduced from Fig. 5.12, but close agreement
cannot be expected since the two cases are not identical. Thus one is for the crushing of a powder having a single size of particle and the other is for the most rapid production of surface when a material having a wide size-range is comminuted.
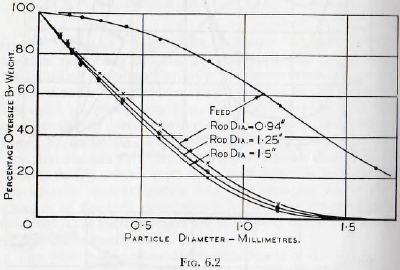
For the rod mill, Fig. 6.2, however, marked selective grinding is not evident; in fact the size distribution curves of the products are very similar for the three sizes of rod tested. This is to be expected since the results are for N/Nc = 0.4, which would suggest that the charge is cascading and, in such a case, the rods would act as crushing rolls loaded to give a constant force. Thus, the larger particles would be the first to be broken, whatever the size of the rods. It is possible that the grinding characteristics would be different when the charge is cataracting, but evidence on this point is not available.
Grinding Media Density Variations
Examination of Fig. 6.3 shows that variations in the density of the grinding media does not have great effect in selective grinding; although the use of the more dense mils does very slightly increase the preferential grinding of the coarser fractions in the feed. Since, however, it is not
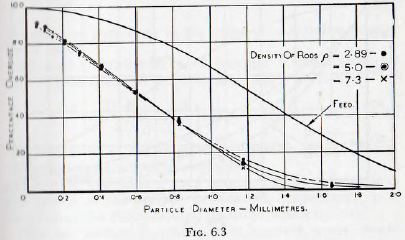
practicable to select grinding bodies made from materials of a wide range of densities, interest in the effects of this variable are theoretical rather than practical. (It should be noted that these tests have been run for times such that equal work has been expended in driving the mill. Thus, it follows that the expenditure of equal amounts of work produce practically identical products from the same feed, regardless of the density of the grinding media.) When the ball charge is fixed, variation of the quantity of ore in the mill brings about no significant selective grinding between the different sizes of material in the feed.
Mill Efficiency & Mill Filling
The relationship between mill efficiency and mill filling will now be studied.
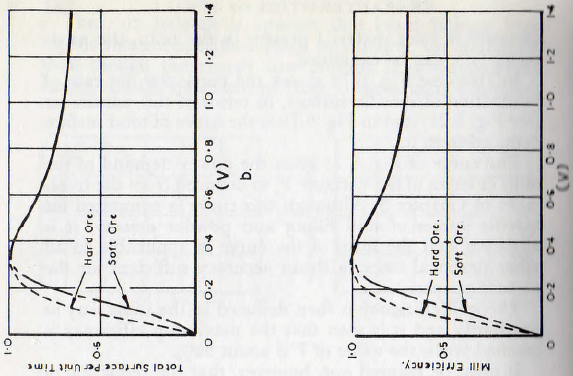
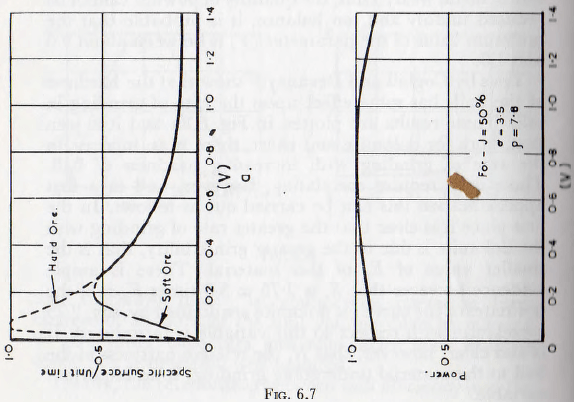
In Fig. 6.6a is shown the curve relating the rate of production of specific surface to the mill filling (see Fig. 5.19)) and in Fig. 6.6b is the curve of total surface production, per unit time, deduced from it. The curve Fig. 6.6c is that of power input to the mill and is, in fact, the curve of Fig. 3.5.
The mill efficiency is then deduced by the division of the ordinate of curve Fig. 6.6b by that of Fig. 6.6c and the curve so obtained is plotted in Fig. 6.6d. From this graph it is seen that the mill efficiency is sensibly constant for fillings of up to about 50% and that for greater fillings the efficiency increases rapidly.Thus, it would appear that, for the greatest efficiency, a large filling, say 75%, should be used. This is only partially true, however, for with such a filling the rate of production of specific surface is reduced and so to obtain a product of given fineness the milling time must be increased. If the energy to cause comminution were all that is involved, this would be immaterial, but the energy lost in friction in gearing, bearings, etc., is almost independent of the charge in the mill and this loss is minimized by the reduction of the milling time to a minimum. Furthermore, the reduction of the milling time liberates the plant for other duties and so is economically desirable.
Thus, on balance it appears that lower fillings, with higher rates of specific surface production, are desirable, even though the energy consumption is proportionately larger, and the statement by Gow, Guggenheim, Campbell and Coghill that: “In commercial operation large charges of 55-60% of the mill volume have been found to give lower capacities and efficiencies than loads of 45-50%”, is probably well founded.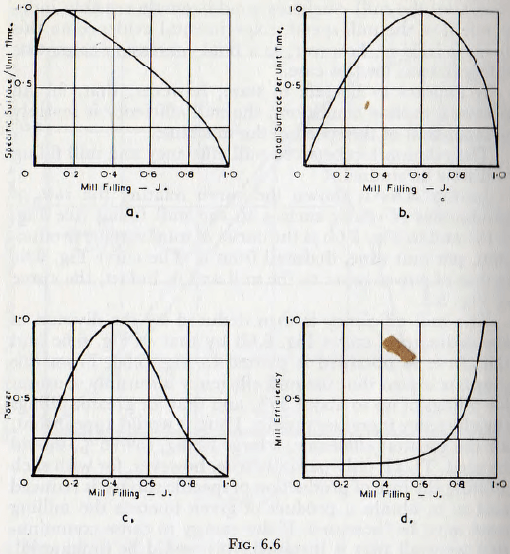
Finally, the relationship between mill efficiency and the quantity of solid material present in the pulp, the parameter (V), can be examined.
In this case Fig. 6.7a shows the curve for the rate of production of specific surface, in terms of this parameter (see Fig. 5.21) and in Fig. 6.7b is the curve of total surface deduced from it.
The curve of Fig. 6.7c gives the power demand of the mill, in terms of the variable V, so deduced from the treatment of Chapter 3. Although this curve is computed for specific values of mill filling and powder density, it is probable that the form of the curve is applicable to all other practical cases, with an accuracy sufficient for the present purpose.
The mill efficiency is then deduced in the same way as previously and it is seen that the maximum efficiency is reached when the value of V is about 30%.
It must be pointed out, however, that the reduction of the quantity of powder in the mill leads to an increased rate of metal wear. Thus, the quantity of powder cannot be reduced unduly and, on balance, it is probable that the optimum value of the parameter (V) is between about 0.6 and 1.0.
Effect of Balls Hardness on Rate of Grinding
Tests by Coghill and Devaney show that the hardness of the balls has some effect upon the rate of grinding in mill. These results are plotted in Fig. 6.8a and it is seen that, both for dolomite and chert, there is an increase in the rate of grinding with increasing hardness of ball. These data require correlating, however, and as a first approximation this can be carried out as follows. In the first place it is clear that the greater rate of grinding with the dolomite is due to the greater grindability, that is the smaller value of E, of this material. There is ample evidence however that Ec is 2.75 to 3.0 times Ed so if the ordinates of the curve for dolomite are divided by, say, 2.75 correlation with respect to this variable is introduced. It is also clear, however, that H, the relative hardness of the ball to the material undergoing grinding, is an important variable.
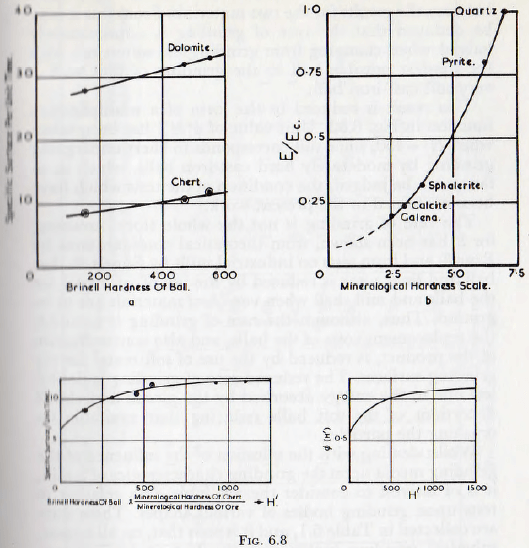
Now a curve by Fahrenwald, shown in Fig. 6.8b, relating grindability to mineralogical hardness, suggests that a reduction in the value of E from 1.0 to 1/2.75 corresponds to a reduction of mineralogical hardness from 1.0 to 0.5 and so the relative hardness of the ball to the dolomite is twice that of the ball to chert. Thus the abscissae values of the curve relating to dolomite must be multiplied by 2.0. When this is done the curve of Fig. 6.8c is obtained and it is seen that there is fair agreement between the results for the two materials. From this it may be deduced that the rate of grinding is approximately halved when changing from grinding the softest ore with the hardest possible ball to the grinding of flint with a very soft cast-iron ball.
This result is reduced to the form of a multiplicative function in Fig. 6.8d. Unit value of ∅(H’) has been taken when H’ = 450, since this corresponds to chert undergoing grinding by moderately hard cast-iron balls, which is, as far as can be judged, the condition of the tests which have been examined in the present work.
The rate of grinding is not the whole story, however, for it has been shown, from theoretical considerations by Rose and from tests on industrial mills by Engels, that ball and liner wear is reduced by the use of soft metal for the balls and mill shell when very hard materials are to be ground. Thus, although the rate of grinding is reduced, the replacement costs of the balls, and also contamination of the product, is reduced by the use of soft metal for the grinding surfaces. The reduced rate of grinding is doubtless due to the energy absorbed by the plastic and elastic distortions of the soft balls reducing that available for crushing the particles.
Whilst dealing with the question of the influence of the grinding media upon the grinding characteristics of a mill, it is of interest to consider the available data relating to tests upon grinding bodies of various shapes. These data are collected in Table 6.1, and it is seen that, on all counts, spherical grinding bodies give the highest performance figures. Thus, although it might be economical to use large lumps of ore, or “cylpebs” made from scrap drill-rods, when such are available at the plant, there appears to be no economic justification for the use of grinding bodies of shape other than spherical when the bodies have to be purchased at comparable prices.
The increase of power demand brought about by the use of bodies of non-spherical form would be expected;
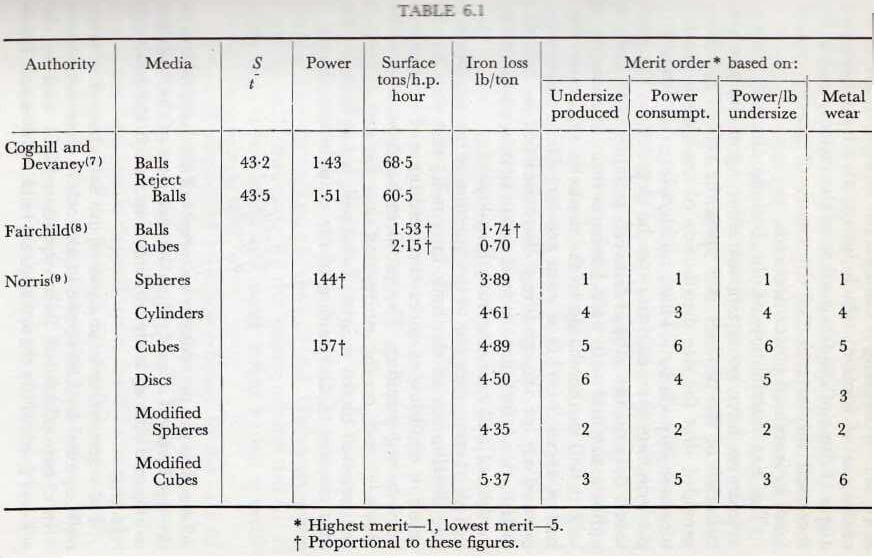
since the interlocking is tantamount to an increase in the coefficient of friction, which brings about an increased angle of slope of the free surface of the charge, and so an increased displacement of the centre of gravity, which leads to increased power demands.
Size Distribution of the Balls in the Mill Charge
The size distribution of the balls in the mill charge appears to have no significant effect upon the size distribution of the product, nor upon the rate of grinding, provided that the size distribution of the balls is not too unreasonably chosen. Thus, no significant difference in the grinding characteristics can be detected in the published data on the subject between grinding with balls of uniform size and with balls having a ratio of diameter of largest ball in the charge to the diameter of the smallest ball of about 2 to 1.0 or even greater. This comparative insensitivity of the grinding characteristics to ball-size distribution is fortunate since it means that any convenient method of ball rationing may be adopted.
This at once gives rise to the question of the equilibrium size distribution of the balls in a mill; this distribution being in equilibrium under the conditions of wear which hold during grinding. The problem has been studied by Davis, and, on the assumption that the rate of wear is proportional to the weight of the ball, it has been shown that the size of distribution of the equilibrium charge is given by
![]()
where W is the percentage by weight of the balls falling in the size interval da to db, dm is the diameter of the balls fed to the mill and d0 is the diameter at which the balls are rejected.
The results of sieve analysis of the ball charges of large mills, quoted by Davis, are in extremely close agreement with those calculated from equation (6.6) and so the general truth of the theory appears to be established. From this it would appear that a definite equilibrium of the size distribution of the balls exists. So all that can be done in practice is to feed replacement balls of diameter dm at the correct rate and to remove the balls smaller than diameter do either continuously or at fairly frequent intervals. The theory of Davis leads to an expression for the size distribution of the balls in a mill but does not give information as in the rate of loss of metal. This matter will be discussed in a later chapter.
https://www.911metallurgist.com/slurry-flow-rate-mill
https://www.911metallurgist.com/ball-mill-liner-design
