Table of Contents
The problems of slope stability in open-cast mines are examined. A criterion, the instantaneous stripping ratio, is suggested for use in the design of pit slopes and as an index of control at all stages of the exploitation of the ore body. This criterion may also be related to safety and to the maximizing of profits.
Two approaches to safe design of slopes, one from the point of view of soil mechanics and the other from the point of view of rock mechanics, are described and critically compared. The effect on slope stability of the regional tectonic stress field is discussed. Explanation is given of the application of the Terzaghi effective stress concept to problems in both soil and rock environments, including possible effects when borehole deformation techniques are used to measure stresses in rock in situ.
The Relation Between Economy of Operation and Slope Angles in Open-Pit Mining
The main object of any industrial enterprise in a free economy is to make a profit. In mining where profits must be made from a wasting capital asset, a further definition of the profit motive is imposed, namely that the economic aim should be to maximize the total possible profit. But since profits deferred for a number of years are not as valuable as profits that are immediately available, it is usual to discount deferred profits at some rate of interest which reflects their current or present value in the hands of the investor. Thus in mining the logical aim can be defined more closely still it is to maximize the present value of the total future profits. In commercial terms the present value represents the market value of the operation as a going concern. Many factors enter into the forecast of current and future profits. They include the volume of production, the price of the saleable product and the cost of production. Current profits can be estimated with reasonable accuracy by the operating engineers; but it is the task of economists and management to assess future trends in the mineral markets and in the economy as a whole, and together with the engineers, they can then estimate the future cost and profitability of the mining operations.
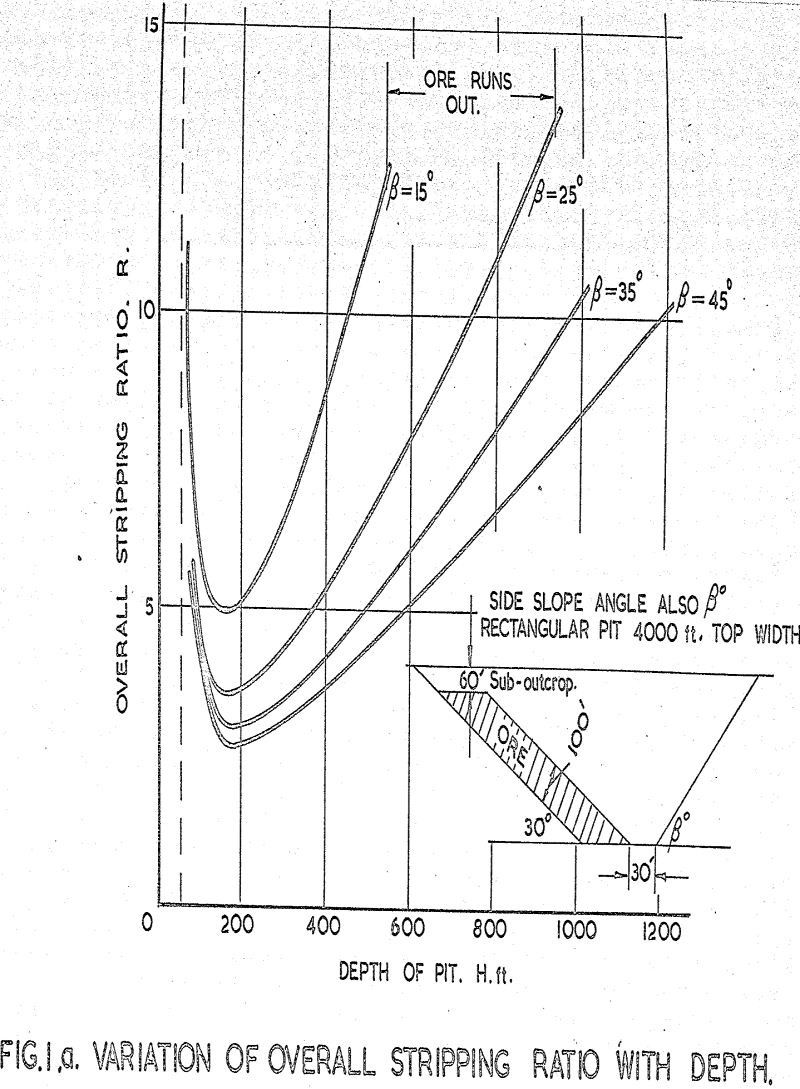
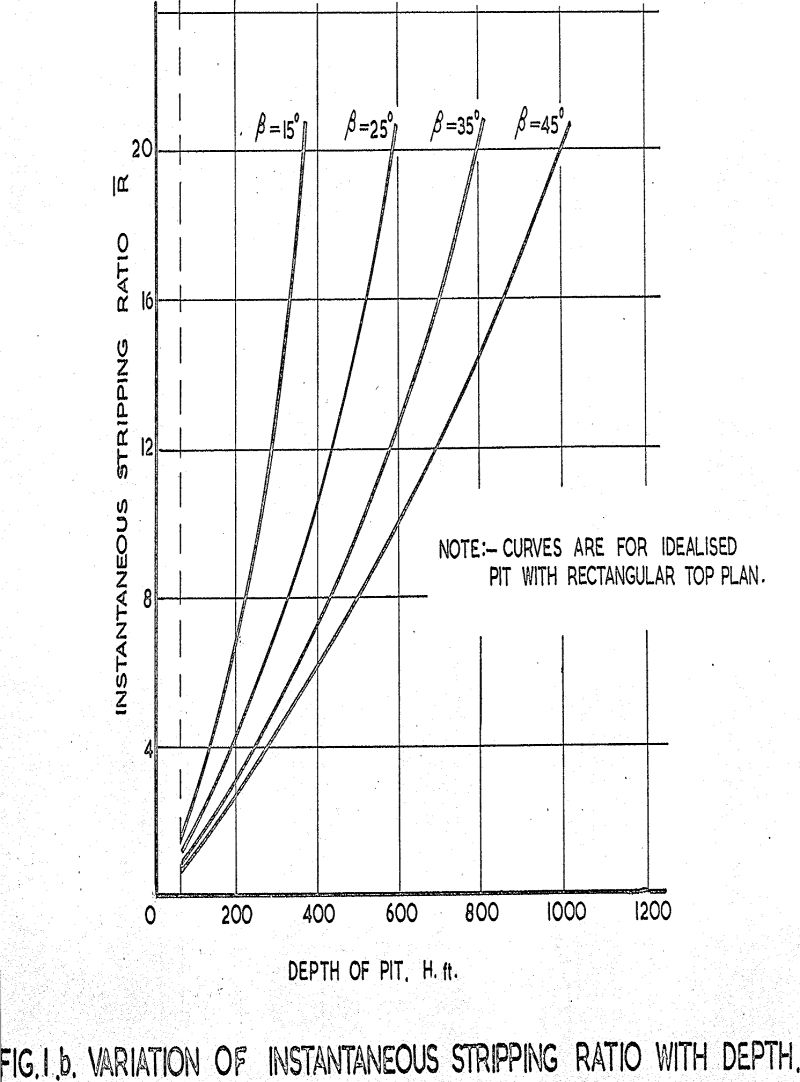
In open-cast mining, the rate of ore production once decided on remains a virtually constant factor, unless a major change in the capital structure of the mine is made. But one factor over which the operator has a considerable measure of control is the ratio of the volume of ore mined to the volume of waste overburden removed and sent to the dump, already defined as the stripping ratio. Unless the ore body is lying horizontally in a flat terrain, the stripping ratio is a function amongst other things of depth. That is as time progresses and the pit becomes deeper, the stripping ratio will increase if the overall slope angles in the pit remain constant.
Safety of Slopes of Pits
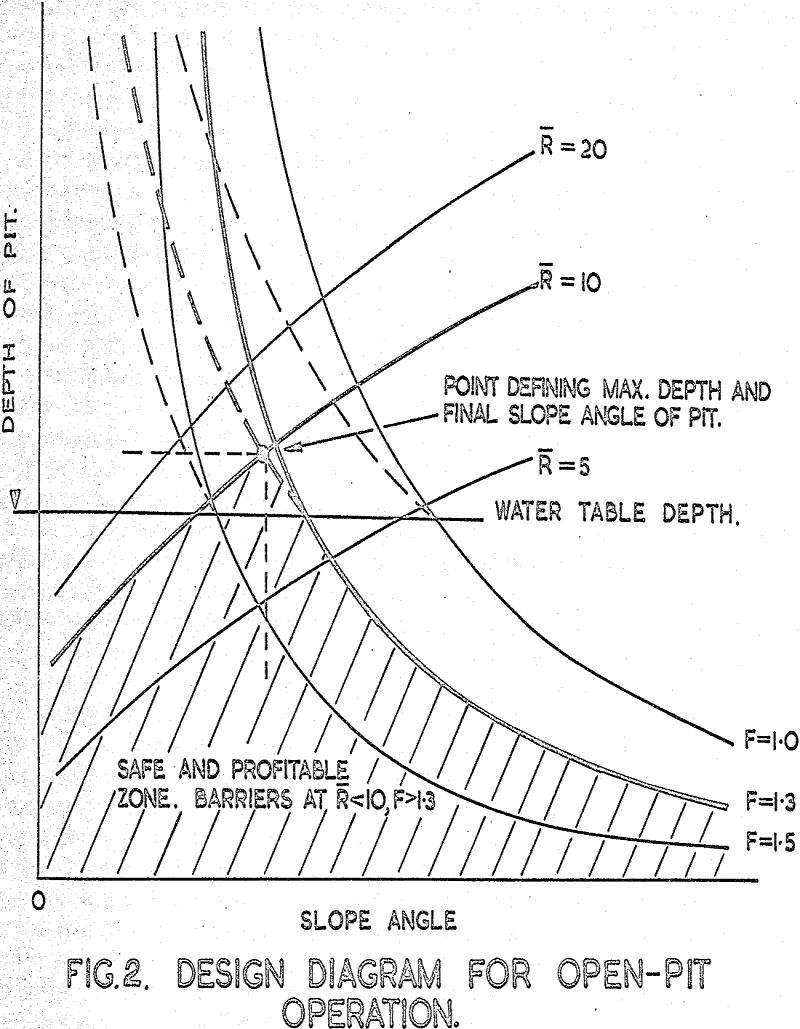
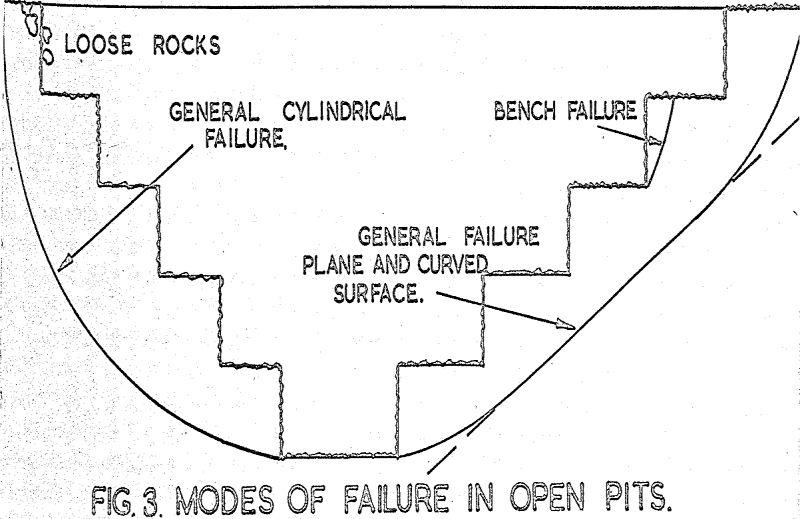
From practical observation it is well known that if an excavation is made in natural ground or soil material the sides can be vertical providing the depth is small. As the depth increases the sides must be battered to avoid collapse: further, if the excavation is deepened to below the water table and seepage water is pumped out of the excavation, a considerable flattening of the slopes is required. These observations suggest that there is one relationship between slope angle and depth for the ground above the water table and another for the material below the water table. The aim of stability investigations for any open pit should be to produce curves of the type shown, which indicate at a glance the economic and safety situations for the pit at any stage in the work.
Another practical observation which appears to have considerable bearing on the stability of slopes in open pits lies in the comparison of slope angles in the pit and on the waste dumps. In one very large pit the safe slope angle determined by past experience lies between 23° and 26°, yet when the same rock material is loosely dumped as waste it stands at a slope of 38°. The reason for this apparent paradox must be sought since it probably has an important bearing on the whole problem of safety of slopes..
Geological Factors Affecting the Pit Slopes
The excavation of a large open pit may be viewed as the artificial production of a slope comparable with the slope of a natural, mountain side. Consequently, examination of the topography and shape of natural slopes in similar materials in the vicinity will assist the engineer, to understand the slope behavior in the pit.
The geology of the materials in the pit should be studied as thoroughly as possible. The general stratigraphy, including dipping and folding of the strata, faults, joint patterns and gouge materials on the joints should be recorded as a continuing operation, starting with the first examination of the ore body. The aim should be to discover patterns in the occurrence and orientation of these phenomena which will enable the engineers to anticipate the behavior of controlling geological structures behind the working, slopes of the pit.
The degree of homogeneity of the geological materials is of great importance. The presence of weak strata, seams, or gouge in harder materials will often be the controlling factors in stability. Natural slopes frequently reflect these features. The engineer should try as far as possible to arrange his operations to work with, instead of against, nature. It should be the continuing aim of the pit engineers to find simple criteria, such as indices of drilling speed or the relative ease of digging, for recognizing such weak conditions in the natural soil or rock. The value of these continuing studies, as an integral part of the mining operation, cannot be over-emphasized.
The Soil Mechanics Approach
The science of soil mechanics may be defined as the understanding of the behavior of incompetent earth materials under the influence of the stresses encountered in engineering practice. The boundary between competent and incompetent material is ill defined. Pits such as Nchanga in Northern Rhodesia, Yallourn in Australia, and the brown coal mines near Cologne in Western Germany clearly lie almost wholly in ‘soils’. The question must be asked, however, whether highly fractured but competent materials, such as the porphyries of the copper deposits in the western U.S.A., can also be considered from the point of view of soil mechanics.
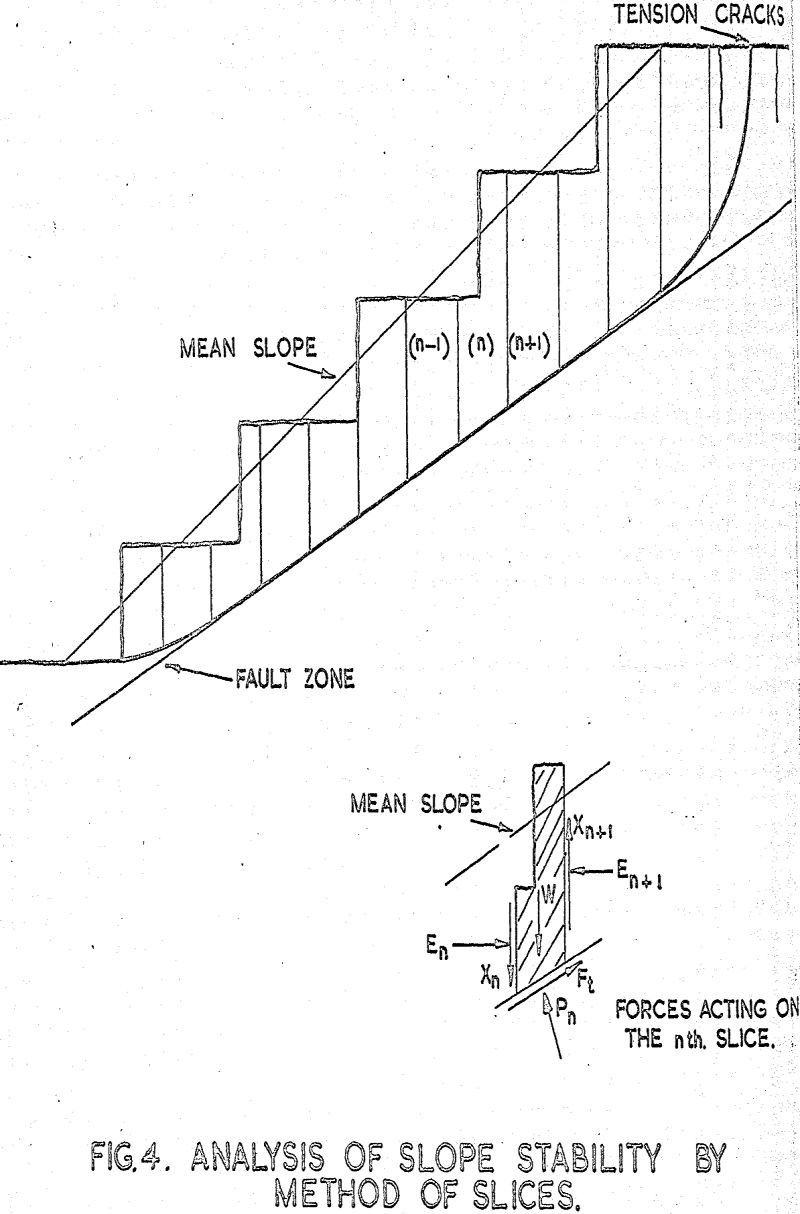
These may be cylindrical, in the case of homogeneous cohesive soils, such as uniform clays, plane for homogeneous non-cohesive soils, such as sands or broken rock, or combinations of planes and curves for mixed materials, particularly when preferred planes of weakness exist behind the slope. The slope is analysed in terms of resisting and disturbing forces or moments. The factor of safety of the slope, that is the least ratio of these forces or moments, is determined for the most critical potential surface of failure. The method of analysis most commonly employed is the ‘method of slices’. The method is an ultimate load design procedure. In structural engineering practice the same approach is referred to as plastic yield design. The computed margin of safety is expressed as a load factor of safety, as opposed to the stress factor of safety used in traditional elastic analysis.
Fluid pressures, such as fissure-water pressures, can contribute nothing to the frictional resistance given by the second term of equation (6). This introduces the important concept of ‘effective pressure’, which is the difference between the total pressure acting normally to the plane of failure and the fluid pressure. If the fluid pressure is denoted u, then equation (6) may be rewritten.
S = c’ + (σ – u) tan ∅’
= c’ + σ’ tan ∅’
where c’ and ∅ are now the cohesion and friction parameters with respect to effective stress, σ’. It can be seen that the value of u has significant effects on S.
The Difficulties of the Soil Mechanics Approach
The principal difficulties of the soil mechanics approach are the estimation of shear strength, and the estimation and measurement of the pore water pressures required for the effective stress analysis. These problems are being tackled in the following ways:
(a) Relationship between normal pressures on the failure plane in the laboratory and in the field.
(b) Shear Along Joint Planes.
(c) Uniformity of Materials in the Slopes.
(d) Taking of Field Samples for Laboratory Tests.
(e) Knowledge of Pore and Fissure Water Pressures.
The soil mechanics approach, presents difficulties which are to be expected in a problem which is as complicated as that posed by open-pit mining. However, none of the difficulties is insuperable and serious attempt is now being made to tackle them. The principal advantage of the soil mechanics approach is that the methods now employed have considerable precedent. There are many published records on the back-analysis of slides which have taken place in various soil slopes in natural and artificial cuttings and banks of all kinds. factorily in these cases as well.
The Rock Mechanics Approach
Rock mechanics is a relatively newly-identified branch of study. It relates to the understanding of the behaviour of competent rock materials under the influence of stresses encountered in engineering practice. The rock mechanics approach to slope stability in open pits has been adopted by one large organisation in the U.S.A. concerned with the mining of copper ores in deep open-cast mines. The pit materials are highly jointed, competent rocks, requiring blasting for excavation.
The approach being adopted by Soderberg and Rausch is on the following lines
(a) The measurement and study of regional ground stresses, including the changes caused by the excavation of the pit.
(b) A geological investigation to locate the weakness and their orientation in the,materials which will form the slopes of the pit.
(c) Analysis to determine the shear strength of the materials, particularly on preferred planes of weakness.
(d) Slope-stability analysis combining the effects of regional stresses and stress changes, the planes of structural weakness and the strength of the materials. This analysis will presumably result in some factor of safety, the precise nature of which has not yet been defined.
Changes in the horizontal stress field behind the slopes due to excavating the pit appear therefore to depend mainly on the geometry of the pit and the nature of the original horizontal stress field. As a first approach these stress changes may be calculated by assuming the material to be elastic and by applying the differential equations of stress equilibrium and strain compatibility. This is likely to prove difficult and a simpler approach would be to study the problem with photo-elastic models. As a refinement, an attempt should be made to determine the stress pattern after the pit is cut, for the case when some plastic flow has taken place.
One danger which can result from disturbing the original stress field might arise in the case where the principal components of regional horizontal stress were significantly different. In this case zones of tensile stress might be generated in the materials behind the slope and shear stresses be developed on planes at 45° to the directions of the major and minor principal stress. This is a case deserving considerable attention but careful thought should be given to the possibility of complete stress relief by local yielding in such circumstances.
The operation of the effective stress principle can be demonstrated by the model, which employs a cylinder of porous rock with a central hole, of the same type as that cut during a rock stress measurement in the field. The whole rock cylinder is simply subjected to a water pressure, the same pressure being exerted on the outer and the inner faces.
Now consider the case of rock stress measurements made in natural material, for example, in a deep mine. Let the depth be of the order of 6,000 feet and the water pressure in confined fissures, back of the face, be equivalent to a head of 5,500 feet. The rock is jointed, compact, competent material but it has a small void volume amounting to 3%. When the first small diameter borehole is drilled, assume that it fails to intersecta joint in the rock, but that it passes within 2 feet of such a joint at a distance of 30 feet from the drilling face.