Several reasons contribute to the wide gap in the industrial application of the academic models. These include: 1) the lack of generality in the model, e.g., the model is limited to certain size ranges; 2) the academic models involve complicated mathematics 3) confusion about the order of the flotation rate, e.g., several authors proposed a first order rate model, whereas the others propagated a second order rate model 4) the use of an unrealistic rigid value, such as the use of a maximum recovery of 100%, which is unrealistic in industrial operations; and 5) the use of graphs that confuse the reader rather than interpret information.
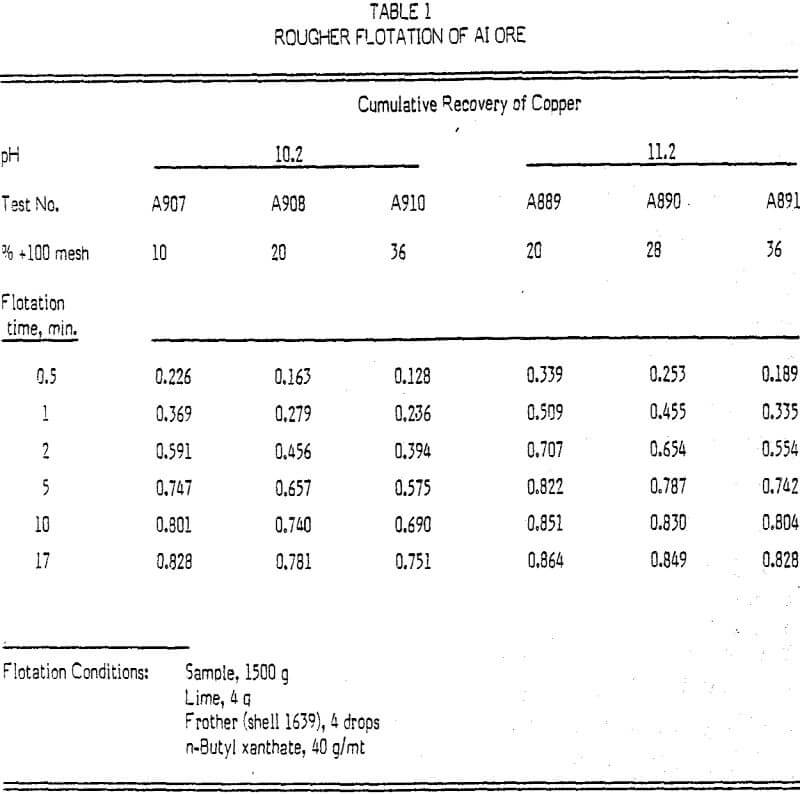
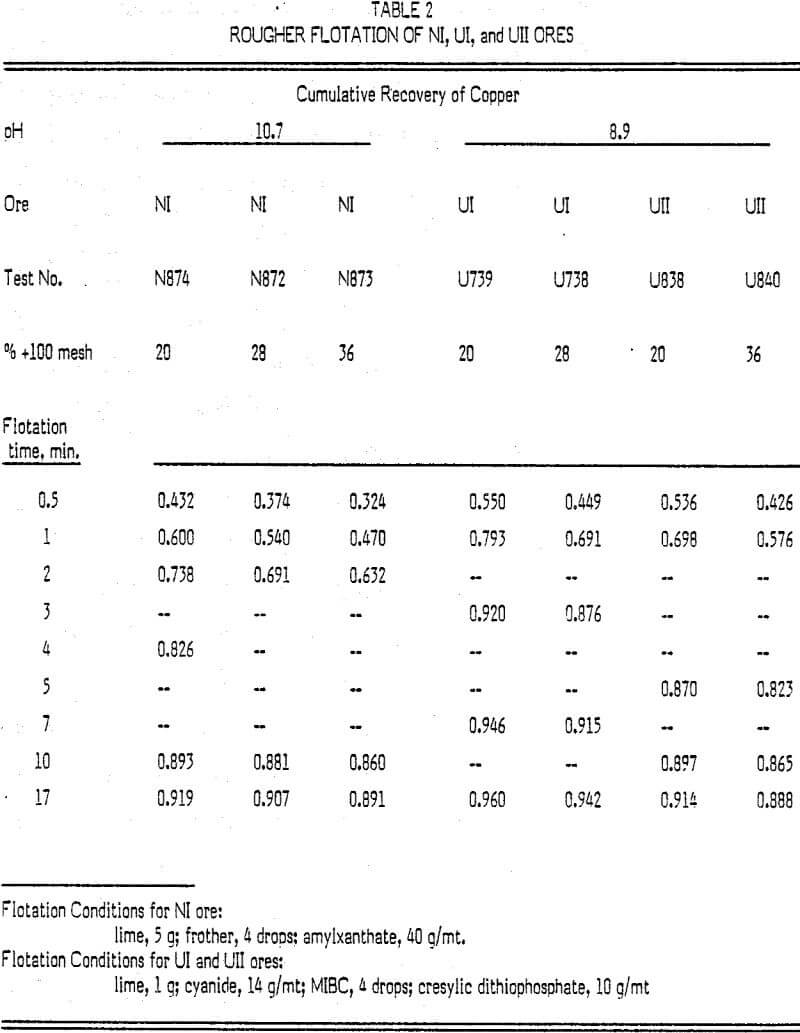
The standard procedure in the laboratory rougher flotation testing was as follows: 1500 g of sample was ground in the presence of lime at 60% solids to a specific grinding requirement. The pulp was then transferred to a 5.8-liter Denver cell. Flotation chemicals were added and the pulp level adjusted to the 4.4-liter level. After conditioning for 30 sec, flotation was started. The froth was collected at intervals which were more frequent in the beginning and less frequent to the end.
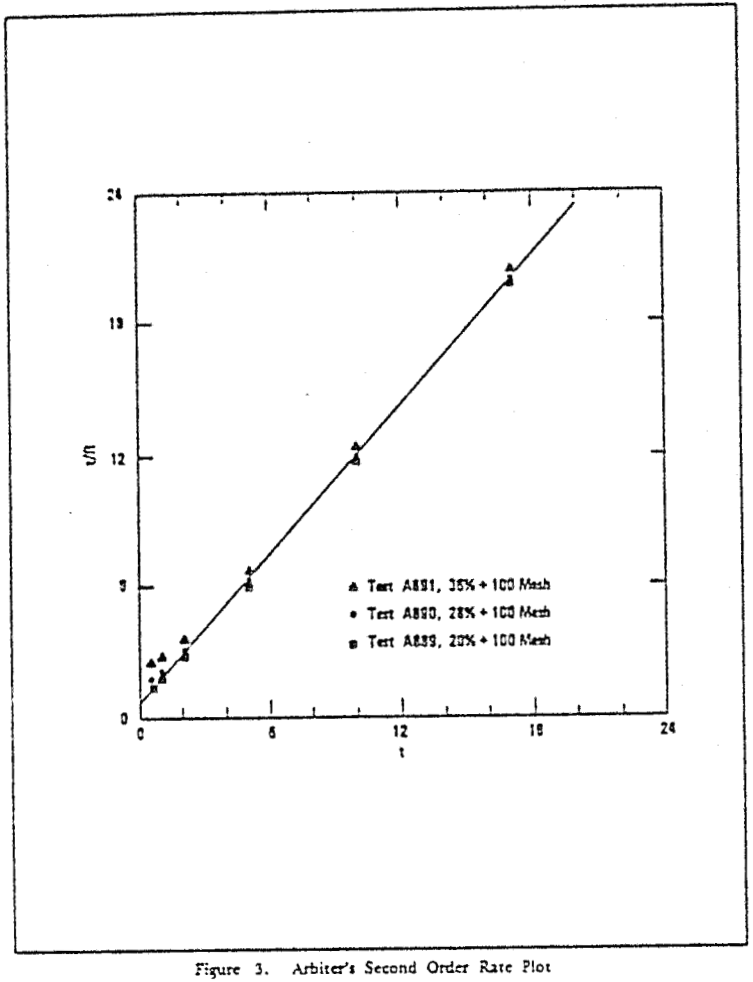
The flotation rate of copper is proportional to the residual recoverable fraction of copper and inversely proportional to the time, i.e.,
dR/dt = k (Ri – R)/t………………………………………………………………(1)
where R is the cumulative recovery of the copper at time t, k is a proportional constant or an intrinsic rate constant, and Ri is the common maximum attainable recovery of copper or an imaginary maximum recovery of copper for a given ore.
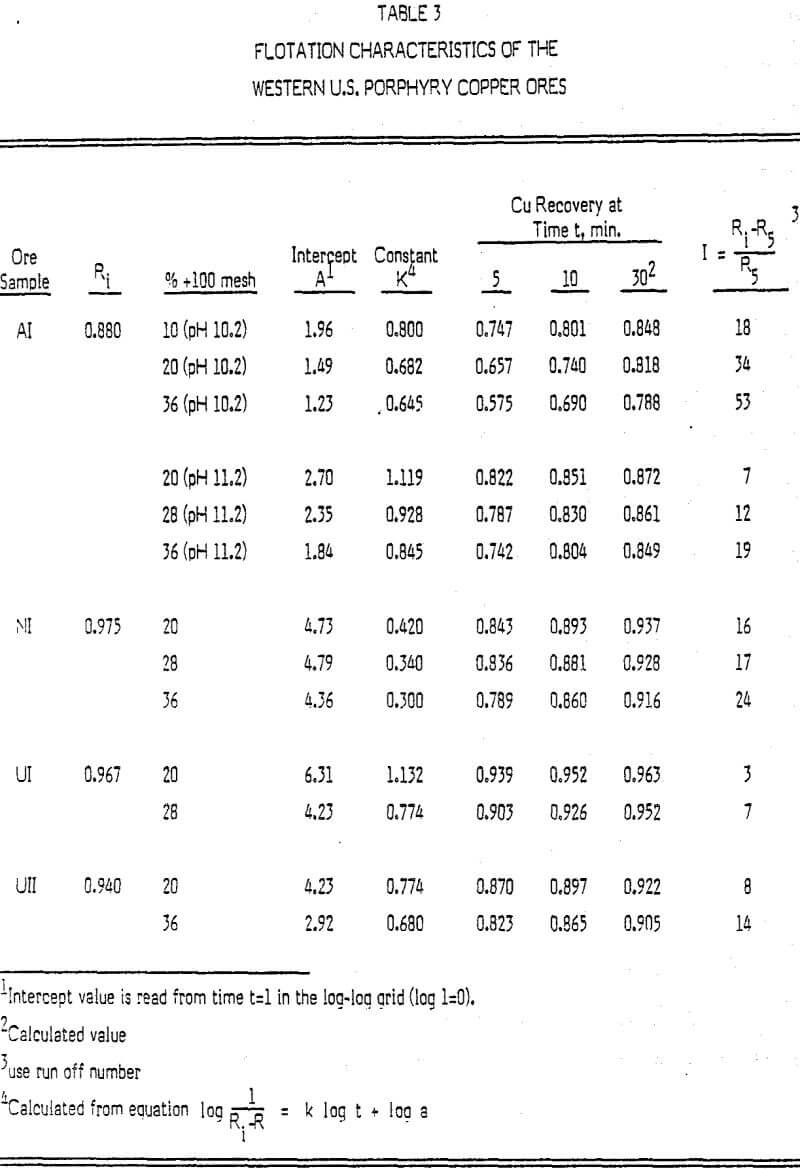
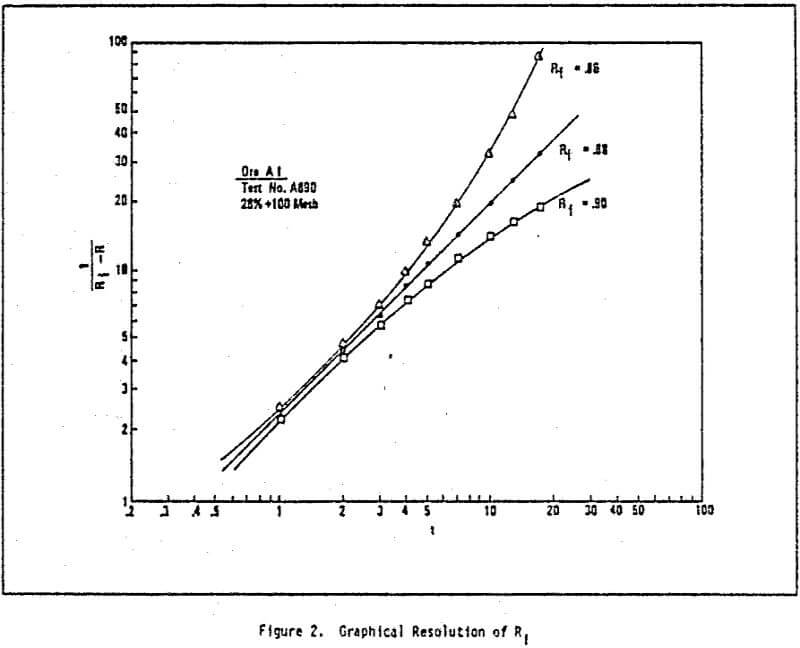
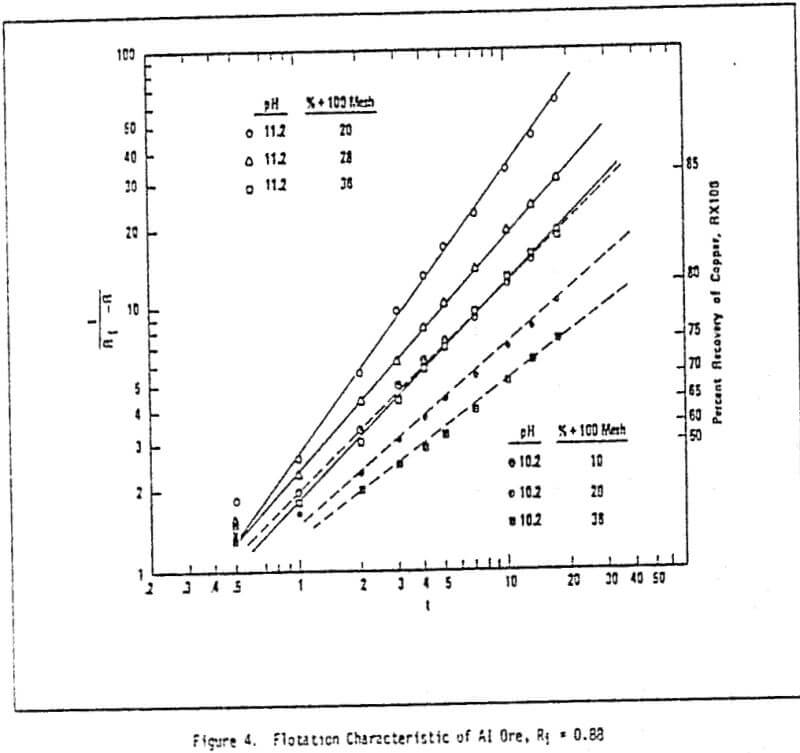
The parameter Ri in equations (1) and (2) is the key parameter of the empirical kinetic model. It is the unknown asymptote equivalent to the maximum possible recovery of the flotable material for minerals). More importantly, it is a unique parameter associated with a specific ore and is independent of the grinding (i.e., change in particle size and particle size distribution), and chemicals (e.g., change in pH, etc.).
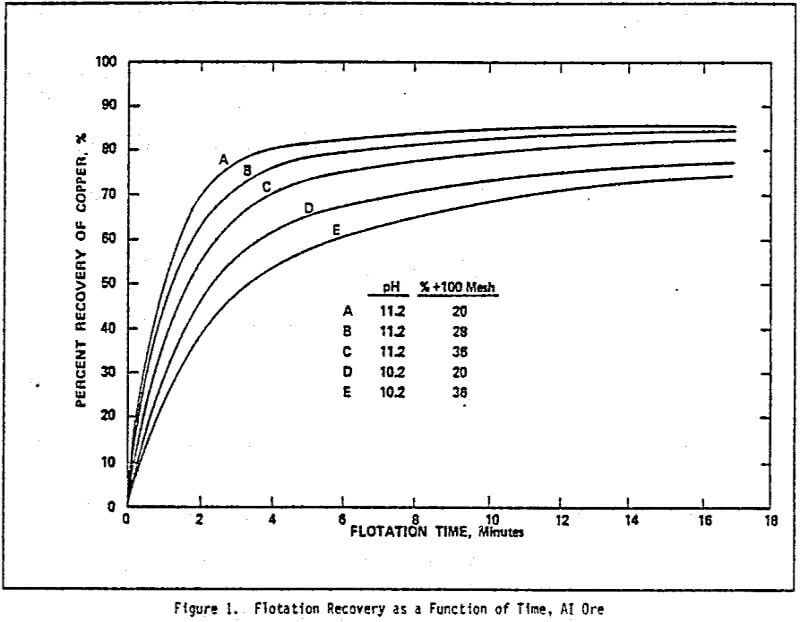
For example, to obtain an 85% recovery of cooper, it requires 9.2 minutes flotation at pH 11.2 for the ore with a grind of 20% over 100 mesh; a change in the grind from 20% over 100 mesh to a grind of 36% over 100 mesh alone, without change in pH, would require an extension of flotation time to 32 minutes. If the pH was changed to 10.2 simultaneously, then the flotation time would be over 100 minutes.
In industrial flotation tests it has been found that the flotation rate processes follow the following empirical rate equation.