The little book on ‘Surface Tension and Surface Energy’ by Willows & Hatschek shows how the elastic film analogy in the study of froth will get one into no end of trouble if not handled with care. It is the characteristic of analogies to break down when pressed too far, though they are useful up to a certain point. This one is no exception. In the case of india-rubber it is obvious that a given weight can only stretch this to a definite extent. To further enlarge the rubber film, an additional weight would be required; while with a liquid film this is not true. Reference to a recent article shows that the measure of surface tension is not when the film breaks but at the instant when the wire is pulled away from AB. If the wire is pulled a great distance without breaking the film, the total energy of the surface is increased, of course, but the energy per unit-area and surface tension are unaffected. Whether or not the film breaks, depends not upon the surface tension, but whether or not there is enough liquid to supply the added area. The difference between a non-aqueous substance and a liquid film is, that in stretching the former the molecules are distorted or separated while in stretching a liquid film molecules come from within the liquid to occupy the new area. According to Devaux the surface tension phenomenon disappears as soon as there is no more liquid to come from within. The same laws apply to surfaces that are allowed to contract. The rubber has a constantly decreasing force of contraction as it approaches its original dimensions, while a liquid film always tends to contract with the same force independently of its size. Now, it is a common practice in demonstrating physical principles to omit certain qualifying conditions until the main features are outlined. This method must be pursued here. The qualifying statement is, that, in the case of a contaminated liquid the film may not “contract with a force independently of its size;” that is, after learning to look upon surface tension as a constant force we must now view it as a variable force. Take, for example, the explanation of the effect of oil on waves. When a small wave is formed on the surface of water the surface is stretched ; for obviously the wavy surface has greater area than the plane surface. Owing to the stretching of the surface the oil film is made thinner so that the contamination due to oil is reduced, and hence the surface tension is increased; this increase in surface tension tending to oppose the production of the wave.
Again, Edser discusses variable surface tension under the heading ‘Stability of a Liquid Film.’ He shows that when a film is on a vertical rectangle equilibrium is impossible unless the surface tension is greater at the top than at the bottom of the film. This is obviously due to the weight of the film itself. For pure water, the surface tension is nearly constant, and therefore, a water film more than two or three millimetres in height cannot be formed. A slight trace of grease will give the water a variable surface tension ; if the surface tension at any point on the film is insufficient to produce equilibrium, the film stretches at this point, and the concentration of grease is diminished, so that the surface tension increases automatically and equilibrium is maintained.
He concludes by saying that the great stability of a soap film is due to the wide variation in surface tension between freshly formed and long exposed parts of the surface and that any stretching of the film, due to insufficient strength, immediately increases the surface tension. Now it seems to me that it is time for us to get away from the idea that low surface tension per se, is necessary for the formation of a froth, for Edser has made it clear that the contamination of the film with something that will give a variable surface tension is the essential. To be sure this amounts to reducing surface tension because contamination of water, with some exceptions, has this effect. The attorney who discoursed at great length upon surface tension and said that the longevity of a bubble was increased by decreasing the contractile drawing force of surface tension, was merely riding too far the willing horse that many of us have ridden so freely.
It is quite easy to accept the statement that soap contaminates water enough to afford a variable surface tension, but it is not quite so clear how a very small fraction of 1% of oil will give the same results, until we have considered adsorption.
Adsorption has been described several times in the technical journals but I believe I am justified in taking it up again and quoting from ‘Surface Tension and Surface Energy,’ because here we find the generalized statement describing adsorption in a liquid and its effect on surface tension. It says: “If the dissolved substance diminishes the surface tension of the solution, an excess of concentration in the surface layer diminishes surface energy. If on the other hand, the solute increases the surface tension the surface energy will be reduced if the concentration in the surface layer is lower than that of the bulk of the solution. This difference in concentration between the surface layer and the bulk of the solution is called adsorption and is a physical fact. The factors tending to produce adsorption are opposed to the factors tending to establish uniform concentration. The final distribution of a solute is the resultant of adsorption and two other effects, namely, osmotic pressure and electric charge. Important qualitative conclusions are drawn from theoretical considerations already developed. A small quantity of dissolved substance may reduce the surface tension very considerably, but it can only increase it slightly. Thus, sodium chloride increases surface tension of water to a small extent; the concentration in the surface layer is accordingly smaller than in the bulk, and the effect of the solute is thus partly counteracted. On the other hand, many organic salts reduce surface tension, and therefore accumulate in the surface layer; so that in extreme cases, the whole of the solute may be collected there and produce a considerable effect, although the absolute quantity may be exceedingly slight.”
Adsorption is of such unmistakable importance that we will refer to ‘The Chemistry of Colloids’ by W. W. Taylor for a different perspective of the same thing. Here I quote freely, for I am not intending to advance my own theories but to bring out what seem to me to be the pertinent physical facts. And here I wish to state that I fear that the premise for my recent calculation of the carrying capacity of the surface of a liquid is not correct. It was an attempt to elaborate on a weak statement in a text-book and hence the calculations themselves cannot be credited.
Adsorption, in its most general sense, implies the unequal distribution of substances at the boundary between two heterogeneous phases: solid-gas, solid-liquid, and liquid-gas. We are concerned just now with only the last.
The surface layer of a liquid is under great compression due to the great difference of the molecular forces on the two sides of the interface and consequently the concentration in the surface of a solution must be different from that in the bulk of the liquid. For just as unequal temperatures in a dilute solution cause an unequal distribution of the solute, so from the same law unequal pressures must also produce an unequal distribution. This pressure (due to surface tension) always, in time, adjusts itself to the minimum, for a component which lowers surface tension is always increased in the surface layer whether the component be present as solvent or solute.
We now have a new principle to apply to a bubble, to wit: on account of adsorption a fresh surface always has a greater surface tension than an old one; thus if it is stretched locally by conditions tending to break it, it is automatically reinforced at that point.
It is now obvious that without adsorption it would be impossible to realize a variable surface tension, for if the solution were contaminated uniformly throughout, a fresh surface exposed by the stretching of the film would have the same energy as the old surface and the ultimate result would be identical with the case cited where pure water was used.
In this argument I have assumed that the contaminating substance is soluble in water. I realize fully that many of the flotation oils are said to be insoluble in water, but I maintain that solubility is only relative, and further, we know nothing about the multiplicity of chemical reactions possible in a pulp which might release contaminating substances that would produce the adsorption phenomenon. If graphite, for instance, acts as a frothing agent, it might have to be treated as a special case and could not be taken as proof that the above arguments are invalid. If the flotation oil is extremely insoluble in, and lighter than, water there would be an oil film at the liquid-air interface and over the liquid film containing adsorbed oil. It might be well at this point to drop the subject of variable surface tension and undertake to get a better idea of the absolute value of these forces. One physicist has spoken of them as being enormous.
As far as surface tension is concerned it is theoretically possible to blow a soap bubble as big as a house.
Take the formula:
(1) P = 4T/r
Where T = pull due to surface tension in grams of a film of one surface and 1 cm. long.
P = excess pressure inside per unit-area, and r = the radius of the sphere.
This formula takes into account the pull on both the internal and external surfaces. It needs no demonstration, as it is derived in the same manner as the old familiar formula used in calculating the thickness of boiler-shells, etc.
In case of a liquid drop or a bubble submerged in water, the formula is:
(2) P = 2T/r
Now let us use these formulae to make a little study of the mathematics of a bubble to see how much a variation of surface tension and external pressure amount to when numerically expressed and see if Mr. Callow’s argument is good.
He states: “The bubbles being generated under a hydraulic pressure varying from 15 to 40 inches, on rising above the water burst by reason of the lower surrounding atmospheric pressure.” This pictures the emerging bubble as expanding like a bladder when suddenly inflated by increased internal, or decreased external, pressure, and is a misconception. To make the steps more simple we will first study the bubble in air and then when submerged.
Assume 1 cc. of free air taken in form of a sphere
(3) V= 4.2r³ = 1
r= 0.620 cm.
Now suppose this air to be enclosed in a liquid film in air where the liquid-air surface tension is 70. The new radius can be calculated by the application of Boyle’s law, which is, that the pressure varies inversely as the volume, where absolute pressure is of course understood. The free air is, in round numbers, under a pressure of 1000 gm. per sq. cm. and a surface tension of 70 dynes per cm. exerts a pull equivalent to weight of approximately 0.07 gm. per cm. of length.
The proportion used to calculate the new radius is:
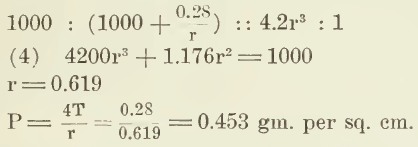
The second term of equation (4) is the only one that contains a function of surface tension, and since it is of such small numerical value, it is plain that any variation of surface tension has very little to do with the radius of an individual bubble in air. Even when the surface tension varies between zero and a maximum, as in (3) and (4), the change of radius is, in fact, too slight to be calculated on the slide-rule—only from 0.620 to 0.619 cm. It is interesting to note that P has a value of 0.453 gm. per sq. cm. which equals 0.006 lb. per sq. in. This is the order of magnitude of the forces that cause a spray above the froth.
Suppose again that the bubble is 1 cm. below surface. We then have:
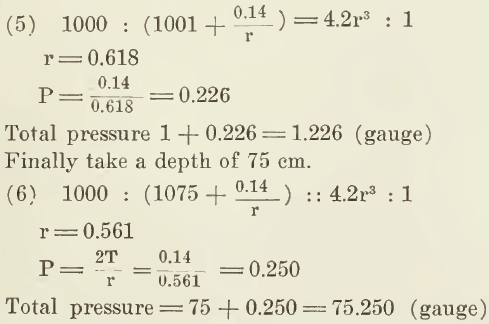
These results are shown in the appended table:
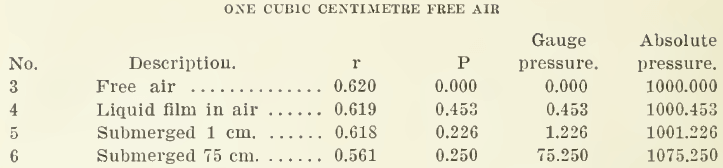
Column r shows that a bubble emerges with an infinitely small change of radius. In fact the change is on the side of decrease because of the surface film being doubled. Now, since there is practically no expansion or contraction upon emerging from the liquid, it seems to me that “low surrounding atmospheric pressure” has nothing to do with bursting Mr. Callow’s bubbles. Of course it is well known that if a gas bag is burst under water the gas remains under confinement: whereas if it is burst in air it is evanescent, but it is necessary for the metallurgist to study the texture of these bags.
Since a bubble does not expand, how are we going to account for “4-inch bubbles”? By coalescence (unless electrification plays a part). Sometimes they cohere but do not coalesce. When they coalesce the large one robs the small one because pressure varies inversely as the radius (see Equation 1). The little one ‘pumps’ its gas into the large one. We shall have to learn how to control coalescence.
Viscosity is another important factor that must be considered along with variable surface tension and coalescence. It is not surface tension that breaks bubbles, but it is blows upon a surface that lacks viscosity or toughness and variable surface tension, that cause rupture. They rupture easily on account of lack of friction of the molecules. With low friction a blow is likely to cause the molecules to be separated a distance at which surface tension phenomena disappear before other molecules have time to come from below and reinforce the area with their greater surface tension.
The books all emphasize the importance of great superficial viscosity and small internal viscosity for the persistence of a froth. It is said that alcohol which has a superficial viscosity less than the internal viscosity, when mixed with superficially viscous liquids, will neutralize the relative surface viscosity and make frothing impossible. Hence the practice of adding a few drops of alcohol to check frothing in pharmaceutical work. We know that tannin sometimes interferes with flotation work and also that it may form a colloidal solution with water. May we not add that alcohol and tannin are deterrents because adsorption is checked on account of internal viscosity produced by them ?For, without adsorption, one of the leading factors tending to produce a stable froth is nullified, that is, variable surface tension.
My best thanks are due to Dr. W. B. Anderson, professor of physics in the College, for his helpful suggestions and critical reading of these notes.
