Table of Contents
The extreme variability in gold mineralization in drill core is revealed through the detailed sampling experiment. This variability is that naturally present on the smallest scale that can be found by fire assay. With samples of substantially larger volumes, less variability would be found. Most of the variability is associated with among-feet rather than within-feet sample intervals. Because of the extreme variability, most of the gold is in a few samples; one-half of the value is in 3 percent of the samples.
For statistical analysis of these data, logarithms of the assays are better than untransformed assays. Although assaying reliability was good, practice assaying of typical ore would have improved the experimental results. An additional experiment, described in Appendix B, should be done to yield results specifically applicable to mine practice.
Purpose of Work
For several reasons, most gold mines are difficult to sample. The amount of gold is small compared with the amount of rock; a deposit with one troy ounce of gold per short ton contains only 34 parts per million of gold, or 34 grams per metric ton, or 0.0034 percent. Moreover, these 34 parts per million are rarely, if ever, spread evenly throughout the ore, but are sporadically distributed. For example, the gold in a 1-ounce-per-ton deposit might be in small but easily visible particles 1 cubic millimeter in size, corresponding to cubes 0.04 inch on a side. Then, each particle would weigh 0.019 gram; a metric ton of ore would contain only about 1,800 particles, or 6 out of every million particles of this size.
If the distribution of gold in ore is known a suitable plan for sampling this particular ore can be developed. As a means of investigating the distribution of gold in ore, a sampling plan was devised that would introduce as few complications as possible in the mine sampling, in the sample preparation, and in the assaying. The plan was tested by sampling ore from the largest U.S. gold mine, the Homestake mine, in South Dakota.
This Bureau of Mines report describes the methods of sampling, sample preparation, and assaying. A statistical analysis of the assay values is the basis for extracting as much information as possible from these numbers. Conclusions are drawn applicable to ore of the same type in the Homestake mine and elsewhere. Finally, suggestions are made for additional work in the Homestake mine that would test new methods for mine-sampling practice.
This report on data from the Homestake mine is part of a larger study on sampling of gold mines. A previous report on sampling was published on a South African gold mine work is being done on other gold mines in the United States. Each deposit has particular sampling problems as well as its similarities with the other deposits.
Mine Location, Geology, and Production
The Homestake mine, Lead, S. Dak., the largest U.S. gold mine, has produced about 96 million tons of ore containing some 28 million ounces of gold, an average of 0.29 ounce per ton.
The most recent accounts of the geology of the mine, are McLaughlin and Noble, who includes complete references to other articles. The ore is localized in parts of the Homestake formation of Precambrian age. The Homestake formation, originally a low-grade iron formation, has been metamorphosed and intensely and intricately folded. Its present composition is mainly chlorite, cummingtonite (a calcium, magnesium amphibole), and quartz, with sub¬ordinate ankerite, garnet, iron sulfides, and other minerals. Typically, the ore contains 0.33 troy ounce gold per ton; 8 to 10 percent of sulfide minerals, mainly pyrrhotite; and a little silver.
At the Homestake mine, extensive sampling is done of the ore in place, broken ore, mill feed, and mill products. The ore in place is sampled by several different methods for the purposes of grade control and selective mining, including pillar location and stope widths. The practical application of this report is mainly to the part of the sampling done by diamond-drilling.
Experimental Data
Hole Drilling
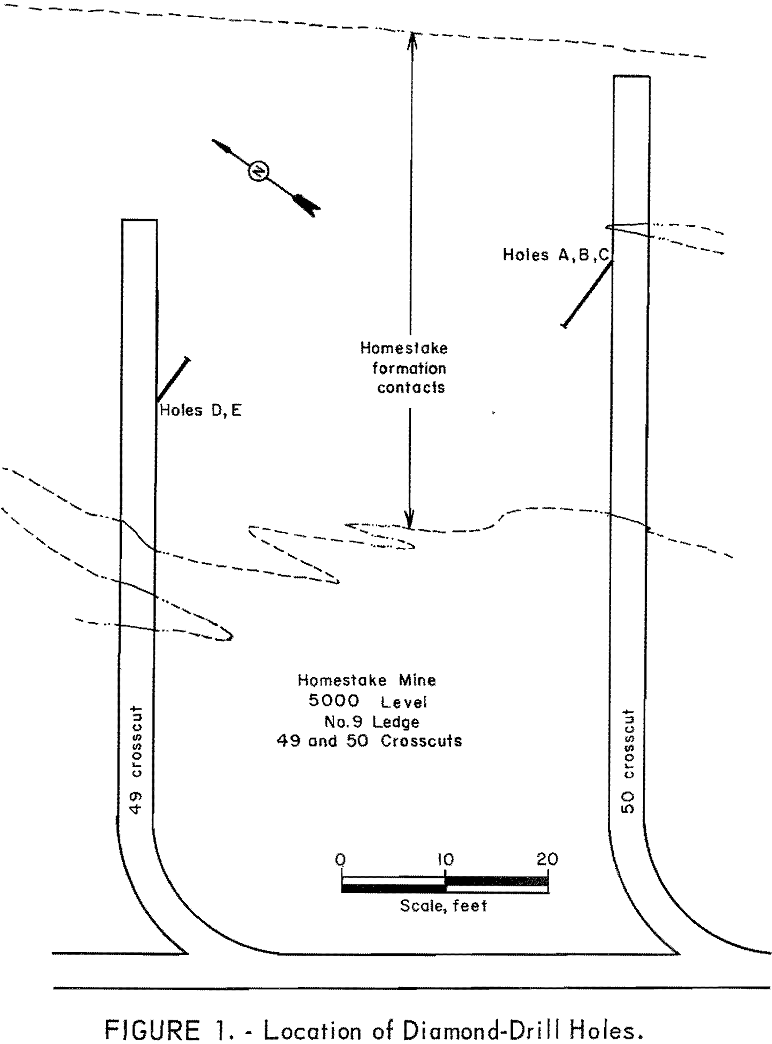
The material used for the experiment consisted of 56 feet of EX core from five diamond-drill holes, ranging in length from 5 to 15 feet. The holes were bored entirely in ore in the Homestake formation at typical locations selected by G. C. Mathisrud, assistant chief geologist, Homestake Mining Company. One objective of the sampling was to compare the variability in gold content and gold distribution on a scale of a few inches with that on a scale of a few feet; therefore, three holes spaced 3 inches apart were bored in one crosscut (No. 50, fig. 1), and two holes spaced 6 inches apart were bored in an adjacent crosscut (No. 49, fig. 1).
The holes were bored by the Homestake Mining Company, while one of the authors (G. S. K.) observed the drilling, logged, and boxed the core. Core recovery was above 95 percent except at and near the collars of holes, where core was lost in collaring the holes and in drilling through friable rock loosened by blasting for the crosscuts.
Core Sampling and Assaying
The method of sample preparation is summarized in figure 2. The drill core was cut transversely with a diamond saw into pieces 1 inch long to obtain samples for assay, weighing about
one assay ton (29.1667 grams). Thus, no variation was introduced through splitting pulverized material or screening out coarse gold that could not be ground. The average volume of the assayed samples was 9.35 cubic centimeters; the average specific gravity was 3.14. The volume standard deviation was 1.31 cubic centimeters, stemming mainly from core losses in drilling, but partly from technical difficulties in sawing the core.
Two random pairs of adjacent 1-inch pieces, a total of 4 potential samples out of a possible 12, were selected from each of the 56 feet of drill core. These adjacent samples were selected to obtain a measure of variability on as small a scale as possible to compare with the variability on larger scales. In this manner, 224, or one-third of the possible inches, were selected. The sample from 1 selected inch was lost in drilling, yielding 223 samples and 111 pairs sent for assay.
The selected samples were crushed with a Chipmunk-type jaw crusher and pulverized to about minus 200 mesh in a Braun pulverizer. Before each sample was

crushed and pulverized, the apparatus was carefully cleaned to minimize contamination from sample to sample.
The selected samples were assayed randomly to avoid systematic variation that might have been introduced through such a factor as variation in furnace runs. Assaying was done at the Reno Metallurgy Research Center of the Bureau of Mines by John Boylan, assayer, under the direction of Howard H. Heady, chief of technical services. Four samples were lost in assaying, reducing the number of assay values to 219 and the number of pairs to 108.
Statistical Analysis
Various techniques of statistical analysis were applied to the assays and to natural logarithms of the assays. Logarithms were taken to stabilize the extreme variability in the data so that the sources of variability in the data could be better understood. For convenience, the statistical analyses were performed with an electronic computer; however, they could have been done readily by desk calculators because the data were not too numerous and the calculations were not too elaborate.
The results of the statistical analyses are described as follows: First, the frequency distributions are presented to indicate the extreme variability and skewness present. Second, the main purpose of the investigation, to determine the sources of variability in the data, is explored in some detail. The practical application of the variability present to interpret grades and reliability of grades is taken up, and finally, the reliability of the assaying is assessed.
Frequency Distributions
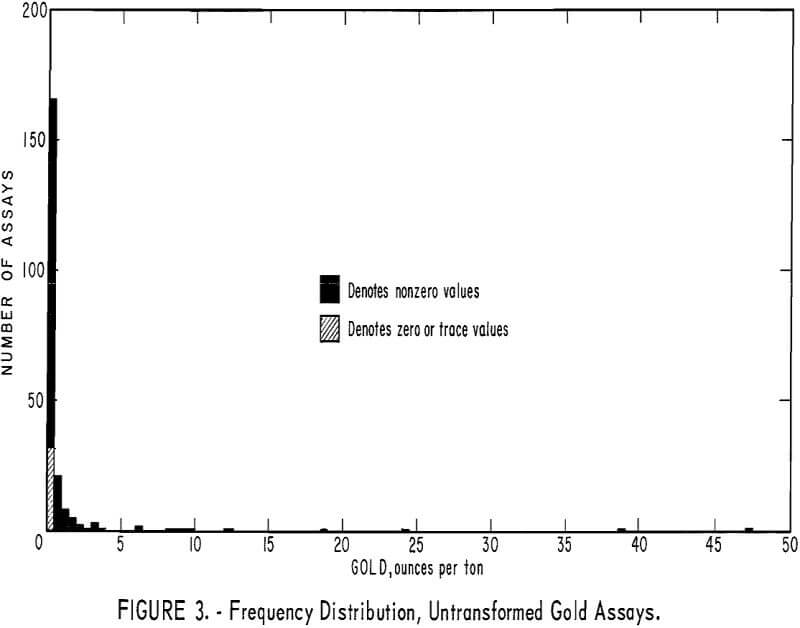
Figure 3, a frequency distribution, indicates that the 219 assay values are highly skewed; 167, including 32 zero or trace values, fall in the interval from 0.0 to 0.5 ounce per ton. (The samples with assays reported as zero or trace contained an amount of gold below that which could be accurate determined by fire assay.) A frequency distribution of the natural (Napierian) logarithms of the assays was also made (fig. 4). This second distribution is truncated because the 32 assays recorded as zero or trace cannot be transformed; this distribution is perhaps compatible with a truncated normal distribution. The degree of truncation for logarithms of gold assays is much less from some other deposits (for example those in South Africa), because they are richer or because the sample volumes are larger.
Sources of Variability
In table 1, the variability in these Homestake gold data is compared with that in other typical assay data. The comparison is made by listing coefficients of variation (ratio of standard deviation to mean), The table shows that these Homestake data are extremely variable, with standard deviation almost four times the mean, even in comparison with other gold data characteristically more variable than base-metal data. At least part of the extreme Homestake variability results from the small sample volumes taken; the pattern
of variability is presented by the data lists in the appendix. Some correspondence exists among holes; high assays in one hole, or a zone of low or trace assays from samples in a quartz lens, are generally repeated in about the same position in the adjacent hole or holes. These results suggest that the samples have at least a small area of influence, and that the assaying was consistent.
For examination and comparison of the sources of variability in the gold assay data, the statistical method of analysis of variance was used. The details of analysis of variance calculations, given in statistical texts, are not reviewed here; the purpose of the method is to isolate the amount of variability from different sources, to determine where most of the variability lies, and to calculate how much of the variability can be explained by known sources and how much remains unexplained. Tables 2 and 3 are analyses of variance for natural logarithms of gold assays and for

untransformed gold assays. The two tables isolate the variability from different sources; both are constructed as follows. The total amount of variability listed on line seven is partitioned into four pieces, each from a particular source. The first line gives the variation from hole to hole; this variation is further divided in lines two and three into that associated with the two groups of holes in the two crosscuts. Line four gives the variation from foot to foot, within holes, line five gives the variation between sample pairs within feet, and line six gives the variation within paired samples.


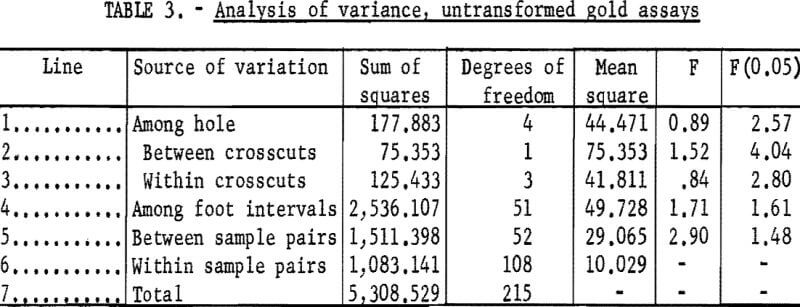
Tables 2 and 3 show that within a bore hole, as the distance between samples increases, so does the variability. Thus, the between-pair variability is larger than the within-pair variability, because the observed F-values of line five (mean square of line five divided by mean square of line six, equal to 1,69 and 2,90) are larger than the corresponding F(0.05) value of 1.48. Also, the among-foot variability is larger than the between-pair variability, because the observed F-values of line four (mean square of line four divided by mean square of line five, equal to 5.15 and 1.71) are larger than the corresponding F(0.05) value of 1.61. Moreover, much of the variability within a hole is associated with a scale of the order of one foot, because the among-foot variability (sum of squares of line four divided by sum of squares of line seven) is almost 70 percent of the variability of the logarithmic data and is almost 50 percent of the variability of the untransformed data. Thus, most of the change in gold content occurs from foot to foot. The distribution of gold from foot to foot in all of the five holes is shown in figure 5.
There is little variability among the holes, either within or between crosscuts. Because the holes were bored across the grain of the orebody (perpendicular to the strike of the foliation), little variation might be expected among holes in one crosscut, but the small variation between crosscuts is somewhat surprising. Tables 2 and 3 show that the among-hole variability is no larger than the among-foot variability, because the observed F-values of line one (mean square of line one divided by mean square of line four, equal to 0.26 and 0.89) are smaller than the corresponding F(0.05) value of 2.57. Moreover, the between-crosscut variability is no larger than the among-foot variability because the observed F values of line two (mean square of line two divided by mean square of line four, equal to 0.03 and 1.52) are smaller than the corresponding F(0.05) value of 2.82. And, the within-crosscut variability is no larger than the among-foot variability because the observed F values of line three (mean square of line three divided by mean square of line four, equal to 0.35 and 0.84) are smaller than the corresponding F (0.05) value of 2.80. It is inappropriate to compare the between-crosscut variability and the within-crosscut variability because the sample sizes are unequal and because the degrees of freedom are too small. However, the mean square values on lines two and three show that these two kinds of variability are more or less of the same size (excluding the rather small between-crosscut mean square for the logarithmic data).

All of the assays were made on samples with the volume of a 1-inch cylinder. If the samples had been larger (assuming perfect mixing and splitting before assaying), the assays would have been less variable. In the extreme case, if all samples had been combined into one sample before assaying, the mean value of 1.25 should have been obtained. To determine the change in variance with an increase of sample volume, the means and standard deviations of sample volumes corresponding to cylinders 2 and 4 inches long were calculated by combining the appropriate results from the 1-inch-long cylinders actually assayed. The results, listed in table 4, are for doubling and quadrupling the sample volume; no significant change is noted in the variance because the basic unit of variation is the 1-foot interval. If the relation of sample variance to samples of volumes of 1-foot-long cores or more could have been calculated, it would very likely have shown a decrease in variance with larger volume.
Estimation of Metal Grade
Generally, the main purpose of mine sampling is to estimate grade of ore. Although the samples in this study were not taken specifically for this purpose, they may be used to estimate metal grade, thus illustrating methods that might be employed in practice. With estimating grade, inquiry into the reliability of estimate may be done by means of confidence limits, defined as
x ± t s/√n
where x is the mean of statistically independent assays; t is a statistical value (tabulated in statistical texts) depending on the number of assays; s is the estimated standard deviation; and n is the number of samples. Close estimates, corresponding to narrow confidence limits, can be obtained in one or both of two ways: (1) by having small values of s, implying a uniform metal distribution, large sample volumes, or precise sampling and assaying; (2) by increasing n, the number of statistically independent assays, which also decreases the size of t.

Table 5 presents the means, standard deviations, and confidence limits for the five diamond-drill holes and for all holes combined, statistical independence assumed. Although all of the means for the individual holes are numerically different, those for holes A, D, and E are similar; those for holes B and C are higher only because of a very few high assays. Because the drill-hole means are based on a statistical sample of the 1-inch cylinders in each hole, different means would be obtained if other cylinders had been assayed. Therefore, it is meaningful to inquire whether the observed differences among the five means merely reflect the statistical fluctuation present. The appropriate analysis of variance compares the among-hole variation (line two) with the within-hole variation (line five) in tables 2 and 3. Because the calculated F values are lower than the F(0.05) values, it was concluded that there is no evidence that the means differ for any reason other than statistical fluctuation.
The five diamond-drill holes were bored in an orebody selected as typical by the Homestake geological staff. The Company assay data from this part of the mine indicate ore with a grade near that of the mine average of about 0.33; yet the average grade in each of the five holes is higher. Based on the details of the Company assay records and on visual examination of the crosscuts, some evidence shows that the holes were collared in higher grade than average material. However, the confidence limits do not clearly indicate whether the five holes in fact cut higher than average grade ore, or whether their apparent highness in grade is due merely to statistical fluctuations and that the ore in the holes was in fact typical of that in the mine.

That most of the gold is in only a few of the samples is clearly displayed by ordering the assay values and plotting cumulative metal grade against number of samples. The resulting graph (fig. 6) shows that one-half of the samples with the lowest grades contain virtually no gold, whereas only 6 of the highest grade samples (3 percent) contain one-half of the gold. A complementary graph (fig. 7) indicates the consequences of arbitrarily cutting high assays. Inclusion of the eight highest assays is necessary to raise the mean above 0.5 ounce per ton to the final figure of 1.25; therefore, these are key assays that any valid method of averaging for valuation must take into account. If the assays above an arbitrary value of 1.209 ounces (corresponding to a value of $25 based on gold at $20.67 per ounce) are cut to 1.209, the grade follows the dotted line to an end point of only 0.31. Although in practice cutting assays may be justified, for example, to allow for dilution in mining or as a safety factor, no cutting was done in the present study because the core sampling was appropriately randomized; no significant changes resulted from sample preparation; and the assaying was reliable. The subject is introduced to show how misleading the practice of cutting high assays can be unless a careful analysis of the consequences is made.
The distinction between high- and low-assay values is explored in still another way in table 6, which contrasts the statistics obtained by separating samples above and below 0.5 ounce. As pointed out before, the large number of samples permits a good estimate of grade with narrow confidence limits for the low-grade material; but for the high-grade material, too few samples with a high standard deviation result in a poor estimate of grade with wide confidence limits.
A difference between the high- and low-grade material has been the main point demonstrated in this section. The worst estimates are associated with high grades, accompanied by large standard deviations and small number of samples, because of the formula


x ± t s/√n
Yet, for these high grades the best estimates are required. In Appendix B, suggestions are given for further work that could establish practical sampling procedures making use of the material in this section.

Appraisal of Assaying
The reliability of the assaying may be appraised in three ways; by comparing qualitatively the uniformity of the results for samples with gold found, blank samples with zero or trace results, and samples lost; by comparing the assay results among furnace runs; and by comparing the assay values of selected and unselected sample pairs.
In table 7, the samples from each furnace run are classified according to gold found, blank, or lost. Because of 13 furnace runs, a Chi-square calculation to examine the uniformity of the results has 24 degrees of freedom. The calculated Chi-square value is 76.

In table 8, the among-furnace-run variance is compared with the within furnace run variance by use of the F statistic. The observed F value is 1.2, with 12 and 206 degrees of freedom.

Lastly, in table 9, the variance of assays of randomly selected sample pairs (fig. 2) is compared with the variance of assays of samples that can be paired because they were physically adjacent, but not selected pairs, in the drill cores. The comparison indicates the general uniformity of the assaying because the variance of selected pairs is 10, whereas that of unselected pairs is 3.5.

From these three tables, the conclusion may be drawn that regardless of some difficulties, particularly in the first two furnace runs, the overall assaying was excellent. It would have been worthwhile to have supplied the assayer with Homes take ore for preliminary test runs, even though he was thoroughly experienced in gold assaying. This precaution may be useful in any work requiring the assaying of new material.
