Table of Contents
In most routine experimental work on products and processes, methods of operation and product evaluation are established from accurately controlled laboratory tests. With particular emphasis on the pelletization of fine iron ore concentrates, standardized procedures of laboratory production and product testing have been established at Cleveland-Cliffs Iron Co. Research Laboratory at Ishpeming, Mich. A program of this nature was used for investigating the agglomeration characteristics of various iron ore concentrates. The factors which control the process were studied and subsequently controlled for these investigations.
The extent of the bonding phenomena and the consequent strength of fired pellets is governed by some of the following firing conditions and properties of the unfired pellet: 1- mineralogical composition of the pellet. 2- particle packing within the pellet. 3- particle size range, of the minerals comprising the green pellet. 4- maximum temperature to which the minerals are exposed and the retention period at this temperature. 5- the rate of attainment of and rate of recession from the maximum temperature. 6- the gas composition of the atmosphere in which the pellet particles are fired, and 7- the high temperature chemistry of the mineral particles and the additives of the pellets.
If the atmosphere of the fired iron ore particles is not of homogeneous composition, differential agglomeration will come about within the pellet because of particle chemistry differences. Hematite, magnetite, and the lower oxides of iron definitely possess different properties of agglomeration. If some of the iron minerals are contiguous to reducing substances during firing, the agglomeration characteristics will differ from particles fired in an ambient atmosphere that is oxidizing in nature.
Shaft furnace firing of green iron ore pellets is carried out by the placing of wet pellets on the top of a shaft hearth containing pellets in the process of being fired. As the charge descends into the shaft by gravity, the wet pellets are fired by a countercurrent stream of combustion and heat transfer gases. Varying temperature zones within the furnace perform the following consecutive operations on the descending wet pellets: 1—drying, 2—preheating, 3—firing to a maximum temperature, and 4—cooling.
The regions of different temperature zones within the furnace shaft can be varied by operational controls, but a specific zonal region can also be a function of the high temperature chemistry of the ore pellets. If pellets contain an intrinsic fuel, magnetite or an additive which can exothermally oxidize with the gases, a hot firing zone can literally be floated within the shaft when relatively low temperature gases are allowed to ignite the pellet burden and maintain continual combustion within the descending charge. In this manner descending pellets of magnetite can be ignited with oxidizing gases of 1000°C and a zone of burning pellets can be established that is 1300°C in temperature. The position and maintenance of this zone gives rise to a longitudinal temperature gradient within the furnace shaft, which consequently describes the changes of pellet temperature with time.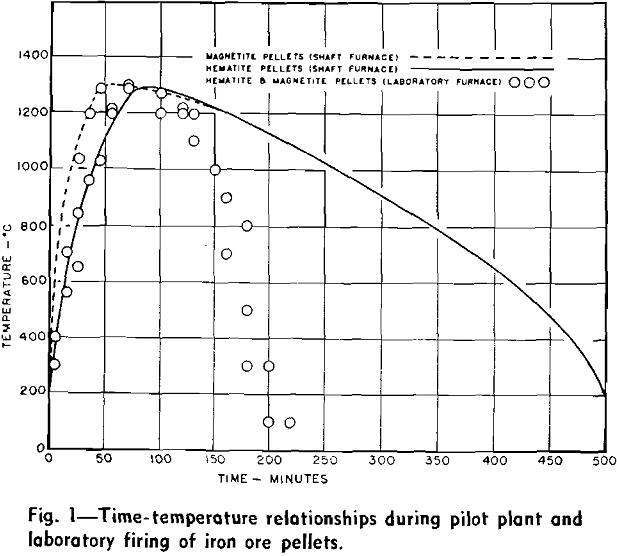
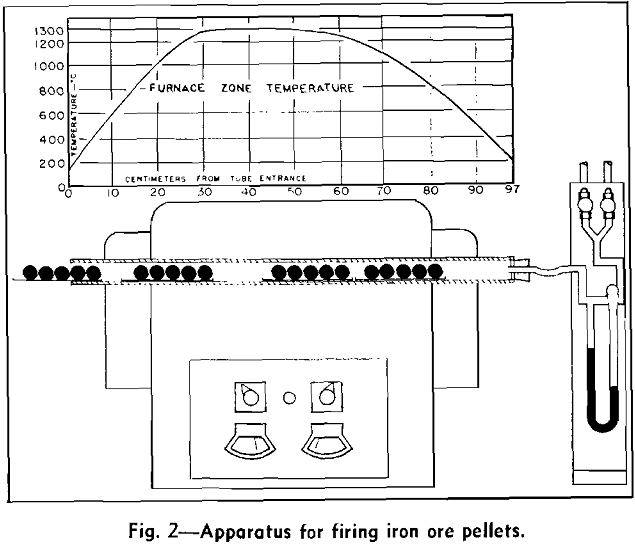
Laboratory Procedure for Firing Pellets
Apparatus consisted of an electrical, globar combustion tube furnace equipped with provisions for passing gas through the tube at controlled flow rates. Nichrome boats which served as the pellet-charging devices were admitted through the open end of the combustion tube, passed countercurrent to the gas stream, and removed through the upstream end of the tube. The boat charge consisted of five wet pellets, each of which was about 35 g in weight and 28 mm in diam. These were formed in a laboratory balling drum by use of procedures described by Tigerschiold and Ilmoni. The drum products were stored in sealed containers and retained for the subsequent firing tests. To minimize pre-drying effects, green pellets representing a specific balling drum product were taken from the containers and placed on the boat approximately 1 min before the actual firing operation.
During operation of the laboratory apparatus pellet-laden boats were admitted one by one into the combustion tube and moved periodically through the tube so that pellets could approach the consecutive temperature changes of shaft furnace pellets.
These discrepancies were tolerable. It would have been impractical to allow laboratory pellets to cool for 10 hr, and the slight variations of the heating rates were of a small order when contrasted to the normal variations of heating rates within a shaft furnace. The results of the laboratory tests were to be relative rather than absolute. For this reason the shaft furnace firing schedule was approached but was not attained.
Pellet Quality Determinations
The quality of fired pellets can be determined by different materials tests to denote the toughness, hardness, and compressive strength. Each of these relates a measure of pellet particle coherency. Iron ore pellets should be able to withstand the crushing forces imposed by furnace and stockpile stacks and the impact and abrasive forces imposed by conventional iron ore handling and shipping. The physical properties that make it possible for pellets to endure these forces are generally related, although not def-
initely. Brittle pellets can conceivably withstand great compressing loads, yet will shatter remarkably from impacts. Tough pellets, likewise, can be comprised of coarse particles which readily abrade from the surfaces. For these reasons, each specific strength property was individually tested by the use of standardized materials test procedures. These were the crush, impact, and abrasion tests used to denote pellet strength, toughness, and hardness, respectively.
Strength is a measure of ability to endure stress. In the case of slow diametric compression of spherical material, stress is a function of sphere size and compressing force. When like-size spherical pellets are subjected to a slow diametric force, the strength and maximum unit stress are directly proportional to the crushing load. Consequently the pellet strength designated herein was approximated from a measurement of the maximum load imposed on an individual pellet, or the extent of the compressing load which caused the pellet to crush.
The abrasion test was developed to find a means of expressing the relative resistance to abrasive action offered by the surfaces of pellets. This abrasive action was caused by inter-pellet rubbing induced by pellet contact and movement in a small rotating drum.
The impact test was developed for determining the toughness of the pellets or the relative resistance to subdivision from impact forces. These forces were imparted by dropping the pellets successively from predetermined height to a solid steel plate surface.
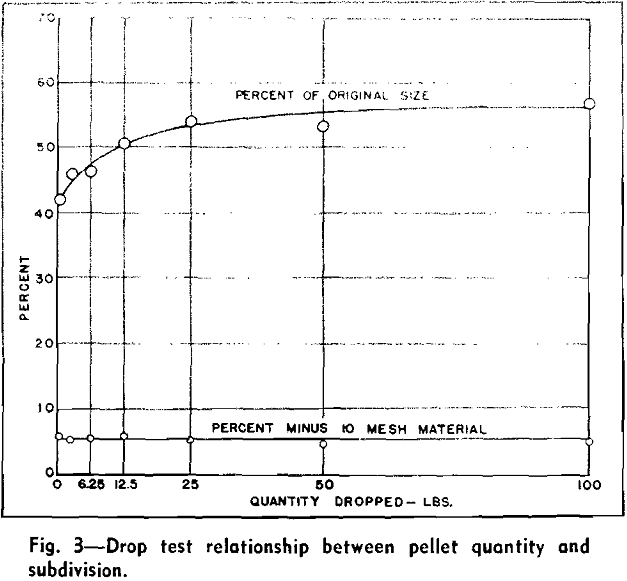
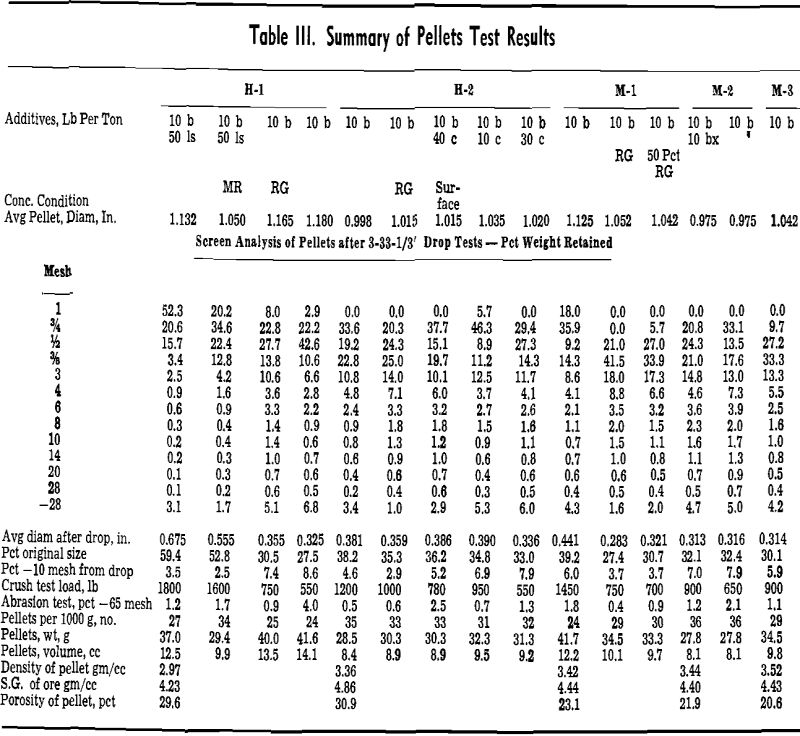
A strength index, or the percent of the original particle size, was computed from the screen analysis
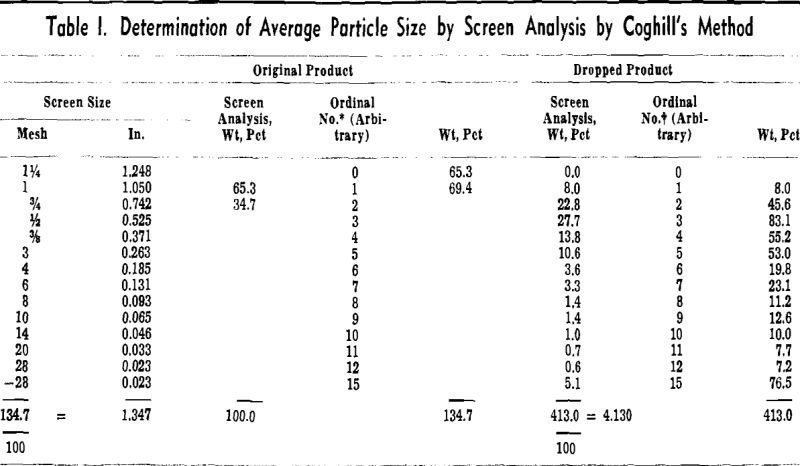

of the pellets before dropping and the screen analysis of the pellets and fragments after three drops.
Several tests were conducted to determine the mass effect of the drop test and to determine the reliability of results procured from a specific test. Approximately 700 lb of pellets of a uniform quality were thoroughly mixed for these tests and varying quantities were cut out from the entire sample. These quantities consisted of two 100-lb portions, two 50-lb, two 25-lb, two 12.5-lb, two 6.25-lb, and eight 1000-g portions.
The most expedient method of measuring the degree of particle coherency within an iron ore pellet is the crushing test. A specific test carried out as a measurement of value, such as the crushing strength of fired pellets, is only as good as the degree of reproducibility of the test.
Results of Laboratory Pelletizing Tests
The laboratory tests were carried out on five different iron ore concentrates, designated as M-1, M-2, M-3, and H-1, H-2. M-1 and M-3 represent two different concentrates of natural magnetite produced from magnetic concentration circuits. H-2 and M-2 represent concentrates of artificial hematite and artificial magnetite produced by roasting iron sulphides under different atmospheric conditions. H-1 represents a flotation concentrate of specular hematite.
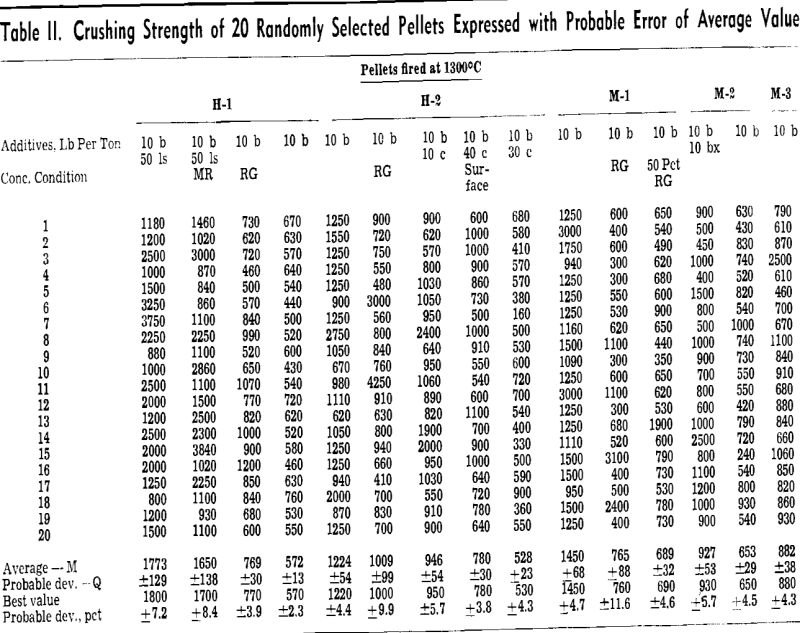
Prior to balling, the ore concentrates were blended in the dry state with ½ pct by weight of bentonite and, in certain instances, with various quantities of other pulverized additives. These blends were further mixed with about 10 pct water and each mixture used as the laboratory balling drum feed.
The apparent detrimental effect of internal carbonaceous matter in iron ore pellets was evident from the decreasing strength properties of H-2 pellets containing increasing quantities of internal coal. Pellets containing 2 pct coal on the exterior, however, appeared to have greater strength properties than pellets containing lesser amounts of coal internally. This demonstration indicated that within pellets containing internal coal, gaseous diffusion lagged behind heat transfer, and carbon abstracted oxygen from the ore rather than from the hot gases.

