Circuit analysis can be used to evaluate the overall effectiveness of various configurations of unit operations in mineral and coal processing circuits. This powerful tool, has regretfully seen only limited application in the analysis of coal processing circuits. Strictly speaking, this method can only be applied if particle-particle interactions do not influence the probability that a particle will report to a particular stream. In other words, the partition (or Tromp) curve should remain unchanged during variations in the characteristics of feed stream. This assumption is generally valid for dense medium separations. This may also be a reasonable assumption for water-based processes such as spirals provided that the changes in feed characteristics are not too large. In fact, circuit analysis will always provide useful insight into how unit operations should be configured in a multi-stage circuit even if the exact numerical predictions are not completely accurate.
Consider the one-stage unit operation shown below. The concentrate-to-feed ratio is given by:
C/F = P…………………………………………………………………….[1]
As a result, the mass of particles of a given property reporting to either the concentrate (C) and refuse (R) streams can be calculated as follows:
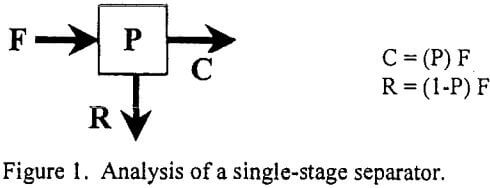
where P is a dimensionless probability function that selects particles to report to a given stream based on their physical properties. For density-based separations, the probability function can often be estimated from an S-shaped transition function commonly referred to as the Lynch-Rao (1975) equation, i.e.:
![]()
in which X is the SG/SG50 ratio and α is a sharpness index. Note that the specific gravity cut-point (SG50) is represented by a value of X=1 at which P=0.5.
The slope of the probability function evaluated at X=1 can be used to represent the separation efficiency of the process. The slope is obtained by taking the derivative of the concentrate-to-feed ratio at X=1. For the Lynch-Rao (1975) equation, this gives:
![]()
However, efficiencies of dense medium separators are more commonly reported in terms of an Ecart probable error (Ep). Ep values may be calculated directly from the probability function using the expression:
Ep = SG50 (X25-X75)/2………………………………………………………[4]
where X25 and X75 are the defined at P=0.25 and P=0.75, respectively. Therefore, the following approximation may be used in this case:
![]()
Now consider a similar analysis of the rougher-cleaner circuit shown below.
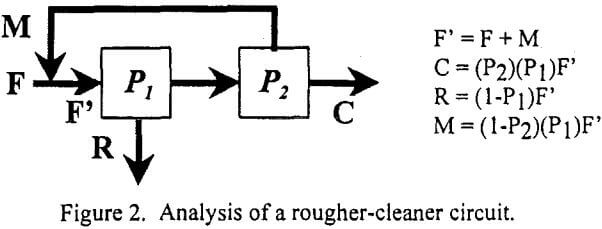
By simple algebraic substitution, the concentrate-to-feed ratio (C/F) for this circuit can be calculated as:
C/F = P2P1/(l-P1+P1P2)……………………………………………………….[6]
If the probability function (P) is assumed to be the same for both separators, then the separation efficiency for the rougher-cleaner circuit is:
![]()
Using the Lynch-Rao (1975) equation and noting that P=0.5 at X=1, the following relationship may be obtained:
![]()
Likewise, for the case involving Ep values, the following approximation will also hold:
![]()
According to this analysis, the separation efficiency (defined by the slope of the circuit partition curve) of a rougher-cleaner circuit should be 1.33 times that of the single-stage circuit.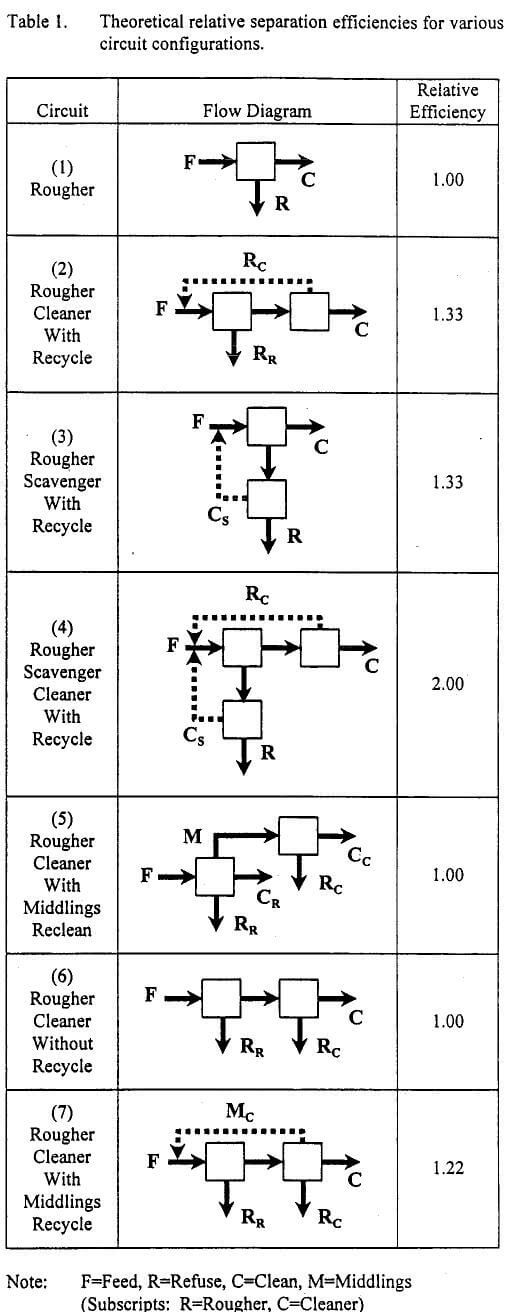
The relative efficiencies of other circuit configurations can be evaluated by circuit analysis using the same approach. Several of these are summarized in Table 1. As shown, the standard rougher-cleaner (Circuit 2) and rougher-scavenger (Circuit 3) configurations each have efficiencies 1.33 times greater than the single-stage process. Note that the rougher-scavenger-cleaner (Circuit 4) configuration incorporating three stages has an efficiency that is twice that of the single-stage process.
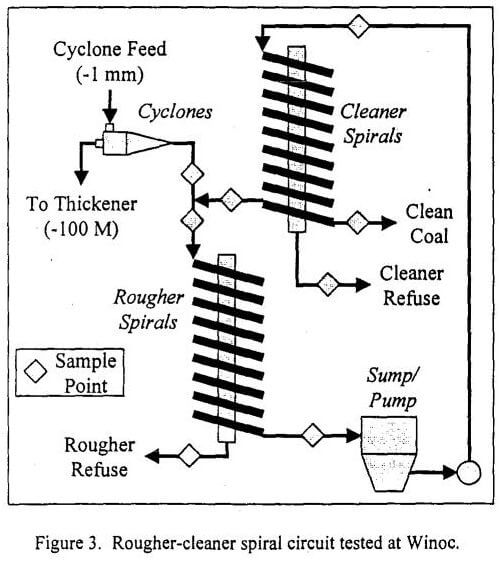
The most common multi-stage spiral circuit used in industry today is the rougher-cleaner configuration (Circuit 5). However, unlike the circuits discussed above, the cleaner spirals are used to treat only the middlings from the rougher spirals. The clean coal streams from both spirals are combined to produce an overall clean product, while both reject streams are discarded. The circuit is normally configured so that no cleaner middlings are produced and no products are recycled. Surprisingly, circuit analysis indicates that this configuration is no more efficient than a single-stage unit. In fact, no improvement in efficiency is obtained even when both the rougher concentrate and middlings streams are passed to the cleaner spirals (Circuit 6). According to circuit analysis, the only configurations inherently capable of improving separation efficiency are those which have product streams that are recycled back to the feed of a previous stage. These recycle streams are shown as the dotted lines in Table 1.
The results of the linear circuit analyses should not be taken to imply that traditional multi-stage spiral circuits have no value. The primary advantage of these traditional circuits is that they provide an effective means for reducing the specific gravity cut-point (SG50) below that which may be achieved using a single-stage spiral. This issue, which is not addressed by conventional circuit analysis, will be discussed in greater detail in a future publication. Furthermore, the “preferred” configurations identified by circuit analysis are not practical for spiral circuits due to large circulating loads and the excessive number of spirals required.
Despite the practical shortcomings of recycle streams, the final configuration (Circuit 7) included in Table 1 does appear to merit further study. In this circuit, both the concentrate and middlings products from the rougher unit are passed to the cleaner unit. The clean stream from the cleaner unit is taken as final product, while the cleaner refuse is combined with the rougher refuse and discarded. The middlings stream from the cleaner spiral is recycled back to the head of the rougher unit. As shown in Table 1, this configuration is capable of an efficiency that is approximately 1.22 times that of the single-stage circuit. While not as efficient as a “true” rougher-cleaner circuit, this configuration substantially reduces the amount of material that must be recycled. In fact, this configuration was found to be the only practical circuit capable of simultaneously improving separation efficiency while reducing cut-point.
 |
 |
