Table of Contents
The method given above is difficult to apply when solutions containing soluble cyanides of zinc and other metals require to be titrated. “ A white flocculent precipitate occurs at a certain stage, probably consisting of simple (insoluble) cyanide of zinc, formed by decomposition of the soluble double cyanide:
K2ZnCy4 + AgNO3 = KAgCy2 + ZnCy2 + KNO3
This precipitation occurs long before the whole amount of potassium has been converted into the soluble double salt of silver (KAgCy2), for the solution after the appearance of the flocculent precipitate, still gives the Prussian blue precipitate with acidulated ferrous sulphate.” Bettel suggested the addition of an excess of caustic soda, and the iodide indicator, titrating with silver nitrate. This gives the sum of the free cyanide, hydrocyanic acid, and part of the double cyanides. Part of the zinc potassium cyanide is decomposed by the alkali, sodium and potassium zincates and free cyanide being formed. The greater the excess of alkali the more complete the reaction would be. Compound cyanides, such as ferrocyanides, sulphocyanides, &c., are not decomposed by caustic soda, so that their cyanogen is not included in the estimation. Owing to the action of mass, none of these actions are absolute, and the estimation is only approximate. The determination does not appear to be of much practical value.
Metallurgists found that the amount of free cyanide shown by this method varies with the dilution. Thus a sump solution was found by titration to contain 0.04 per cent. KCy. On adding an equal bulk of water, it appeared to contain 0.05 per cent. KCy (instead of 0.02 per cent.), and on diluting with two volumes of water, it showed 0.04 per cent. KCy instead of 0.013 per cent. Goyder also observed that a solution of 1 per cent, of crystallised double cyanide of zinc and potassium appeared to have one-thirtieth of its cyanogen as free cyanide, and on diluting to 250 volumes (0.004 per cent. K2ZnCy4), the whole of the cyanogen appeared to be in the state of simple cyanide. The potassium cyanide set free by the action of the alkali is doubtless available, both to dissolve gold and to keep silver cyanide in solution. In any case, it seems quite likely that the free cyanide shown by simple titration represents the cyanide available for the dissolution of gold, provided that the alkalinity of the mill solution is made equal to that of the solution when it is tested in the laboratory.
It is proposed by the following methods of analysis in order to determine:
(1) The total cyanide.
(2) The total amount of “protective alkali”—that is, the free alkalies and alkaline earths, together with half the monocarbonates,
(3) The ferrocyanides.
(4) The zinc.
(1) Take 50 c.c. of the solution. Add excess of NaHO and a little KI solution. Titrate with AgNO3 till there is a distinct permanent yellowish cloudiness.
Result = T c.c. AgNO3
(2) Take 50 c.c. of the solution. Add excess of K4FeCy6 solution. Then run in 2 T c.c. AgNO3. Add phenolphthalein and titrate with N/10 nitric acid till colourless.
Result = p c.c. N/10 HNO3
If an excess of barium chloride is added before this test is made, the result gives the alkalies and alkaline earths only.
(3) Take 50 c.c. of the solution. Add p c.c. N/10 nitric acid; then add 2 T c.c. AgNO3, one drop of K2CrO4, and continue adding AgNO3 until there is a permanent red coloration.
Result = n c.c. AgNO3. (Total amount added.)
(4) Take 50 c.c. of solution. Add 10 c.c. N/10 Na2CO3. Run in 2 T c.c. AgNO3. Shake well. Add phenolphthalein, and then add N/10 HNO3 till colourless. Add 1 c.c. more acid, shake up, and add N/10 Na2CO3 till the clear solution is faintly pink. Add excess of K4FeCy6, and titrate the strongly coloured solution with N/10 HNO3 till colourless.
Result = s c.c.
(5) Repeat No. 4, but adding n c.c. AgNO3, and shaking, instead of 2 T c c.
Result = t c.c.
If the standard solution of AgNO3 contains 13.05 grammes per litre, then the following are the factors:
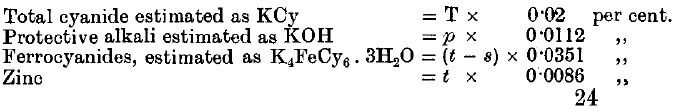
The total amount of cyanogen in a solution, whether present as simple or double cyanides, may be estimated by boiling with an excess of oxide of mercury and water, when all the cyanogen is obtained as cyanide of mercury and the metals pass into oxides. The cyanide of mercury is then precipitated by nitrate of silver, with the precautions recommended.
Estimation of Gold and Metals in Cyanide Solutions
The amount of gold in the solution is usually determined by evaporating a known bulk to dryness in lead basins, or in porcelain basins with the addition of litharge mixed with the liquid before evaporation is commenced. The determination is finished by reducing the lead by fusion in a crucible with charcoal, and cupelling the lead button. Gold can also be determined as follows :—Add an excess of a solution of AgNO3, filter, reduce the precipitate with zinc and hydrochloric acid ; filter, dry, cupel and part the button.
The amount of zinc and other heavy metals present may be determined by concentrating the solution by evaporation, adding an excess of sulphuric acid, and heating until “ almost all the sulphuric acid has been expelled. The residual mass is then free from cyanogen. It is dissolved in water, if necessary with the addition of hydrochloric acid, and the oxides determined by the usual methods. This way is not adapted for cyanide of mercury, as a little of the metal would escape with the fumes of the sulphuric acid.” J. E. Clennel decomposes the cyanogen compounds by boiling with hydrochloric acid and chlorate of potash. The metals are then determined by the ordinary methods of chemical analysis.
Detection and Estimation of Sulphides in Potassium Cyanide
In view of the marked effect produced by soluble sulphides in checking the solution of the gold, it is sometimes desirable to test for them in samples of cyanide, although it is seldom necessary to make exact determinations.
The most delicate test is to add a solution of nitro-prusside to the cyanide solution. The most minute trace of alkaline sulphide is shown by the appearance of a brilliant purple colour. Nitroprusside are formed by adding nitric acid to a solution of ferrocyanide of potassium.
Dr. Loewy’s method for the estimation of sulphides in cyanide solutions is to add nitro-prusside of soda, which gives the violet colour. He dissolves 2 grammes of the sample of cyanide to be tested in 100 c.c. water, and compares it with a solution of cyanide of similar strength free from sulphides. He then adds 1 c.c. of a solution containing 5 percent, of sodium nitro-prusside and a very little cyanide to each solution, and then adds a solution of sulphide of soda of known strength to the pure cyanide until the violet colour is of the same depth in each. The calculation of the result is then simple. The method is applicable to solutions in which the amount of sulphur lies between 0.0005 and 0.0015 per cent. The solutions are adjusted to bring the sulphur within these limits.
Estimation of the Reducing Power of Cyanide Solutions
This is more important than the estimation of sulphides, as the solvent action of the solution depends on its oxygenating power, or the reverse. The methods adopted are to add an excess of sulphuric acid, and either to titrate with potassium permanganate (Clennel’s method), or to add an excess of permanganate and titrate back with sulphocyanide (Bettel’s method). In the first case the end point is denoted by the first appearance of a permanent pink colour, and in the second case by its final disappearance.
Estimation of Oxygen in Working Cyanide Solutions
It is of great importance to be able to determine the proportion of free or available oxygen in mill solutions. One method, devised by A. F. Crosse, is based on Thresh’s method of estimating oxygen dissolved in water.
Another method, proposed by Prof. Prister, consists in boiling off the air contained in a solution, collecting and measuring the gases in Lunge’s nitrometer, and removing the oxygen by means of a strong solution of pyrogallate of potassium made by dissolving pyrogallic acid in caustic potash. The residual gas (nitrogen, &c.) is again measured, and the difference consists of oxygen.
By Crosse’s method the amount of oxygen per litre in certain cyanide solutions was found to be as follows: Solution from Siemens-Halske process before precipitation, 4.65 to 4.69 mgrms.; tap-water, 7.7 mgrms.; the same tap-water, with 0.2 per cent.
KCy and a little ferrocyanide, 7.6 mgrms.; solution as pumped on to a leaching vat, 6.3 mgrms.; the same solution as run from the vat thirty hours later, 0.6 mgrm.; and the same from the end of the zinc boxes, 0.3 mgrm.
Estimation of Bromo-cyanogen
An excess of hydrochloric acid is added, and this is followed by the addition of an excess of potassium iodide. Iodine is liberated, the quantities being those shown in the following equation:
BrCN + HCl + 2KI = HCN + KBr + KCl + I2
The iodine is estimated by titration with sodium thiosulphate in the usual way.
Effect of Thiocyanates on Metallic Gold
This has been investigated by H. A. White, who found that potassium thiocyanate, though inactive by itself, would dissolve gold if mixed with various oxidising agents, such as potassium permanganate, ferricyanide of potassium, dilute nitric acid, &c. Ferric thiocyanate also dissolved gold, but in this case it was supposed that the presence of dissolved oxygen was necessary. It is considered that the Stark process, in which thiocyanates are used, may be of value in the treatment of old tailings heaps.
