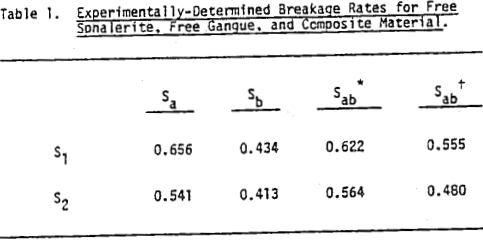
The metallurgical response of minerals during the flotation process are dependent upon two factors:
- The fragmentation of the minerals from each other during the grinding stage establishes the limits to process metallurgy
- The relative abundance of the different minerals in the ore sample dictates the complexity of the flowsheet design.
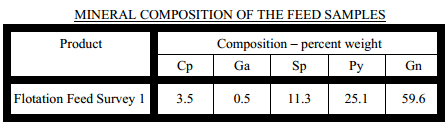
Here we discus the mineral composition and distribution of minerals by classes in the flotation feed stream. The flotation feed sample of this study was taken from a plant survey during which the plant was processing ore that contained relatively high levels of galena. This elevated galena content is reportedly indicative of ore that will be processed for the remainder of the mine life.
The dominant copper sulphide mineral present in the ore was chalcopyrite accounting for about 97% of the copper sulphide present in the feed and only minor occurrences of bornite. Of importance to metallurgical response, were the presence of tiny amounts of chalcocite and covellite. The presence of these copper sulphides could account for the pre-activation of sphalerite, resulting in significant contamination of the copper concentrate with sphalerite.
Standard mineral’s abbreviations:
- Cp-all copper sulphides including bornite, chalcocite and covellite
- Ga-galena
- Sp-sphalerite
- Py-pyrite- pyrrhotite
- Gn-non-sulphide gangue including hematite and magnetite.
The mineral fragmentation measurement provides important information regarding the primary grind required for a successful flotation separation to occur in the rougher-scavenger circuit. The requirement for regrinding can also be assessed from the same data set.
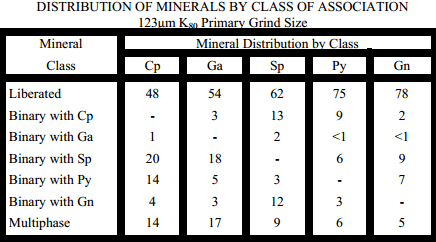
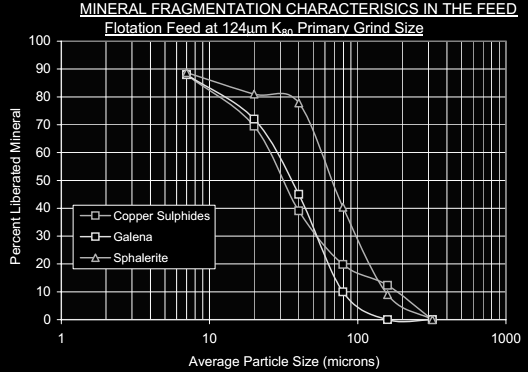
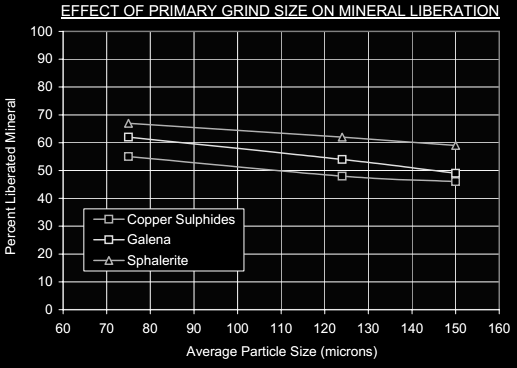
At a nominal 125µm P80 sizing almost half of the chalcopyrite is liberated. The remainder of the chalcopyrite is present as binary structures with sphalerite or pyrite or as more complex multiphase structures. These binary particles are relatively simple comprising on average 25% by weight chalcopyrite. The multiphase particles contain less than 10%t by weight chalcopyrite. Although liberation is adequate for copper rougher
flotation, the application of a small amount of regrinding power might improve liberation of the sphalerite from the copper sulphides. The multiphase particles are structurally much more complex, and therefore will probably not greatly benefit from regrinding as in this case the application of regrinding to improve sulphide-sulphide liberation levels could be futile resulting in simply producing smaller binary particles.
About half of the galena in the feed is liberated with the remainder distributed principally between galena-sphalerite binaries and as galena bearing multiphase structures. These binaries are structurally simple consisting of about 30% by weight galena. The multiphase particles comprise tiny adhesions or inclusions of galena on a much larger particle containing mostly non-sulphide gangue. The galena in these complex multiphase structures contain on average 1% by weight galena.
It is important to note that galena interlocking with chalcopyrite in the flotation feed stream is minimal. This should ensure an adequate level of chalcopyrite-galena selectivity. The selective rejection of galena from the copper flotation circuits, is physically feasible.
At the 125µm P80 primary grind size sphalerite is well liberated at about 60%. This level of liberation is, in our experience adequate to ensure successful flotation in the zinc rougher circuit.
- Flotation Process Development and Assessment
- Mineral Composition and Fragmentation
- Evaluating Copper Rougher-Scavenger Flotation Circuit Performance
- Measure and Evaluate Flotation Scavenger and Cleaner Tail Losses
- Effect of Regrinding
- Evaluating Copper Flotation Cleaner Circuit Grade/Recovery Results
 Random Sets and Integral Geometry in Comminution and Liberation of Minerals
Random Sets and Integral Geometry in Comminution and Liberation of Minerals
The study of random geometrical sets and their properties is a relatively obscure and difficult field in mathematics. In fact, very few research groups are active in this field, especially with a view to practical applications. To define broadly the themes covered in such studies, random geometrical sets are involved in a large number of fields, such as parking problems, dead leaves problems, metallurgical grain structures, etc, in other words, whenever it is desired to described in a non deterministic manner any geometrical feature.

dimension (this type of study is sometimes called stereology), or to assess the properties of remarkable bodies, such as convex solids. As mentioned previously, there are only a few researchers active in the field, among which Santalo in Argentina, who has written a standard book on the subject, Matheron and Serra in France, and Miles and Davy in Australia.
Applications to fracture of minerals
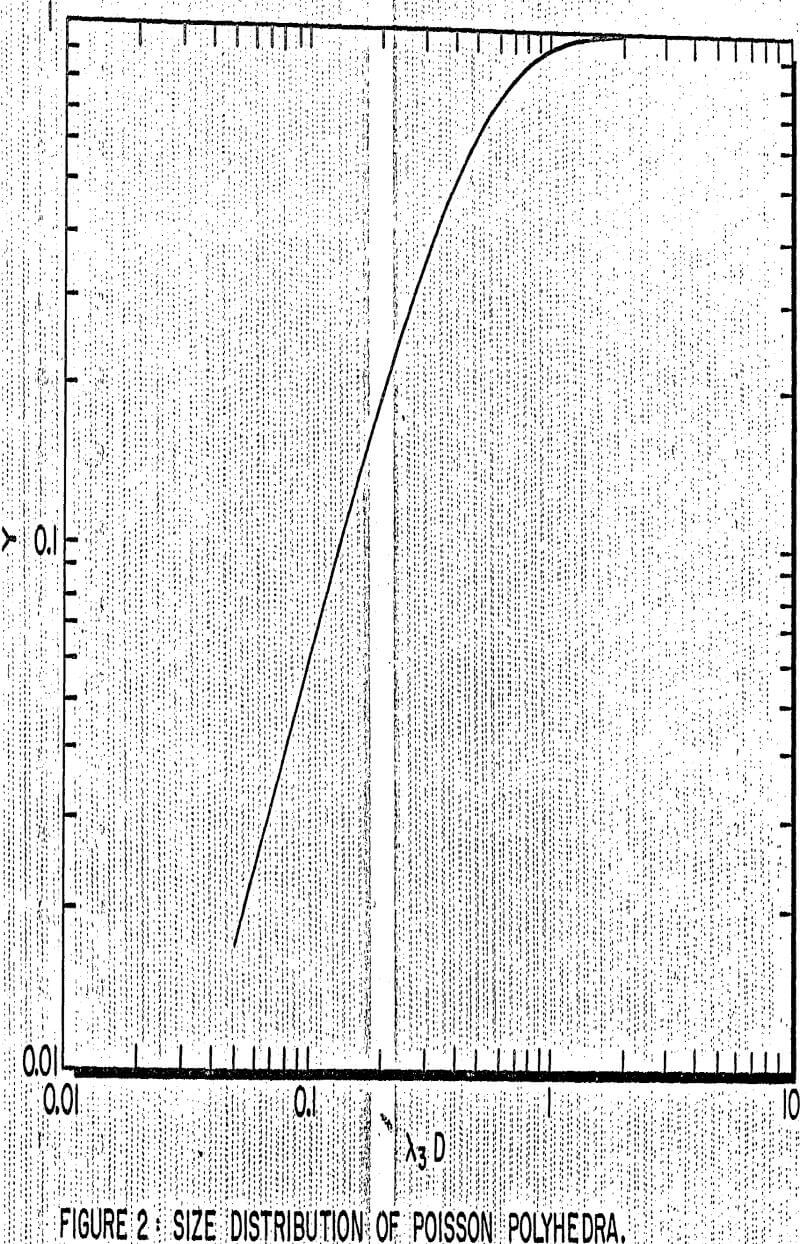
A typical example of the application of random sets and integral geometry to mineral processing problems is the prediction of fragment size distribution, after breakage, from first principles. The geometrical figures obtained in the plane are called Poisson polygons. They are in fact plane sections through Poisson polyhedra. Although the geometrical shape of the fragments is fairly complex, it is possible to obtain the mean volume by measure (i.e. by counting each polyhedron by its volume, as is done during particle sieve sizing), its variance, and particle specific surface area:
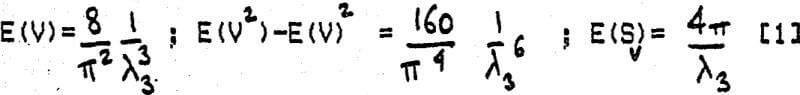
Another remarkable result is that polyhedra size distribution can be completely determined. The method of sizing must first of all be defined. A particle is measured at size D when a sphere of diameter D just fits inside it.
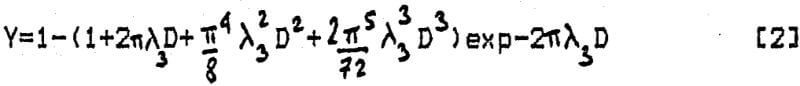
Applications to liberation prediction
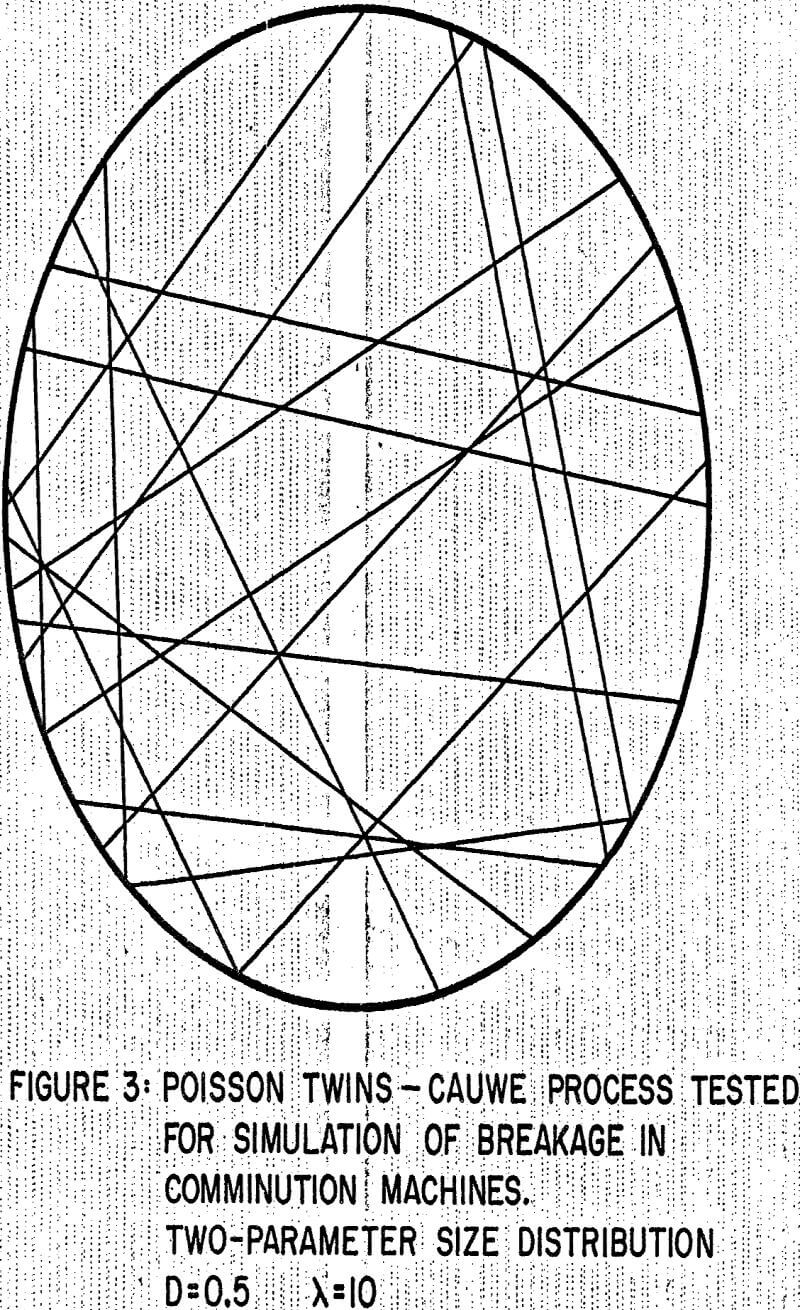
The application of random geometrical sets and integral geometry to studies of mineral or ore breakage is a little trivial, since very precise methods are available to measure particle sizes, and to model comminution machines, for example by using population balance models. The problem of liberation is much more interesting, since there is at present no general method for the determination of particle phase composition. Image analysis methods are generally thought to be the only alternative for the measurement of composite particles, and a review of the various methods that have been tested for the measurement and the reconstruction of the biased primary data.

Ore breakage modelling
In a similar manner, the description of ore breakage should consider that particles are produced by a stochastic geometrical process. It will be assumed to be stationary, isotropic, and producing particles that are quasi-convex in shape. This last limitation is strong in the mathematical sense, in that it will be used to apply the remarkable properties of convex bodies in integral geometry; it is felt that, on a practical point of view, it is not too strict since concave shapes would tend to produce mechanically weak particles that would break easily.
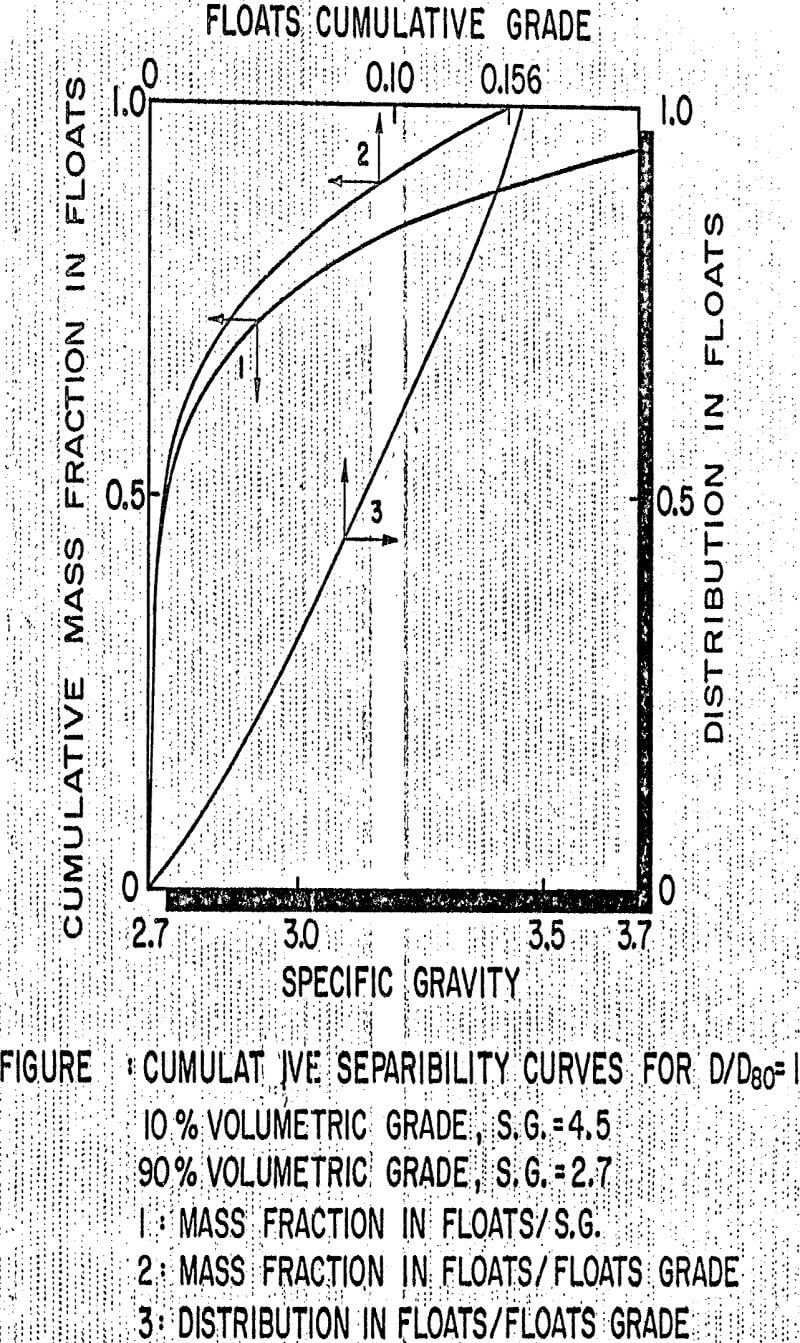
It is possible to quantify by image analysis techniques the various mathematical functions which are required in the model, thus making it amenable to calibration and testing, a feature not often encountered in previously developed liberation prediction models. It is felt that the model should be tested on various ores so that the main hypotheses that have been included, especially the one involving the lack of correlation between ore texture and breakage pattern, are validated. The model was demonstrated on a simple case, Poisson polyhedra ore texture and monodisperse spheres as fragment, and the potential of the method is clearly indicated by its ability to predict separability or washability curves. Correlations between existing washability curves and typical models a parameters should be tested, so that model calibration based on the results of heavy liquid separation, much cheaper than image analysis to carry out, could be attempted.

A Combined Size Reduction and Liberation Model of Grinding
Mineral beneficiation can be thought of as a two-step process. In the first step, mineral liberation occurs as particles are reduced in size, while selective concentration of the liberated species takes place in the second step. Unfortunately, comminution rarely results in complete mineral liberation and separation processes are seldom entirely selective.
Model Development
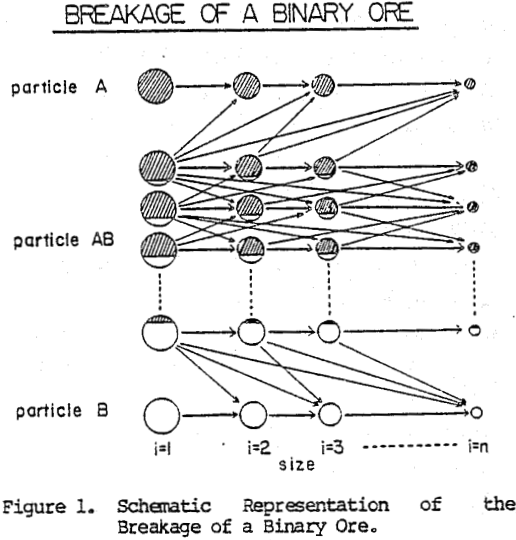
The model being presented here considers the breakage of a binary ore. While more complex systems could be modeled, a binary ore was used for mathematical simplicity.
Consider the breakage of a composite feed ore containing free A particles, free B particles, and composite AB particles. Free A particles can only be reduced in size; they cannot change to a different mineral content class. Likewise, free B particles can only be reduced in size. Composite AB particles, on the other hand, can produce free A particles, free B particles, and several classes of AB combinations. Therefore, a mass balance on material reporting to a given size class in a given mineral content class is composed of two components. Material can remain in the same mineral content class and simply be reduced in size, and material can be liberated from other mineral content classes into the class being considered.
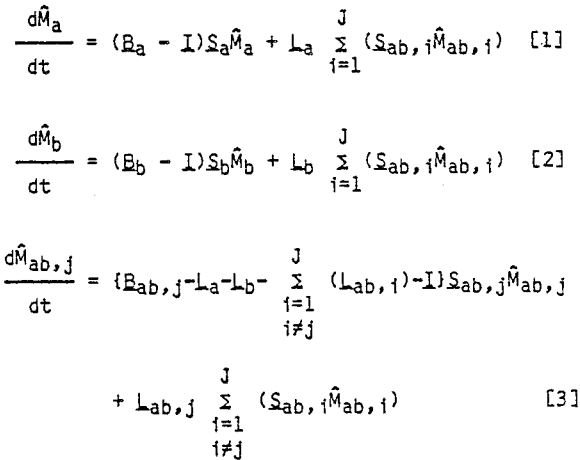
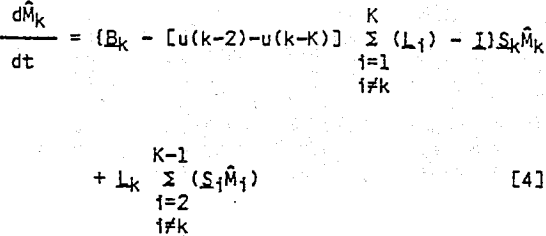
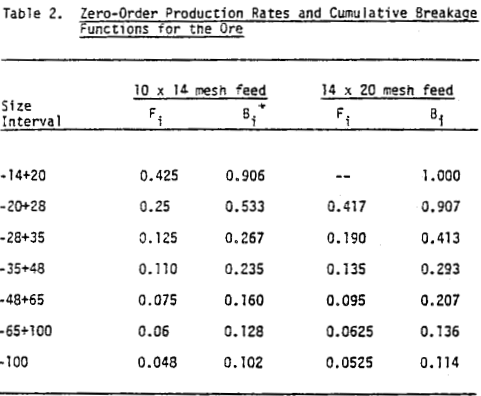
In order to estimate the breakage distribution and liberation distribution functions, it is necessary to apply the concept of zero-order fines production to the composite breakage-liberation model. Equations [1] – [3] are first written in cumulative form to give the following:
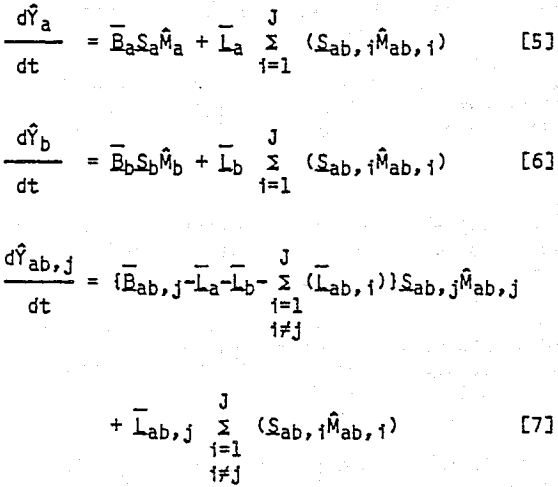

Experimental Procedure
The ore sample used in the present work was a coarse-grained sphalerite ore obtained from ASARCO’s Young Mine in Eastern Tennessee. The sample was taken from the coarse concentrate stream coming from the dense media separator. It contained approximately 12 percent sphalerite, and it very nearly approximated a binary mixture of limestone and sphalerite, making it ideally suited for the present work.
In order to obtain liberation data, polished particle mounts were made from the various size fractions produced during the batch grinding experiments. Representative portions of the various ore samples were first treated with ethanol to keep the particles separated in the mount. These samples were then mounted in a cold setting resin (EPOFIX Epoxy).
The liberation data used in the present work were obtained by an areal scanning technique on microscope images of polished particle mounts. Since each briquette contained particles of the same size fraction, the volume fraction of free particles was determined by simply counting the number present in the sample. This eliminated unnecessary bias due to orientation effects in the sample.
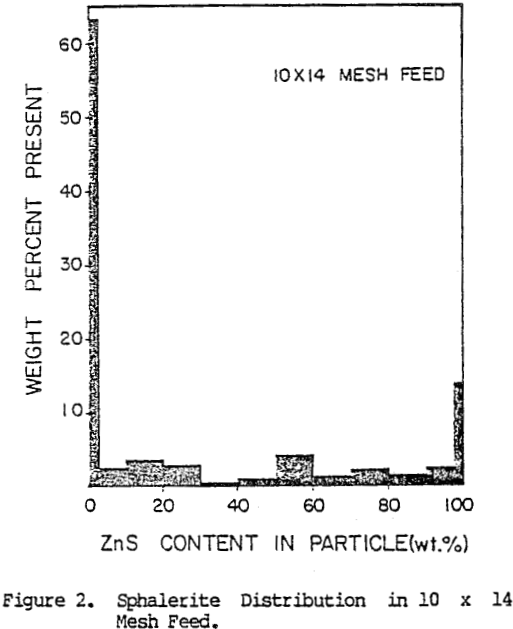
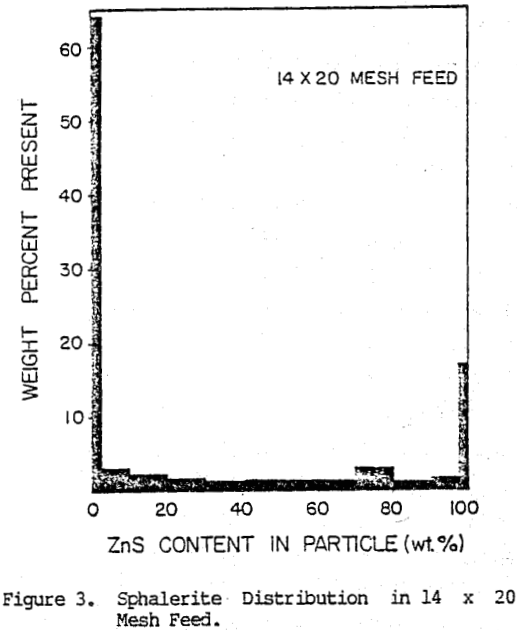
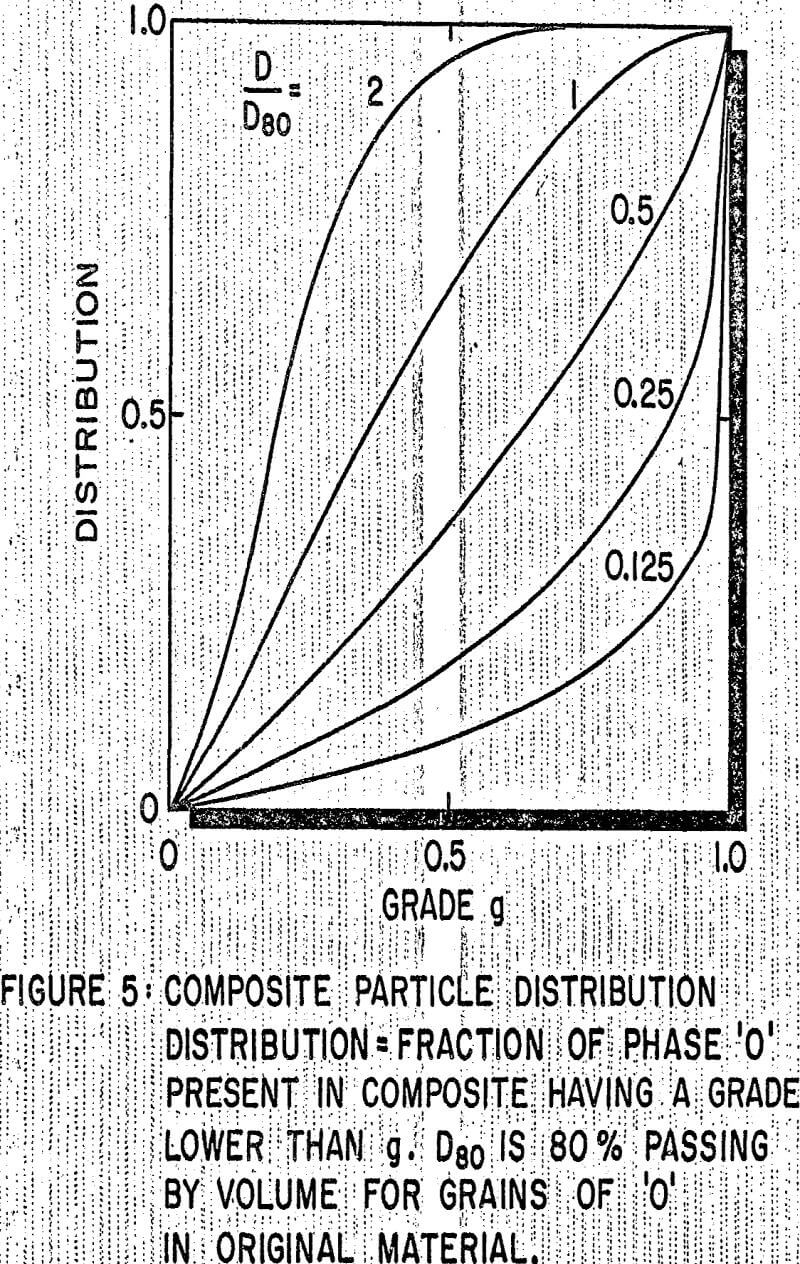
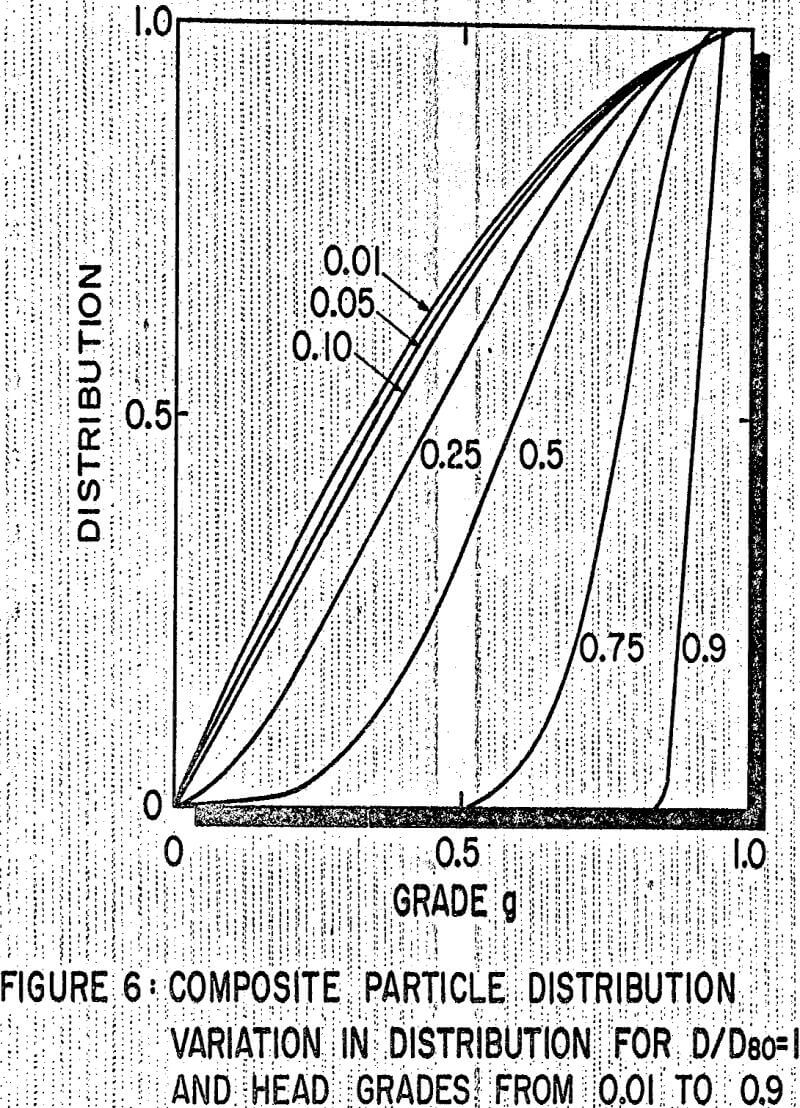
The image analysis characterization of the two monosized feeds tested to date is shown in Figures 2 and 3. The characterization is presented in the form of a histogram representing the weight percent of material present in the feed containing various amounts of sphalerite. Completely liberated particles are assumed to contain less than 2 percent sphalerite or greater than 98 percent sphalerite.
For the total ore free sphalerite, free gangue. and binary composite particles contained in the ore. In these plots, all composite (or locked) particles have been grouped in one class since at present, insufficient data have been collected to determine breakage rates for various classes of composite particles.