Modelling Solvent Extraction of Copper in Ammoniacal Systems

A mathematical modeling method was developed by the Bureau of Mines for the prediction of the principal equilibrium species in the solvent extraction of copper. The use of models for predicting the amount of metal extracted can reduce the amount of experimental work required to characterize a system for purposes such as optimization studies. Models were developed for the extraction of copper from ammoniacal sulfate and carbonate solutions with commercially available extractants commonly used by industry. Results from laboratory shakeout tests compared well with predictions of the equilibrium concentrations of copper and pH values. For example, the loading of copper onto the solvent was predicted for most cases within ±5 pct of the measured values, and the pH to within ±0.1 pH unit in sulfate systems and ±0.2 pH unit in carbonate systems. Both mechanistic and empirical extraction equations were developed from laboratory data for copper and ammonia. The empirical-based models were slightly more accurate than were the mechanistic-based models. Industrial-level concentrations of the aqueous and organic constituents were used in this work. Independent variables included copper concentration, ionic strength, and initial pH of the aqueous phase; extractants, diluents, and their concentration in the organic phase; and temperature.

The development of more selective extractants in recent years has greatly expanded the consideration of and the use of solvent extraction in metal recovery processes. However, in many cases, the full capability of the extractant is not known and a great deal of experimental work is required to produce the necessary data so that process evaluation and optimization studies can be made. Solvent extraction processes are conventionally designed by carrying out many laborious shakeout tests, producing data for McCabe-Thiele and other diagrams, for evaluation of performance at each set of operating conditions. An easy to use mathematical solvent extraction model that is applicable to practical systems, covers a wide range of conditions, and is accurate, would be very useful.

Chelating reagents of the hydroxyoxime type have been used commercially for years for the extraction of copper from acidic solutions. Several relatively successful attempts have been made at proposing extraction mechanisms and at predicting metal extraction with hydroxy-oximes from acidic solutions. For example, theoretical-based models three-dimensional plots, and an empirical approach (40, were developed for prediction of copper extraction from acidic solutions. In recent years, considerable interest has been shown in using hydroxyoximes and other extractants for extracting metals from ammoniacal solutions. Ammoniacal-based processes have been proposed for metal recovery from low-grade laterites, from manganese nodules, from scrap, from sulfides, and from waste catalysts. The subject of this report relates to the modeling of copper extraction from ammoniacal solutions.

Some progress has been made at establishing extraction mechanisms and at predicting metal extraction from ammoniacal solutions; however, most of the models reviewed were limited in some important respects. Two similar papers used statistical techniques to develop empirical equations for the solvent extraction of copper. The first paper, dealt with copper extraction from sulfuric acid and from ammoniacal sulfate solutions with mixtures of LIX 64N and SME 529 extractants. The second paper, dealt with extraction of copper and/or nickel with LIX 64N or SME 529 extractants from ammoniacal sulfate solutions.

Based upon information provided in these papers, it appears that industrial-level concentrations of components were used in both investigations; however, the pH range of the solutions was not given. Empirical equations were presented for the calculation of the percentage of copper extracted, but not for any other equilibrium quantity. The majority of the data that served as the basis for these empirical equations represented the case where the ratio of metal in the system was very high compared to the amount of extractant(s) present. Thus, the data corresponded primarily to conditions of maximum metal loading on the organic phase and relatively low extraction percentages from the aqueous phases. Several equations were developed to predict copper extraction. The lowest standard error for one of these equations was 1.66 pct for the Cu-NH3-SO4-(SME 529 and LIX 64N) system. The average error in the predicted percentage of copper extracted was 3.9 pct for the Cu-NH3-SO4- SME 529 system and 6.0 pct for the Cu- NH3-SO4-LIX 64N system.

Theoretical-based equations were presented that predicted the extent of hindrance of metal extraction (Cu, Co, and Ni) that was due to the formation of ammine complexes in the aqueous phase. However, the experimental work dealt only with extractant concentrations in the organic phase that were greatly in excess of the concentrations of metal ions present. Therefore, unlike most industrial situations of interest, the free extractant concentration remained relatively unchanged during extraction in this investigation. In another paper, a mechanism was proposed for the extraction of copper with Versatic 10; however, a model or algorithm to allow utilization of the mechanism was not presented. Additionally, the mechanism was developed from data that were obtained from tests conducted under idealized conditions of constant ionic strength (1.0 M ammonium nitrate solution) and at very moderate pH levels.

Another theoretical-based equation was developed that described metal extraction from ammoniacal solutions. This equation, which depended upon prior knowledge of certain equilibrium data, showed good agreement with some nickel data in an ammoniacal sulfate system. However, idealized conditions were employed in the tests from which the equation was developed: very low metal loading on the organic phase was used, only one concentration of nickel in the aqueous phase, and one concentration of extractant in the organic phase were investigated. Application of this equation to the extraction of copper was not described in the paper. However, a rigorous method for predicting copper and nickel extraction in an ammonium carbonate system was described in another paper. Unfortunately, the algorithm used for the predictions was only briefly outlined and the coefficients for the extraction expressions were not supplied. Industrial-level concentrations of components were used in this investigation, but only one level of extractant concentration was considered (40 vol pct LIX 64N). Results predicted with this method were compared with experimental results and average errors of 10 to 15 pct were obtained.

Since a need was recognized for an improved solvent extraction model for ammoniacal systems, fundamental research into the equilibrium modeling of the solvent extraction of metals was pursued by the Bureau. As the first part of this research, the extraction of copper from ammoniacal solutions with commonly used extractants, LIX 64N4 and P5100, was investigated. The primary goal of this research was to develop a mathemetical model that could predict the equilibrium loading of copper on the solvent to within 5 pct of the actual concentrations. Additional goals of this effort were to develop a model that required only limited initial condition parameters and could accurately predict equilibrium values in practical situations, i.e., relatively high metal loading from high-ionic strength solutions such as might be obtained in industrial leaching processes.

This report describes a systematic laboratory study of the extraction of copper from ammoniacal sulfate and carbonate solutions with LIX 64N and P5100 extractants. Models were developed using both empirical- and theoretical-based extraction equations. The methodology for developing the data and the corresponding mathematical models are completely described so that application of this methodology can be made to other solvent extraction systems. The effects on the models of many variables were investigated, such as the effect of different extractant concentrations and different concentrations of aqueous phase components. Extraction equations were developed for two different extractants, kerosene diluents, and temperatures.

Reagents and Solutions

Two ammoniacal copper systems were investigated in the laboratory work, copper-ammonia-sulfate (Cu-NH3-SO4) and copper-ammonia-carbonate (Cu-NH3-CO3). The solutions were prepared with reagent-grade chemicals and de-ionized distilled water and were enclosed in plastic bottles for storage when not in use. The concentrations of the constituents in the feed liquors were chosen based upon available industrial data and the physical constraints of the systems (table 1). Because of solubility constraints, copper carbonate solutions required higher pH levels than did copper sulfate solutions. Solution pH levels for the various tests

were adjusted to the desired level by sparging ammonia gas into the solution or by the addition of ammonium hydroxide. Because of the volatility of the aqueous solution components, particular care was taken to keep container opening at a minimum, especially when test conditions called for elevated temperatures. In addition, each feed liquor was sampled and analyzed to determine the concentration of the constituents at the time of each test.

Two commonly used commercial extractants were used in this study, LIX 64N and P5100. The extractants were used as-received without purification, to simulate industrial practice. Solvents were mixed as required to nominal concentrations of 1, 10, and 25 vol pct extractant. Dilutions were made with either Kermac 47 OB or Solvesso 100 kerosenes. As recommended by Ritcey, the solvents were conditioned before use in the tests. This simulated the use of recycled solvent and helped remove any aqueous-soluble impurities from the solvents. The conditioning consisted of the following steps: (1) the solvent was loaded to near its maximum loading capacity with a Cu-NH3-SO4 solution pH -8. 5, (2) the loaded solvent was stripped with a 160-g/L H2SO4 solution, and (3) the stripped solvent was washed with distilled water.

All of these steps were conducted at an organic (O) to aqueous (A) ratio of 1 (O/A = 1). It was necessary to strip the P5100 solvents twice in order to bring the residual copper concentration to low levels. The conditioned solvents were then analyzed to determine the extent of impurities remaining. Usually at this stage, the solvents contained very low copper concentrations (several parts per million) and only minute traces of other impurities.

Following dilution and conditioning of the solvents, the effective concentration of extractant within each solvent was determined through an ultimate-loading capacity determination with copper. This type of determination is often used in commercial copper solvent extraction plants. The ultimate-loading capacity was determined by repeatedly contacting an aliquot of solvent with fresh aliquots of a Cu-NH3-SO4 solution at pH -7.5 until the raffinate analyses showed no further copper extraction. To avoid phase separation problems during the loading tests, the 10- and 25-vol pct solvents were diluted with an appropriate kerosene to a concentration of approximately 1 vol pct. After the loading tests the solvents were analyzed for copper; the extractant concentrations were calculated from that result and the assumption that 1 mol of copper combined with 2 mols of extractant. Dilution factors were also taken into account in calculating the extractant concentration. The loading determinations were conducted with solutions containing about 2.5 g/L Cu, 58 g/L SO4, and 20 g/L NH4 (total) and were at O/A = 1 and 40° C.

Tests and Procedures

Shakeout and loading curve tests were conducted using only conditioned solvents. The concentration ranges of metals and anions of the aqueous solutions were derived from industrial data and were shown in table 1. The tests were arranged so that copper concentrations in the feed liquors ranged from about 25 pct up to 120 pct of the theoretical maximum loading capacity of the solvent being contacted. Thus, the data and resultant models bracketed the range of solvent loading that is most often used by industry (25 pct up to essentially 100 pct of maximum capacity). In order to reduce the number of variables to be considered, the O-A ratio was held constant at 1 in all tests. Thus, the models in their present form are limited to situations where an O-A ratio of 1 is used. However, many industrial operations using solvent extraction for metal recovery operate at O-A ratios around 1.

Shakeout Tests

Shakeout tests were performed in separatory funnels that were shaken mechanically in a thermostatically controlled apparatus. Aliquots of feed liquor and conditioned solvent were equilibrated for a period of 30 min, which was found to be more than sufficient to reach chemical and thermal equilibrium. During the shakeout tests, the separatory funnels were periodically vented to maintain essentially atmospheric pressure. A small loss of ammonia and possibly some carbon dioxide from the carbonate systems was experienced, but this was inevitable. The amount of volatiles lost was considered to be insignificant compared with the amounts present in the solutions. After the shakeout contact, the phases were separated. The solvent phase was filtered through phase separation paper (Whatman-1 PS) to remove any traces of aqueous entrainment. The raffinate was filtered (S and S-Black Ribbon) to aid in removal of any organic entrainment. The phases were then sampled for analysis and further testing. The raffinates were brought back to the appropriate temperature (25° or 40° C) for measurement of the final pH.

The feed liquors and raffinates were analyzed for Cu, SO4 or CO2T, NH4T, and in the sulfate system for NH3 (total).

The CO2T corresponded to the equivalent total CO2 in solution ([CO2] + [CO3²-] + [HCO3-] + [NH2COO-] + etc). The NH4T corresponded to the equivalent total NH4 in solution ([NH3] + [NH4] + + x[Cu(NH3)x²+]). In addition, the feed liquor and the raffinate pH’s were measured and spectrographic analyses were made to determine the average copper-ammonia coordination numbers (described later in this report). It was possible to determine the NH3 (total) concentration in the aqueous solutions of the sulfate system through titration of the solutions with a standardized H2SO4 solution (0.14N). The NH3 (total) value, coupled with the spectroscopically determined average coordination number and the measured copper concentration, allowed calculation of the free NH3 concentration of the aqueous solutions.

In the carbonate system, titration methods could not accurately differentiate between neutralization of NH3 and CO3²- and related compounds. Therefore, it was not possible to determine the free NH3 concentration in the carbonate solutions used in this investigation. An aliquot of the loaded solvent was stripped with a 150 g/L H2SO4 solution. The resulting strip solution was analyzed for NH4+ ion, and based upon that value, the NH3 loading on the solvent was calculated. The remaining portion of the loaded solvent was analyzed for copper.

Copper was analyzed in the solvent by wet-ashing the solvent, dissolving the wet ash in an acidic solution, and final analysis for copper either through atomic absorption (for levels <0.1 g/L) or titration with ethylenediamine tetracetic acid (EDTA). Aqueous copper analyses were made either directly through atomic absorption or EDTA titration depending on the copper concentration. Total NH4 concentrations were determined by a modified Kjeldahl method and sulfate by a gravimetric BaSO4 method. A Leco carbon-sulfur analyzer was used to analyze for CO2 by igniting aliquots of aqueous samples and reading the resulting infrared spectrum. In all cases, analytically determined equilibrium copper concentrations were checked by determining material balances, and analyses of liquor components (e.g., Cu, SO4, and NH4T) were checked with an ionic balance.

The models included equations for material balances and the calculations could not be expected to converge well if the analytical results did not balance well. In the majority of cases the errors in material balances were less than 5 pct. However, in the cases where the errors were greater than 5 pct the analytical data were adjusted to allow closure of the balances. These data and unadjusted data were then used both to develop the extraction equations and to test the resultant complete models.

The shakeout tests were designed to cover a wide range of practical conditions. Feed liquors were used that contained nominal copper concentrations corresponding to 50, 75, 100, and 120 pct of the maximum copper loading capacity of the particular solvent used in the tests. In several tests, ranges as low as 25 pct were used. For each range, conditions corresponding to medium and high anion concentrations were investigated at pH levels of about 7.5, 8.5, and 9.5. Therefore, each shakeout series investigated the effects on copper extraction of the following variables: aqueous copper concentration, total ammonia concentration, anion concentration, and initial pH. In addition, most shakeout series were conducted at several extractant concentrations (1, 10, and/or 25 vol pct).

Loading Curve Tests

Loading curve tests were performed using many of the same general conditions and procedures as in the shakeout tests. A loading curve was developed through a series of individual shakeout tests. An attempt was made in each individual series of tests to hold all parameters constant except for the copper concentration of the feed liquor. The parameters for each individual series were arbitrarily chosen based upon available industrial data (i.e., SO4 concentration, NH4T concentration, extractant concentration, and pH). The tests were conducted so that the pH of the raffinates were all about 8.8±0.1 pH unit. Any raffinate outside of this range necessitated a repeat test with readjustment of the feed liquor pH.

Some parameters were varied, such as SO4 and NH4T concentrations, from one loading curve series to another. This produced a family of curves demonstrating the. effect those parameters had on copper extraction. The loading curve series was generally developed from data where the feed liquors contained nominal copper concentrations corresponding to 25, 50, 70, 90, 100, and 120 or 140 pct of the maximum copper loading capacity of the particular solvent used.

Precision

Duplicate, and in some cases, triplicate, tests were made on numerous shake-out tests and analyses. The estimated standard, deviation for replicate tests was about 2 pct for Cu and SO4 and 17 pct for NH4T. The repeatability of pH measurements was estimated to average ±0.05 pH unit. The accuracy of the pH measurements was estimated to average ±0.02 pH unit. The analytical laboratory accuracy and repeatability were found to be equal to or better than other measured parameters used in the model development.

Mathematical Basis for Model

Chemical Reactions

The extraction of divalent cations from ammoniacal solutions by hydroxyoximes has often been represented simply by the reaction equation

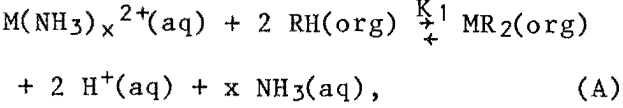
where M = divalent metal, such as copper,
RH = extractant in the solvent phase,
x = average coordination number of the metal ion,
and K1 = equilibrium constant for the reaction.

This simplified reaction equation ignores the possibilities of dimerization or higher polymerization of the extractant and complexation of the extractant complex by additional extractant molecules or by aqueous phase ligands. However, it does show the possible influence that hydrogen ions and free ammonia have on the extraction equilibrium. Since this study was carried out under basic conditions, the hydrogen ion liberated from the extractant is immediately reacted with ammonia to form ammonium ions, and can than be essentially ignored as far as reaction A is concerned. However, the concentration of free ammonia can have a significant effect on the extraction of metals.

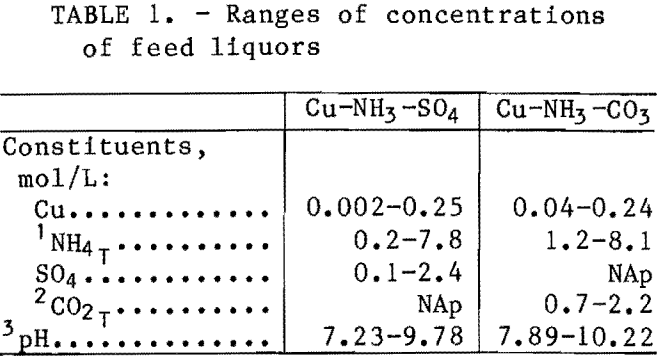
The loading behavior of the Cu-NH3-SO4- LIX 64N system was investigated in the initial studies. Shakeout test data are shown in figure 1, along with the ideal- loading curve and the theoretical maximum loading capacity of the solvent. The ideal-loading curve represents the case where essentially all of the copper that enters the system is extracted by the solvent until the solvent’s maximum loading capacity is reached, at which point the amount of copper extracted remains constant.

Analysis of these and other data indicated that the ideal-loading curve was followed until the solvent was about 80 pct loaded; the extraction data then deviated from the ideal curve. The extent to which the data deviated from the ideal-loading curve and the theoretical maximum loading capacity was a function of the conditions, such as the concentration of (NH4)2SO4, the pH of the

raffinate, etc. The extraction of copper seemed to be suppressed by the free ammonia concentration in the raffinate. The free ammonia concentration of these solutions was generally higher in the solutions with higher (NH4)2SO4 concentrations and higher pH. These and other data indicated that complex interactions in the aqueous phase were affecting the extraction of copper. Given this background, it was felt that a chemical-equilibrium approach would likely result in the most accurate predictive model for the Cu-NH3-SO4 and Cu-NH3-CO3 systems.

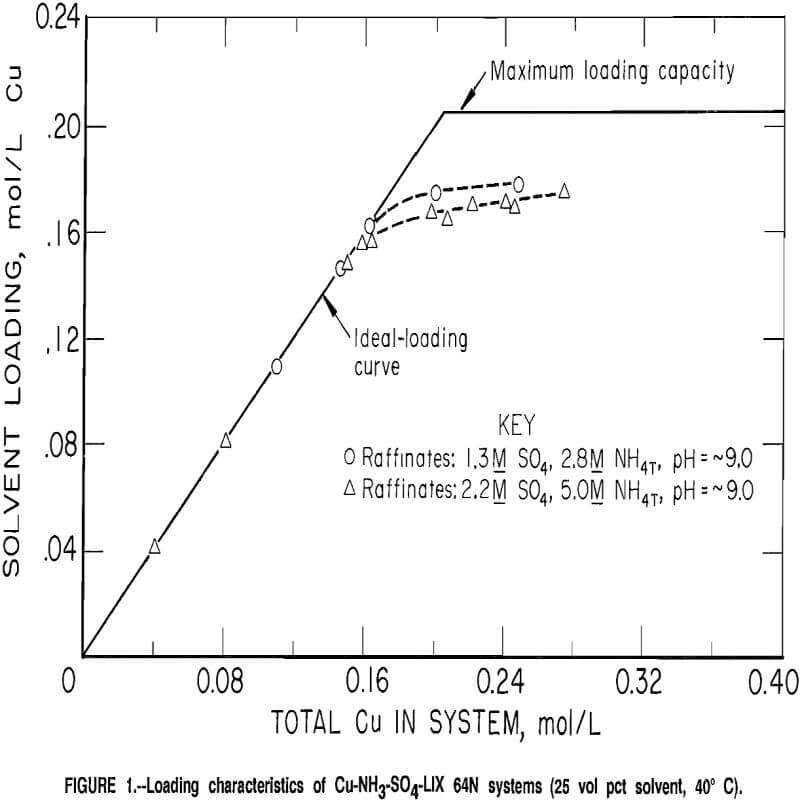
The aqueous chemistry in the ammonium sulfate solutions can be represented by the following equilibria:

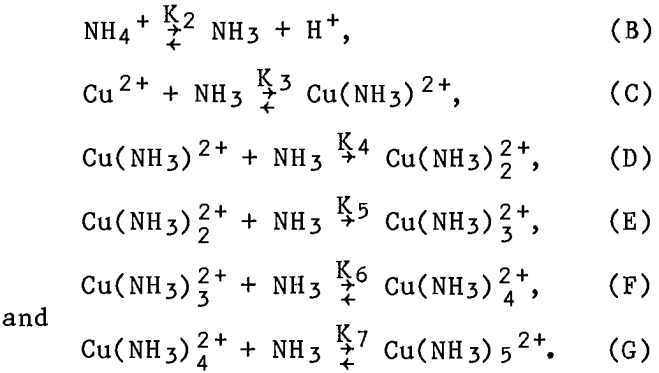
When considering ammonium carbonate solutions, additional equilibria must be considered:

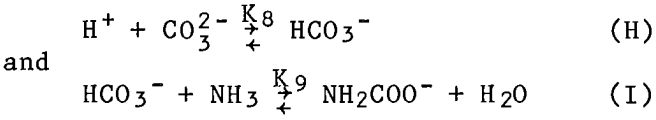
The amount of free carbon dioxide dissolved in aqueous carbonate solutions has been estimated to be about 0.6 pct at pH 8.5, and decreases at higher pH. Dissolved carbon dioxide has been ignored in this work. Ignored also were complications caused by the formation of Cu-NH3-Y complexes, where Y may be HCO3-, NH2COO-, or similar ligands. Some of the data suggested that this type of complex formation may have taken place, but specific complexes could not be identified.

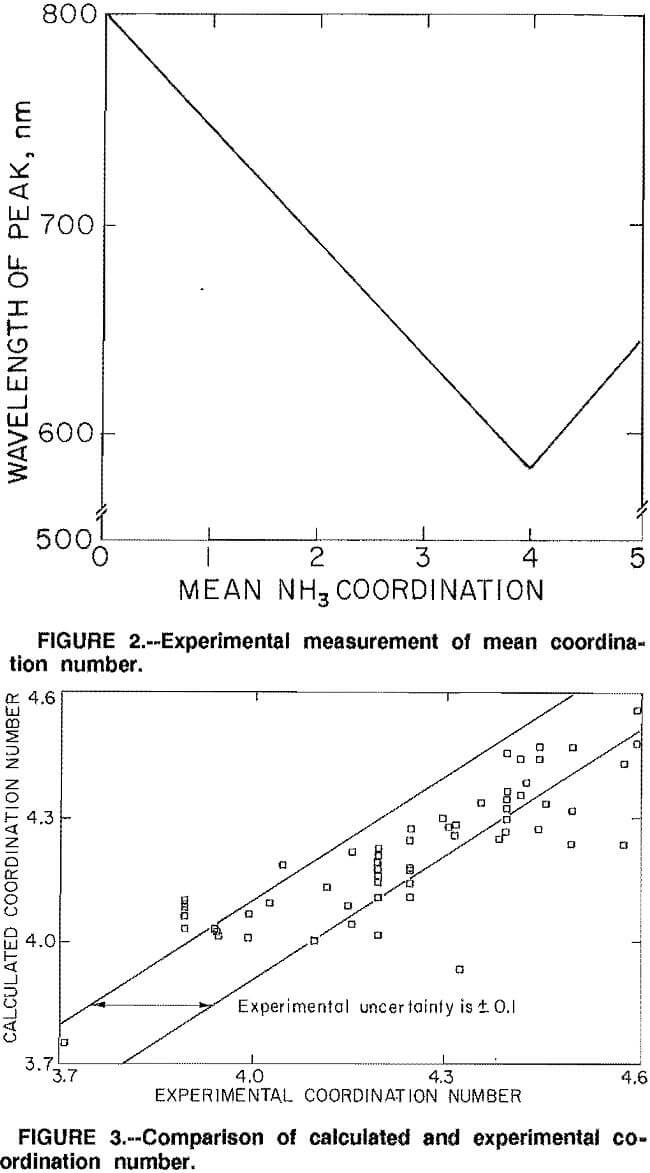
A complicating reaction that takes place between the solvent phase and the aqueous phase is the extraction of ammonia. The following reaction has been proposed (18):

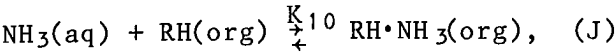
but other reactions might also occur. A secondary objective of this research has been to determine the mechanism of ammonia extraction.

Equilibrium Constants and Expressions

Numerical equilibrium constants or expressions are necessary before solution of the equations is possible. In several cases, literature values were adequate, but in some cases it was necessary to develop empirical expressions to describe equilibria in the high-ionic-strength solutions of this investigation.

An empirical equation for the effective equilibrium constant was developed for the dissociation of ammonium ion in ammonium sulfate solutions at 20° C. The equation was developed from data obtained from solutions with ionic strengths ranging from 0.5 to 6.0. The equation was extended to other temperatures by using the van’t Hoff equation with enthalpy values from reference 19. The resulting equation, with concentrations expressed in moles per liter, is

-log(K2) = 0.1774 + 2,727/(273 + t) + 0.2985 (µI)½,…………………………………………(1)

where log = logarithm to base 10,
t = temperature, °C,
and µI = the ionic strength.

Literature values were used for the copper-ammine complex instability constants. First, a uniform adjustment for temperature (t) and ionic strength (µI) was calculated,

adj = 0.10µI – 1,201(1/298 – 1/(273 + t)),……………………………………………………….(2)

where t = temperature, °C.

Then, the adjustment (adj) was used to calculate the logarithms of the equilibrium constants;

log(K3) 4.04 + adj,……………………………………………..(3)

log(K4) 3.42 + adj,……………………………………………..(4)

log(K5) 2.79 + adj,……………………………………………..(5)

log(K6) 2.01 + adj,………………………………………………(6)

and

log(K7) = -0.75 + adj,…………………………………………..(7)

Although these values were measured in nitrate solutions, they were applied in this research to both the sulfate and the carbonate systems. The mean coordination numbers were calculated from these constants and their equilibrium equations, and compared with experimentally measured coordination numbers. Experimentally, the coordination number was determined from the wavelength of the spectrophotometric absorption peak using the empirical relationship plotted in figure 2. The comparison, shown in figure 3, is fairly good.

The carbonate-bicarbonate equilibrium was investigated as part of this research, and the results indicated small but nonlinear effects of the ionic strength and the carbonate-bicarbonate ratio on the effective equilibrium constant. A mathematical equation was not fitted to these data, but weighted average values were selected and an empirical equation was developed to adjust the equilibrium constant for temperature effects:

1n(K8) = 17.69 + 1,501/t………………………………………………………….(8)

where 1n = the logarithm to base e
and t = temperature, K.

An equation was obtained from the literature (20) for the equilibrium constant for carbonate formation at different temperatures:

1n(Kg) = -8.6 + 2,900/t,……………………………………………………………..(9)

where t = temperature, K.

Extraction Equations

A major objective of this research was to develop a mathematical model of the extraction of copper from ammoniacal solutions that could be applied to solvent extraction systems over a broad range of conditions. Either of the two general classes of model would be acceptable: empirical or mechanistic. A combined model, where some parts were mechanistic and some were empirical, would also be acceptable.

The empirical extraction model ignores the actual reaction mechanism, and simply finds an equation that fits the experimental data. Usually the form of the equation selected is one that is mathematically tractable. The advantage of the empirical extraction model is that useful results can be obtained with relatively little effort. The disadvantages of the empirical extraction model are that the model reveals nothing of the reaction mechanism and that the resultant equation is usually applicable only to a limited range of conditions.

The mechanistic extraction model assumes a set of reaction equations that is supposed to describe the actual reaction mechanism. The set of mass-action equilibrium equations appropriate to the reaction equations can be solved simultaneously with the appropriate mass balance equations to determine the equilibrium conditions from a limited set of starting conditions. If the correct reaction mechanism is selected, the set of mechanistic equations should describe the extraction over the full range of possible conditions. However, the complete and correct reaction mechanism is not known. Sometimes simplifying assumptions can be applied successfully, but often they cannot. The procedure then becomes a matter of trial-and-error applied to intuition about the chemistry of the extraction.

Empirical Extraction Equations

The empirical extraction equation for copper relates the concentration of the extracted copper in the solvent to the concentration of the extractant and the concentrations of the components in the raffinate. The form of the equation selected is that of a mass-action equilibrium expression, but with nonintegral exponents, e.g., [Cu(org)] = a[Cu(aq)]b [NH3(aq)]c. The equation is a series of products, so the logarithm is a series of sums for which the coefficients can be estimated by multiple linear regression analysis.

The calculations were made using commercially available statistical programs on a microcomputer. The list of independent variables included the concentrations of the aqueous copper, the ammonium ion, the free ammonia, the ionic strength in the aqueous phase, the total extractant, and an estimate of the free extractant in the solvent. The regression program produces an estimate of the probability for each coefficient that the coefficient is equal to zero. If that probability for any independent variable were greater than 0.05, that variable was removed (In a backwards stepwise procedure) from the set of independent variables and the regression was recalculated. As might be expected, different data sets often have very different equations. In some cases several different equations seem to fit the same data set almost equally well. The intermediate results obtained with the individual sets of trial extraction equations are given in appendix A.

The most accurate empirical-based equations for copper and ammonia extraction that were developed in this research are

where A0 to A5 and B0 to B5 are empirical coefficients. Values for the coefficients for the systems investigated are listed in appendix A (table A-3).

Mechanistic Extraction Equations

When all the chemical reaction mechanisms are known, with their reaction constants, the extraction can be calculated within experimental error for all experimental conditions. The procedure followed to find a suitable mechanistic extraction model was to use first the most obvious mechanisms, and then add other reactions until the model fit the data within experimental error. A non-linear least squares technique was used to evaluate reaction parameters. The procedure used was to minimize the weighted sum of the copper error squared plus the extracted ammonia error squared, with the weights proportional to the reciprocals of the respective variances.

The most obvious extraction reactions are

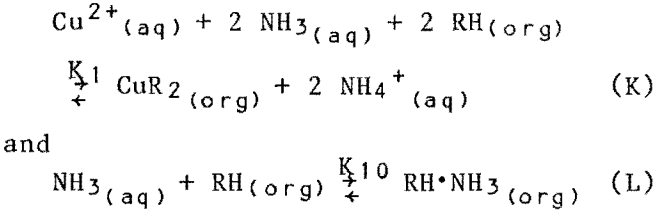
where CuR2 = copper-extractant complex in solvent phase, mol/L.

The concentrations of the ammonia species and the solvent copper were analyzed, and the free aqueous copper was estimated from the system of reactions:

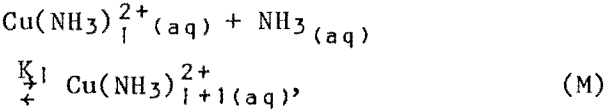
with i ranging from 0 to 4. Equilibrium constants for these reactions are available in the literature. The concentration of free RH was then estimated from the material balance for the extractant:

[RHT] = [RH] + 2[CuR2] + [RH · NH3]……………………………………………………..(12)

The following additional reactions were also considered reasonable, and were tested in various combinations:

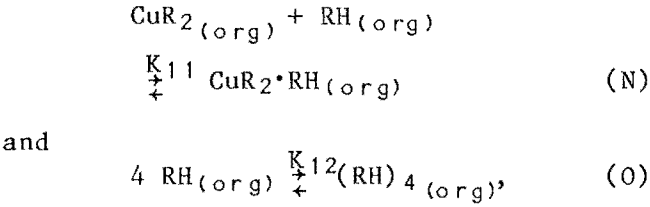
where CUR2·RH and (RH)4 represented extra complexation and polymerization of extractant in the solvent phase. These reactions (K-L, N-O) fit the data well and were used in the mechanistic-based models. The intermediate results obtained with the individual sets of trial extraction equations are given in appendix B. Values for the equilibrium constants are listed in appendix B (table B-1).

The equations for the extraction of copper and ammonia (empirical and mechanistic) were developed from data in the sulfate system. Models containing these equations were applied to data from both the sulfate and carbonate systems.

Supplemental Equations

A model based upon the preceding relationships must deal primarily with equilibrium values, which in practical applications usually are not available. A reasonable approach for solving such a model involves the simultaneous solution of all the pertinent equations. A sub-routine (ZSPOW) from the IMSL, Inc., library was selected to solve these nonlinear systems. However, additional equations were necessary to balance the number of unknowns in the sulfate and carbonate systems.

Sulfate System

The set of additional equations for the Cu-NH3-SO4 system (empirical-based model) included the following equations.

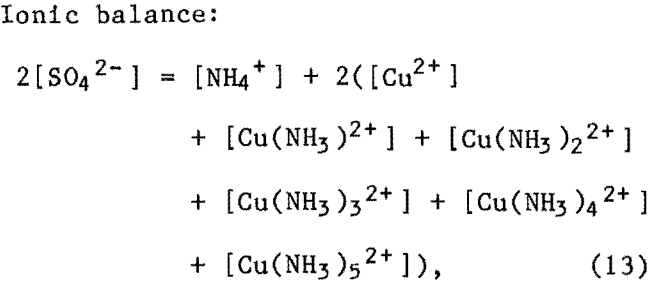
where [OH-] and [H+] were not included because of their low concentrations.

Total ammonia balance:

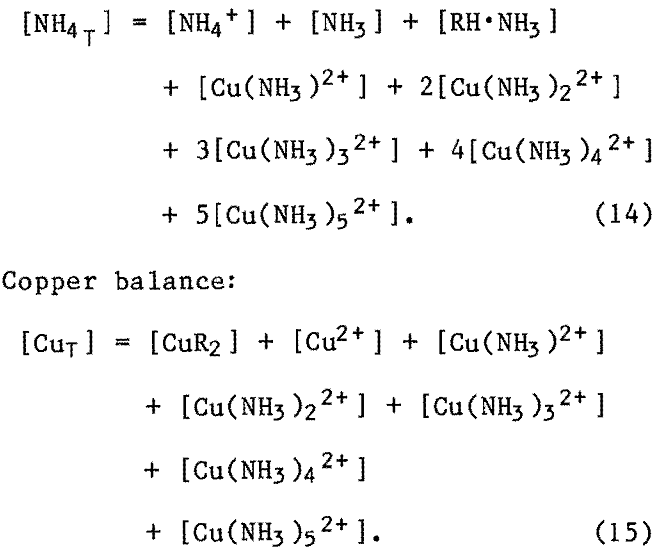
Extractant balance:

[RHT] = 2[CuR2] + [RH·NH3] + [RH]…………………………………………..(16)

The mechanistic-based model used the same supplemental equations except it required one additional term in the copper balance, [CuR2·RH], and two additional terms in the extractant balance, 4[(RH)4] and 3[CuR2·RH].

Carbonate System

In the carbonate system, some modifications to the balances of the sulfate system were necessary to reflect the different chemistry involved. The ionic balance was modified by replacing the 2[SO4²-] term with the terms 2[CO3²-] , [HCO3-] , and [NH2COO-]. The total ammonia balance was modified by adding an [NH2COO-] term. A supplemental equation was needed in the carbonate system to balance the number of unknowns.

Total carbon dioxide balance:

[CO2T] = [CO3²-] + [HCO3-] + [NH2COO-]……………………………………………..(17)

Model Algorithms

Solving nonlinear equations or nonlinear optimization problems is something of an art; convergence is often dependent upon the subroutine used and the initial parameter estimates. The ZSPOW subroutine selected for this purpose uses a variation of Newton’s method, which uses a finite difference approximation to the Jacobian matrix. The method of solution used in the ZSPOW subroutine is a local method; therefore, a successful solution depends on a good starting point. An initial estimate section was developed for the model, which provided estimated values for the required equilibrium variables from limited-initial-parameter inputs. Details of the initial estimate and other sections of the algorithm are given in the appendix.

Flow Charts

A composite flow chart for the sulfate and carbonate computational models is shown in figure 4. The information shown in this figure pertains to the models that used the empirical-based copper and ammonia extraction equations. However, very similar models were used with the mechanistic-based extraction equations.

Sulfate Model

As previously stated, the initial estimates section provided estimated values for the required equilibrium variables from limited-initial-parameter inputs. The required inputs to the computational models included the aforementioned

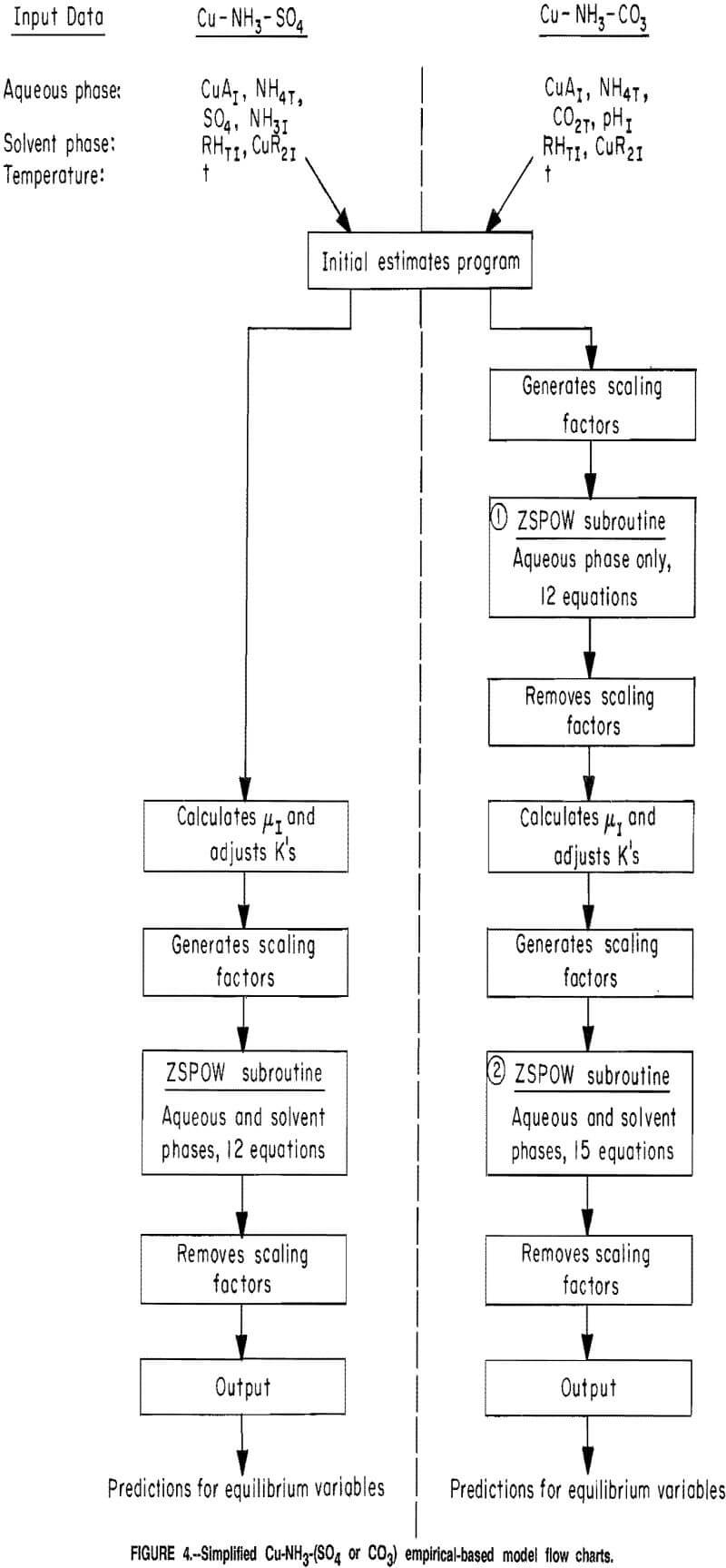
initial parameters, the temperature of the system, and the coefficients for the extraction equations. In the sulfate system, the ionic strength of the raffinate was calculated based upon results from the initial estimates section. The aqueous phase equilibrium constants were then adjusted taking into account the ionic strength and the temperature of the system. Scaling factors for the variables were used so that the convergence criteria of the ZSPOW subroutine would function properly. The values for the scaling factors were based upon the estimates of the variables that were generated in the initial estimates section. The scaled variables from the initial estimates section, adjusted equilibrium constants, and the scaling factors were transferred to the ZSPOW subroutine for solution of the equation-set. The following were used in the equation-set to describe the sulfate solvent extraction system: reactions B-G and equations 10-11, 13-16. Results from the subroutine were adjusted (scaling factors removed) and then printed.

Carbonate Model

The model for the carbonate system was very similar to the sulfate model, and only the major differences will be discussed in this report. Based solely on initial parameters it was difficult to accurately estimate the ionic strength of the raffinate. This was caused by the complexity of the possible anion reactions producing CO3²-, HCO3-, and NH2COO-. Therefore, an additional step was necessary to estimate the concentration of the various species present in the aqueous phase. The equations that pertained only to the aqueous phase were solved simultaneously (first ZSPOW subroutine call) to provide refined estimates for the aqueous phase variables. The reactions and equations used in this section were B-I, 15, 17, and 13 and 14 after conversion to the carbonate system.

Literature values were used for the equilibrium constants in this iteration. The results from this first iteration were used to calculate the ionic strength of the raffinate. As in the model for the sulfate system, the ionic strength was then used to adjust the values of the equilibrium constants that were subsequently used for the solution of the entire system (second ZSPOW subroutine call). The following reactions and equations were used to describe the entire carbonate solvent extraction system: B-I, 10-11, 15-17, and 13 and 14 after conversion to the carbonate system. Because of the lack of literature data for concentrated carbonate solutions, the same equations that were used in the sulfate system for adjustment of the equilibrium constants for Cu-NH3 coordination and the dissociation of NH4+ were used in the carbonate system.

Results and Discussion

As explained in this report, four related but somewhat different mathematical models were developed to predict copper extraction from ammoniacal solutions. Models were developed for the two principal ammoniacal systems that have been used in the hydrometallurgical processing of ores, ammoniacal sulfate and ammoniacal carbonate. Models for these systems used either empirical- or mechanistic- based equations to describe copper and ammonia extraction. The majority of results presented in this report correspond to the extraction of copper at 40° C with solvents containing LIX 64N and Kermac 470B; however, some investigations were made with P5100 extractant, Solvesso 100 diluent, and at 25° C. Although models that used empirical-based equations to describe copper and ammonia extraction were emphasized in this work, some results from models that used mechanistic- based equations were also included.

For a model to be truly successful it must be able to converge on reasonable results the majority of the time. In this work, two criteria had to be fulfilled before the model was considered to have converged with a given data set. The first criterion was a message from the subroutine that convergence was reached (IER=0). The second criterion was that the composite of the equation residuals yielded a low value (FNORM <0.1). Details of the convergence criteria are given in appendix D.

LIX 64N Extractant

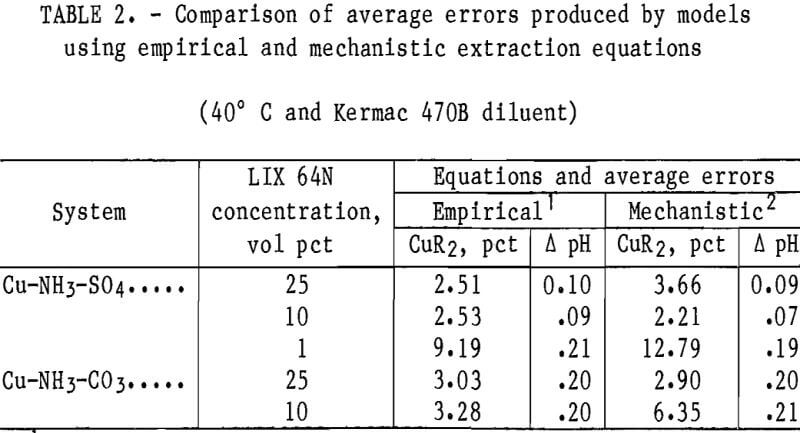
Results from operation of the appropriate models with essentially all of the LIX 64N data sets at 40° C and with Kermac 470B are shown in table 2. In most cases, the average errors in the prediction of copper loading on the solvent were lower with models that used the empirical-based extraction equation versus the models that used the mechanistic-based approach. The errors in the predicted equilibrium pH values were quite similar for both systems. The latter was to be expected because both approaches used the same equations and equilibrium constants to describe the aqueous phase equilibria.

The models were compared in terms of the average errors of the predicted cop¬per loading on the solvent and the equilibrium pH of the raffinate because of the importance of these two quantities in characterizing solvent extraction systems. The overall average errors in predicted copper loading and equilibrium pH for the empirical and mechanistic approaches were 3.09 pct and 0.14 pH unit, and 4.57 pct and 0.13 pH unit, respectively. In almost all cases, models using either approach converged without problems. Models based upon both approaches produced overall average errors in the predicted copper loading that were within the target range of <5 pct error; however, the models that used the empirical-based extraction equations usually appeared to be more accurate. For this reason, the empirical-based approach for the extraction of copper and ammonia was emphasized in the models over the mechanistic approach.

It should be noted that the copper and ammonia extraction equations, equation coefficients, and equilibrium constants for the empirical- and mechanistic-based models were developed from data in the sulfate system. These models were applied to both the sulfate and carbonate systems with essentially the same accuracy (table 2). The application of the models to data that were not used in the model development demonstrates the accuracy and flexibility of the extraction equations.

Empirical-Based Approach

The errors in the predicted copper loading on the solvent for the Cu-NH3-SO4 and Cu-NH3-CO3 models are shown on figure 5. In the majority of cases the mod¬els predicted the copper loading to within 5 pct of the measured values. Of the

separate 123 shakeout tests that were made with the 10- and 25-vol-pct extractants, the predicted values for copper loading exceeded the target range of <5 pct in only 18 cases. Errors in the predicted copper loading tended toward the positive side in the sulfate system and toward the negative side in the carbonate system. The errors in the predicted equilibrium pH tended toward the negative side in both systems. A detailed comparison of predicted results versus measured results is given in appendix F for a sulfate and a carbonate data set.

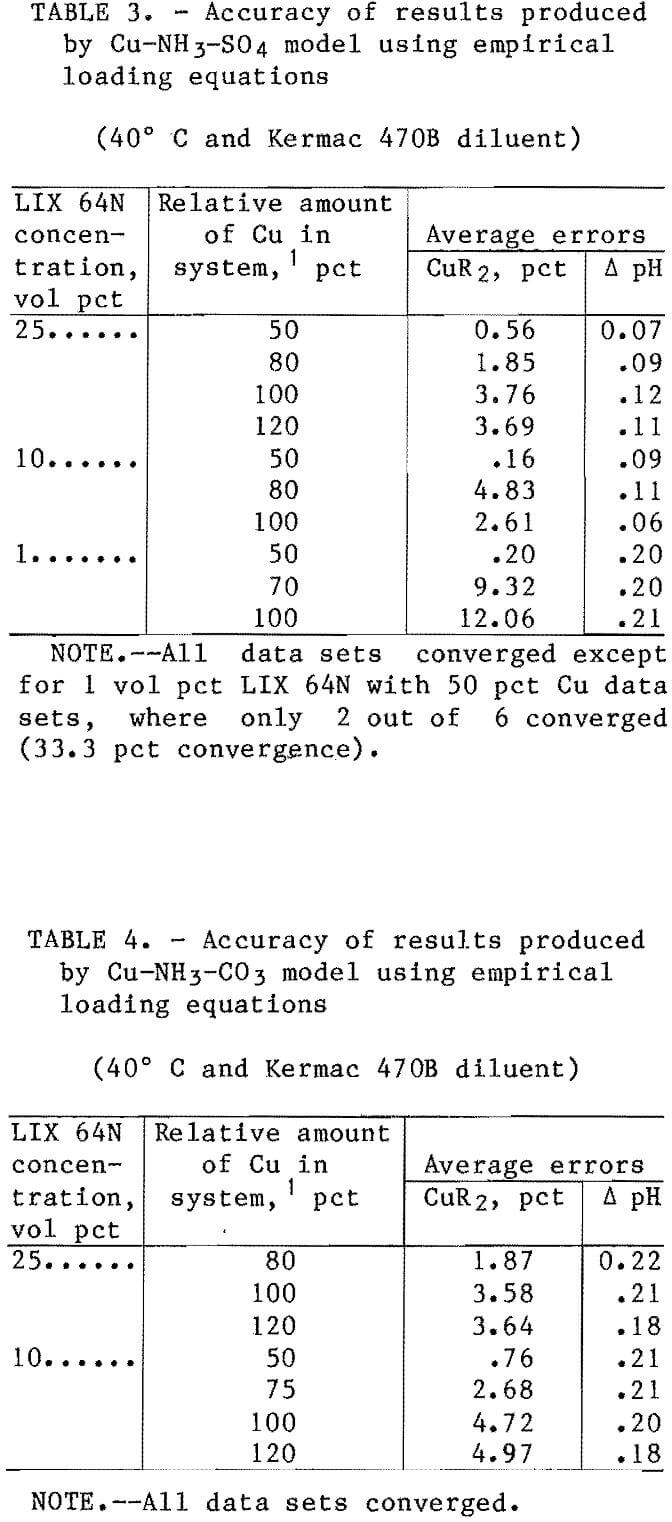
The results obtained from comparing the model predictions for copper loading and equilibrium pH against the observed results in the sulfate and carbonate systems are categorized and shown in tables 3 and 4. For informational purposes, the results were divided into groups that corresponded to different ratios of the amount of copper in the system relative to the maximum copper loading capacity of the solvent. For the majority of cases 4 each individual group represented at least six separate shakeout tests.

The test series were conducted at conditions of both high and medium anion concentrations and at three different pH levels (details discussed previously). In almost all cases, the average errors were within the target range of <5 pct error for the solvent loading. The exception was the data sets for the 1-vol-pct extractant. The errors in the copper loading on the 1-vol-pct extractants ranged as high as 19 pct; however,

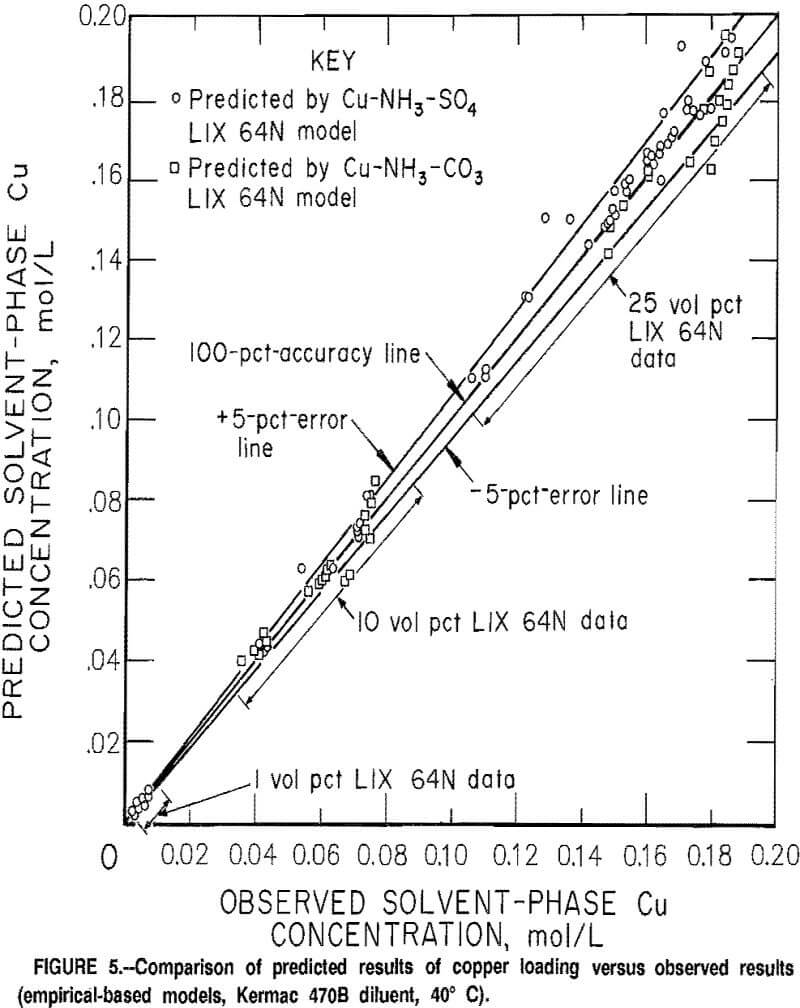
considering the relatively low value for the copper loading on the solvent (typical value was 0.004 mol/L), this was considered to be an insignificant error. The average errors for the predicted copper loading in the sulfate and carbonate systems with 10- and 25-vol-pct extractants were 2.51 pct and 3.17 pct, respectively. The average errors in the predicted pH of the raffinates were 0.10 for the sulfate system and 0.20 for the carbonate system.

The slightly reduced accuracy of the carbonate system model was likely caused by the previously mentioned aqueous phase complexities that were not accounted for in the model. These complexities included the formation of Cu-NH3-Y complexes (where Y may be HCO3-, NH2COO-, or similar compounds) and ignoring the effect of anion type on the values for the equilibrium constants. Generally, the models were more accurate at predicting copper loading at the lower loading levels (e.g., 50-80 pct) than at the higher levels. This was true in most of the systems investigated. Coefficients were also developed for the empirical-based extraction equations with a solvent containing LIX 64N and Kermac 470B at 25° C, and with a solvent containing LIX 64N and Solvesso 100 at 40° C. The Cu-NH3-SO4 model was tested with data sets from these two systems (table 5). The accuracy of this model with the data sets used was excellent. With the 25° C data sets, the average error in the predicted copper loading was 0.96 pct, and the average error in the predicted pH was 0.04 pH unit. With the Solvesso 100 data sets, the average error in the predicted copper loading was 1.44 pct, and the average error in the predicted pH was 0.10 pH unit.

Mechanistic-Based Approach

Models were developed that used mechanistic-based equations to describe copper and ammonia extraction. The results obtained from comparing these model predictions for copper loading and equilibrium

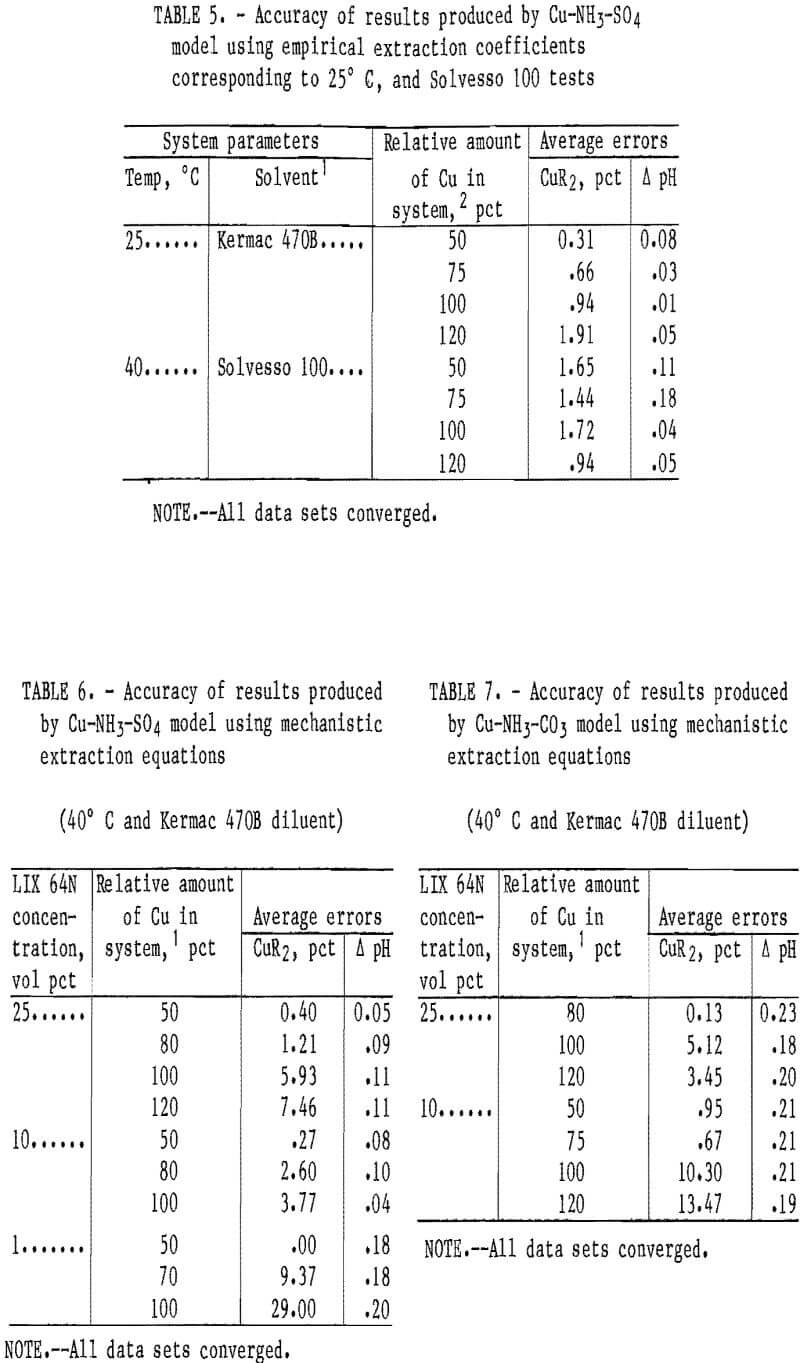
pH against the observed results in the sulfate and carbonate systems are shown in tables 6 and 7. With the Cu-NH3-SO4 model, the overall average errors in the predicted copper loading and in the equilibrium pH with the 10- and 25-vol-pct extractants were 3.64 pct and 0.09 pH unit, respectively (table 6). Generally, the errors in the predicted copper loading increased as the amount of copper in the system was increased. This trend was also observed in the models that used the empirical-based extraction equations. The results shown in table 6 correspond to 90 separate shakeout tests.

The Cu-NH3-SO4 model was also tested with data from tests with a 1-vol-pct extractant. The average errors in the copper loading and in the equilibrium pH were 12.79 pct and 0.19 pH unit, respectively. As with the previously described empirical-based model, the result for copper loading exceeded the error target. However, as previously stated, considering the relative size of the value for copper loading on a 1-vol-pct extractant, this represented an Insignificantly small error. The 1-vol-pct extraction system was outside of what industry would likely consider to be an economical range, but was only included in this report as a test of the models to demonstrate their useful range.
The Cu-NH3-CO3 model produced overall average errors in the predicted copper loading and in the equilibrium pH of 4.87 pct and 0.20 pH units, respectively (table 7). The overall average error in the copper loading was within the target- range error of <5 pct. However, as in the sulfate system, the average errors of the predicted copper loading were lower for the models that used the empirical- based extraction equation. The Cu-NH3-CO3 model with the mechanistic-based equations did not accurately predict copper loading for the 10-vol-pct extractant at conditions where relatively large amounts of copper were present in the system. The reason for poor prediction in this particular situation is not known.

P5100 Extractant

Models for the sulfate and carbonate systems were developed for the P5100 extractant with empirical-based extraction equations. Based upon previous experience in the LIX 64N system, it was decided to concentrate the modeling effort in the P5100 system only on the empirical-based extraction equations. Coefficients were developed for these equations with solvents containing P5100 and Kermac 470B at 40° C in the Cu-NH 3- SO4 system. Results from operation of the Cu-NH3-SO4 and Cu-NH3-CO3 model with appropriate P5100 data-sets are shown in table 8. The accuracy of the Cu-NH3-SO4 model with coefficients and data from the P5100 extraction system was reasonably good. The results from the 10- and 25-vol-pct extractants were combined and the overall average errors in the predicted copper loading and in the equilibrium pH were 3.95 pct and 0.12 pH unit, respectively. The accuracy of the Cu-NH3-CO3 model with coefficients and data from the P5100 extraction system was better than that experienced in the sulfate sytstem. This is somewhat surprising since the extraction coefficients were developed in the sulfate system and then applied to the carbonate system. The results from the 10- and 25-vol-pct extractants were combined and the overall average errors in the predicted copper loading and in the equilibrium pH for the carbonate system were 1.24 pct and 0.15 pH unit, respectively.

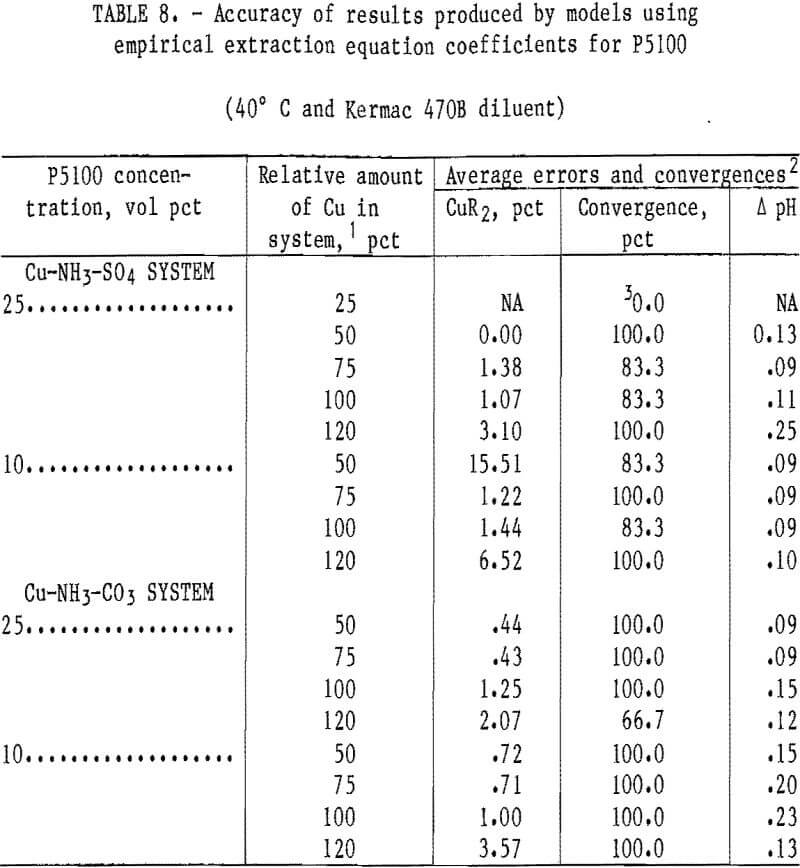
Generally, the two models using empirical-based extraction equations were very accurate in the P5100 system. Some problems with nonconvergence and/or relativity large errors in the predicted cop¬per loading were experienced with the Cu- NH3-SO4 model at some of the low solvent loading levels (25- and 50-pct levels).

However, low solvent loading levels such as these would likely be considered by industry to be below economical levels. Therefore, it is unlikely that the problems mentioned would severely limit application of that model in practical situations.

Summary

A mathematical modeling method was developed by the Bureau of Mines for the prediction of copper extraction from ammoniacal solutions. The research protocol that was used for determining the coefficients and equilibrium constants for the equations used in the models is presented. These coefficients and equilibrium constants were developed from data in the Cu-NH3-SO4 system. Variations of the models were successfully applied to the Cu-NH3-SO4 and Cu-NH3-CO3 systems with LIX 64N and P5100 solvents. Both empirical- and mechanistic-based equations were developed to describe copper and ammonia extraction. The models depended upon the simultaneous solution of equation sets for the nonlinear systems. Industrial-level concentrations were used in the investigations for the various constituents to allow direct application of the models to practical systems. The models were developed and/ or tested with data that represented a wide range of copper loading levels on the solvent (25 pct to essentially 100 pct of maximum capacity). The models required only limited initial solution parameters in order to accurately predict the extraction of copper as well as other associated equilibrium quantities.

The overall average errors in the predicted copper loading on the solvents were within the target-range error of <5 pct for all models described. The models had acceptable accuracies for most of the industrial-level conditions studied.

However, models that used the empirical-based extraction equations were slightly more accurate in predicting copper loading than their mechanistic-based counterparts. The overall average errors in the predicted copper loading and equilibrium pH for models in the sulfate and carbonate systems using the empirical extraction equations were 3.09 pct and 0.14 pH unit, respectively. These results pertained to copper extraction with solvents containing LIX 64N and Kermac 470B at 40° C. Systems with P5100 extractant, Solvesso 100 diluent, and at 25° C were also investigated and modeled with equal or better accuracies. Copies of the computer programs used can be obtained from the Bureau.