Table of Contents
The factors governing the determination of capacity for any open circuit crushing stage are much the same as those we outlined in connection with the secondary stage. In a properly designed crushing plant, excepting those plants which by-pass a portion of the pit-run around the head end of the flow line and inject this fraction back into the system at one of the reduction stages; the open circuit tonnages decrease from stage to stage, because fractions of the flow which are finer than the setting of each stage are scalped off and bypassed around it. Sometimes finished-product fractions are taken off immediately after the primary, or secondary, stage and sent directly to the finished-material storage; this bleeding off of finished material may also be carried on at each scalping point in the flow line. These various possibilities in flow diversion, and re-entry, point clearly to the necessity for preparing a complete flowsheet of the proposed plant before attempting to calculate the required capacity of any crushing stage. Only by doing this can we hope to approximate the requirements for the different stages.
The facts on which we base our flowsheet must of course be reasonably accurate if the flow-sheet itself is to be of any value. Admittedly, the true facts are sometimes difficult, if not impossible, to compile for a new operation. This is quite likely to be the case in opening up a new gravel deposit, unless a very thorough, and costly, system of development work is conducted before the plant is designed. Another unpredictable factor is that of the market for various sizes of product. It is a factor which has a very direct and marked influence upon the flowsheet, particularly upon the amount of work to be accomplished in the reduction crushers.
These uncertainties all indicate quite definitely the need for flexibility in the design of the crushing plant, especially those plants designed for the production of commercial aggregates, and this need is probably more important as regards the reduction crushing stages than anywhere else in the flow-sheet. The attainment of this flexibility does not necessarily entail the installation of an abnormally high amount of excess capacity, over and above the figures indicated by the flowsheet calculations. If the plant is arranged so that reduction-crushing capacity can be added conveniently, as and if required, we have the flexibility we need, and the margin of capacity to be provided in our selection of crushers need not greatly exceed the predicted maximum as determined from the flowsheet.
We can very seldom pick a crusher, or a battery of them, that will have exactly the rated capacity to match our calculated requirement for any given stage; and if we could do so it would not be sound practice to hew that close to the mark, because it is not practicable to maintain a crushing stage at its full-rated capacity 100 percent of the time. If we have an ample surge storage ahead of the stage to insure continuous feed we need only compensate for decrease in capacity due to mechanical causes. From 10 to 15 percent should take care of this.
Closed Circuit Reduction-Stage Capacities
Thus far we have considered open-circuit crushing through the several reductions in a multi-stage crushing plant. Very rarely are we able to turn out a finished product without closing the flow-line circuit somewhere along the line. Without going into any argument for or against closed-circuit crushing in any of the various stages, let us examine just what effect closing the circuit will have upon the required capacity for any particular stage.
Consider, for example, a single gyratory crusher of any type, arranged to operate in closed circuit with a vibrating screen, and set so that 70 percent of the original feed will be crushed to a size that will pass through the screen openings. Also, for the sake of simplicity, let us assume that the screen will take out all of this 70 percent undersize, i.e., will perform at 100 percent efficiency. Then, for each 100 tons of original feed to the crusher, 70 tons will pass on as finished product, so far as the stage we are considering is concerned, and 30 tons will return to the crusher, on the first pass.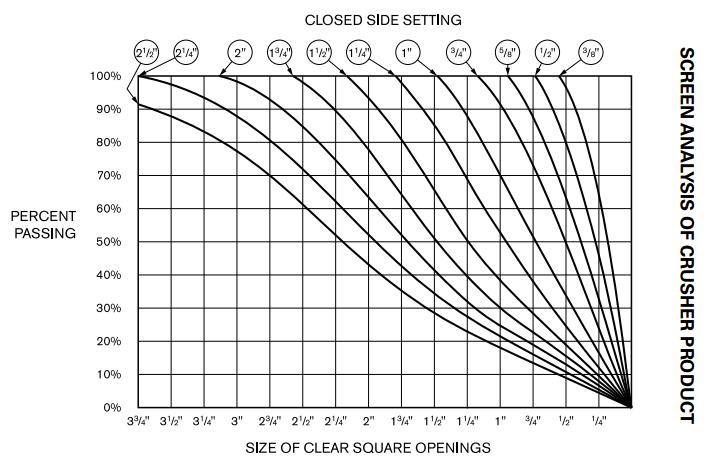
Now, we have to make another assumption, which probably is not strictly in accord with actuality, but seems to be close enough to the mark to suit all practical purposes: we assume that the material returned to the crusher in the first, or any succeeding, pass will be processed in exactly the same fashion as the original feed, i.e., crushed to the same percentages of undersize and oversize. On the basis of this assumption, we would crush 70 percent of the 30-ton fraction to finished Size, returning 30 percent, or 9 tons, to the crusher. At the next pass we obtain from this 9-ton fraction, 6.3 tons undersize, and 2.7 tons oversize.
 The process can be worked out by simple arithmetic to a fairly close approximation by calculating three or four passes; but it will be evident to the mathematically-minded that a simple convergent geometrical series is involved, which can be expressed by the formula:
The process can be worked out by simple arithmetic to a fairly close approximation by calculating three or four passes; but it will be evident to the mathematically-minded that a simple convergent geometrical series is involved, which can be expressed by the formula:
(I) T=100/(1-R)
where T = total load, and R=proportion of oversize in crusher product, expressed as a decimal. For the problem outlined, this formula sets up as follows:
T= 100/(1-0.3) = 142.9 tons
Thus, whereas we are dealing with only 100 tons of original feed, we must for the closed-circuit operation, set up crushing capacity for at least 142.9 tons, or 42.9% circulating load.
Crusher’ Screen Efficiency Factor
It should be noted that formula (1) is applicable only for 100 percent screen efficiency, something that is rarely, if ever, achieved in practice. So, to put the formula in more usable form, we must insert another factor to compensate for screen efficiencies below 100 percent. To illustrate why this is necessary, assume a screen efficiency of 90% for the problem just discussed. Then, on the first pass, the screen would reject, as oversize, 30/0.9=33.33 tons; and this same differential would apply to each succeeding pass. The revised formula takes the following form:
(II) T = 100 / ( 1 – R/E)
where E = screen efficiency, expressed as a decimal. Our problem now appears as follows :
T = 100/(1-0.3/0.9) =150.3 tons
which indicates a circulating load of 50.3%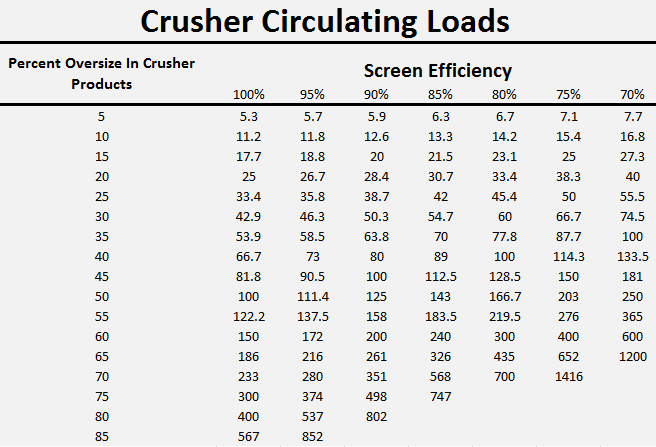
To present in convenient form values derived from formula (II), the above Table was prepared, herewith, showing theoretical circulating loads, expressed in percentages of the original feed. The table covers a wide range of oversize percentages in the crusher product, and several screen efficiencies. It is broad enough to cover almost any combination of conditions that might be encountered in actual practice.
How Much Circulating Load
In designing a closed-circuit crushing stage, the question of how much circulating load should be carried is a very important one. It not only has a direct bearing upon the capacity of the stage; it determines the amount of screening surface, and the elevating capacity necessary to handle the load in the circuit. There is no “blanket” answer to this question. It must be analyzed for each case, on the basis of the operating characteristics of the particular size and style of crusher that is being considered for the job.
Usually, when we set up a closed- circuit crushing stage, we want to get as many tons of finished material from it as possible or, conversely, we want to do the required job with as little outlay for crushers and screens as possible. We know the size of product the stage is to turn out, and we should know, to a fairly close approximation, how many tons of original feed are to be processed, and the size of this feed. Having this information we can, with the aid of the product tables and curves, and the circulating load table—or formula—analyze the problem for any crusher, or battery of crushers.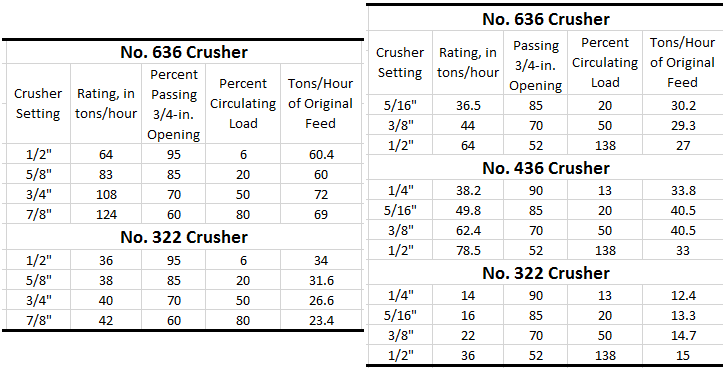
To illustrate how the analysis is made, as well as to demonstrate why the optimum setting may vary for different types of crushers, or for different sizes of the same type, the following examples have been worked out for two product sizes, using the Type “R” crusher for example.
 Assume, for example, that we are to crush a material, in a closed-circuit crushing stage, to pass a 3/4″ square opening (as determined by a flat testing sieve); that our screen, which forms a part of the circuit, will be fitted with the proper size of openings to make this 3/4″ product, and will be capable of performing at 90% efficiency. Also assume that the material is such that the crusher selected will crush it to a size, 70% of which will pass a square-opening test sieve equivalent to the close-side crusher setting. This can be determined either from tests made on the material, or from the table of approximate values presented in a foregoing section.
Assume, for example, that we are to crush a material, in a closed-circuit crushing stage, to pass a 3/4″ square opening (as determined by a flat testing sieve); that our screen, which forms a part of the circuit, will be fitted with the proper size of openings to make this 3/4″ product, and will be capable of performing at 90% efficiency. Also assume that the material is such that the crusher selected will crush it to a size, 70% of which will pass a square-opening test sieve equivalent to the close-side crusher setting. This can be determined either from tests made on the material, or from the table of approximate values presented in a foregoing section.
Using this 70% value as a basis, we first set up, from the product curves for screened feed, herewith, a column of percentages that can be expected to pass the 0.75″ opening, using as many trial crusher-settings as we wish (usually three or four will do). This column should be set up opposite the corresponding crusher settings, along with another column showing the capacity ratings, of the particular machine under consideration, at each of these settings. Having tabulated this information, we consult our table of circulating loads, or use formula (II), and list a fourth column of figures, showing the percentages of circulating loads which can be expected on the basis of the values in column 3, and for 90% screen efficiency.
A final calculation is now performed to arrive at the amount of original feed which, when added to the circulating load, will equal the capacity rating of the crusher at each trial setting. The formula for this calculation is:
(III) Tones of fresh feed = Crusher Capacity / ( 1 + Circulating Load in Decimal)
The following: tabulation shows how the problem works out for two sizes of the Type “R” crusher. It is interesting to note that the settings for maximum output, i.e., tons of original feed, are not the same for these two machines. These figures indicate that maximum output may be expected from the No. 630 crusher at a setting equal to the product size, whereas, the No. 322 machine shows up best at setting. If we wish to obtain this maximum performance from the larger machine, or from a battery of them, we must provide screening area sufficient to handle 1.5 times the original feed rate. For the smaller machine we need provide only 1.06 times the original feed rate.
Closed Circuit Crushing Calculations
As a further illustration of the process, the following tabulation covers the calculations for three machines of the same type, in closed-circuit with screens fitted for 3/8″ product, and operating at the same efficiency of 90%. In each of the above cases we have carried the tabulation through to a crusher setting slightly in excess of the product size, and in one case (the No. 322 crusher on 3/8″ products) the figures indicate maximum output at this plus-product setting. However, plus-product settings are not recommended for either standard gyratory crushers or reduction crushers of standard, or short, throw types, and figures for such settings cannot be considered as reliable. The reason this is so will be clear when we consider Just what kind of particles constitute the circulating load in a closed-circuit system incorporating any crusher of the pressure type.
High-speed, short-throw crusher, such as the Type R or cone, will reduce practically all of its product to a one-way dimension not exceeding the close-side setting of the crusher; hence, in a closed-circuit operation, if the crusher-setting is anything less than the square-opening product size, practically all of the material will be crushed, (hiring the first pass, to a size which is less than the screen opening, in at least one of its dimensions. Now, if all of the material were broken in cubical shape, and our screen operated at 100% efficiency, there would not be any circulating load for any minus-product- size crusher setting. It follows, therefore, that the entire circulating load, except that portion of it which is due to less-than-perfect screen efficiency, must consist of pieces that are more or less flat in shape. It follows, also, that these pieces will not be gripped by the crusher in any succeeding pass, unless they happen to fall in edgewise, and that most of them must be broken by being crushed between one of the crushing faces and some other particle of material. That they are so broken is evident; else the circuit would soon be choked with over-size pieces. Most of the particles which have a one-way dimension smaller than the product size probably require only one crack to reduce them to under-size, because the break need only be made in one direction: through the small dimension. On the other hand, if the crusher is set to a plus-product size, the over-size “flats” must be shattered in two directions to reduce them to under-size. Theoretically, the amount of work that must be done on these plus-product-size flat spalls is at least triple that which is required to break down the minus-product-size spalls. When we consider that most of this over-size breaking must be accomplished by catching the pieces against another particle, or particles, we can see why our figures, which work out quite well for minus-product-size crusher settings, cannot safely be used for plus-product-size settings. The circulating loads, for such settings, are apt to be inordinately high, and there is nothing to be gained by running the crusher that way, except, perhaps, on extremely soft and easy-crushing material.
Whether or not it is advisable to set the crusher to a discharge opening equal to the product size depends upon the crushing characteristics of the material. If the material is friable, or if it cubes well, it is safe to assume that the crusher can be so set; on the other hand, if it is hard, or tough, or tends to slab in the crusher. the setting should be held to a maximum of 80 to 85% of product-size, regardless of what bur figures indicate in the way of capacity for any coarser settings.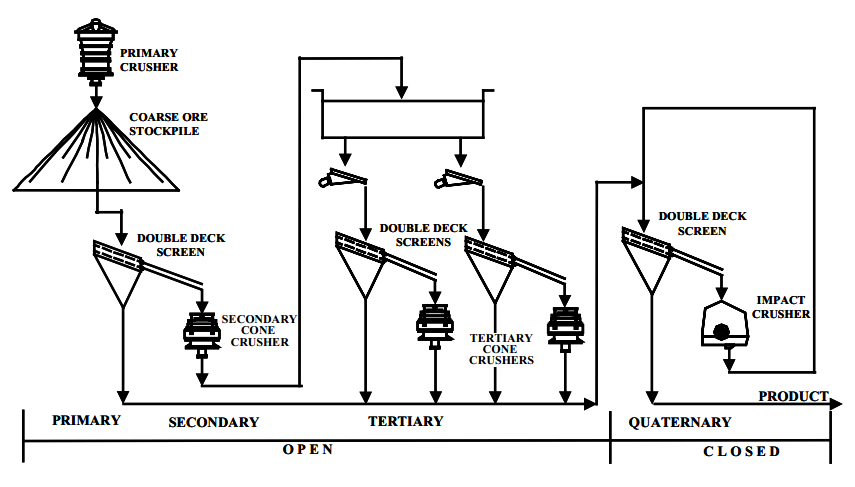
“Stage-crushing,” as we use the term here, applies to open-circuit reduction in a flow line comprising two or more crushing stages, with scalping between each stage, but without close-circuiting any stage upon itself; except, perhaps, the final one. Generally speaking, such an arrangement works out more efficiently than one in which each stage is run in closed circuit. There is nothing to be gained by sending oversize rock back to the crusher that let it go through once, unless the stage is the final “clean-up” stage in the flow line. The oversize should go on to a stage wherein the setting is smaller, and where these oversize pieces will be crushed by positive metal-to-metal contact. The scalping between stages in such a system should remove most of the material which is smaller than the setting of the next following stage.
