I happen to be one of those who believe that Rittinger probably meant what he said when he wrote what Stadler has quoted, “the increase of the surfaces exposed is directly proportional to the force required for reducing” “and therefore also to the work absorbed in effecting the separations.” (The italics are now mine instead of Rittinger’s or Stadler’s.)
Our difficulty lies in not understanding just what occurs at the so called “elastic limit.” Up to this point the energy applied to the body is absorbed by it uniformly in proportion to volume. At the so-called elastic limit the first break occurs some place within the body, releasing the energy locally absorbed at the point and allowing a further deformation without a proportional amount of energy being absorbed. The cause of the first break within the body is that the ultimate strength of a single crystal, or of the bonding material between crystals, was exceeded. A series of these “ local” breaks occur in sequence throughout the body until at some point several of these breaks lying close together so weaken it that the remaining crystals and bonding material are unable to resist further and the section fails, a fracture being the result. And except as energy has been absorbed in making these breaks,and any heating of the material has caused radiation losses, the individual crystals of the rock are allowed upon release of the pressure to return to their original form (in conformity to Kick’s law, if I understand it aright), and in so returning to this original form they return the energy they contained.
How is this energy returned? Either in pushing (or pulling) back the crushing faces, or, in accordance with a more universal law of nature, attacking the weaker part of the organization and completing the breaks upon the parts that have increased load put upon them by breaks alongside them.
I can conceive of a condition in a body in which a few individual crystals or groups of crystals are so interlaced that when the body is deformed by external pressure, and that pressure is released, these few crystals are so held that they are unable to return to their original shape. And Kick’s law would apply to these, but the effect of the energy absorbed by these few crystals would have no appreciable effect upon the total of energy absorbed when actual crushing takes place.
I consider that the above reasoning applies to bodies in tension, shearing, or compression; it can be shown, I believe, that these three phenomena reduce to the same thing, the breaking of crystal or molecular bonds. I am quoting no authorities in support of my arguments, as it seems we have to be our own authority at times.
Mr. Taggart’s paper is a disappointment to me in that he gives no experimental data in support of his argument. His use of Eads’s experiment is not convincing; he has made an assumption that is unwarranted namely, that all the deformation remains in the rock after fracture.
Von Reytt’s experiments, which Mr. Taggart cites, were made with working crushing machines, in which there are big friction losses, in bearings mostly, the actual efficiency of which I consider to be less than 25 per cent., disregarding the energy spent upon the unmeasured fines, —0.1 mm. By efficiency I mean the ratio of energy absorbed by the rock to energy applied to the machine.
In his criticism of my arguments in The Crushing-Surface Diagram, he might have analyzed by Stadler’s method the two crushing-surface diagrams given as Figs; 4 and 5 in my paper. (The two cuts were transposed in making up the forms, and certain box areas were not marked thereon, although referred to on the cut.) A statement in my original copy that was edited out suggested such analysis by the members of the Stadler school. Provided my work was honest and reasonably accurate, a comparison of “E. U.’s” per foot-pound applied would be illuminating.
Answering Mr. Taggart, I do not presume to say that crushing takes place in commercial machines between offset faces as shown in the theoretical diagram I used to show the application of the law of Rittinger. I might have amplified it further by showing how the cracks actually occur in the breaking rock and how the broken pieces assume their original volume in accordance with Kick’s law. But my paper was written with the purpose of explaining a new tool for mill operators, and I was hardly prepared to take at that time the full burden of the defense of Mr. Rittinger. I did what I could, and as I look over that argument now, it looks pretty good to me.
But why “argify”? The place to prove whether either law applies to crushing operations is in the laboratory, and there upon machines which will enable us to determine the energy absorbed by the rock, not in commercial crushing machines.
Some data of this kind I have at hand. I may say that it is all favorable to the law of Rittinger, and that it will be submitted to the Institute shortly.
Hallet R. Robbins, Pullman, Wash, (communication to the Secretary).—It is with some trepidation that I venture to comment upon Mr. Taggart’s excellent paper, which has done a great deal to clarify a subject heretofore somewhat obscure. The arguments brought forward in support of Kick’s law are logical and convincing.
Mr. Taggart seems to have gone astray on those of his formulae which involve F, the “area of fracture with reference to unit,” or else he has not made his definition sufficiently clear. To my mind, F means the total area of all the planes of fracture which are assumed to pass through the unit cube, when this is broken into a number of smaller cubes of equal size. Using the notation of the original paper, the number of these planes of fracture is represented by the expression 3(U/S – 1). The area of each plane of fracture is U². The total area of fracture is then equal to 3U²(U/S – 1) which may be written 3U²(U-S)/S. The results given by this formula may be checked by inspection and a slide rule for those cases where the unit cube is reduced in linear size one-half, one-quarter, etc. For example to break into 64 cubes of one-quarter the linear size of the unit, it is readily seen there must be nine planes of fracture, each one (0.896)² or 0.8028 sq. in. in area; 9 x 0.8028 = 7.225, checking the figure in my table of constants.
Based upon the preceding formula for F,I offer the accompanying revised table of formulae for determining Stadler’s constants.

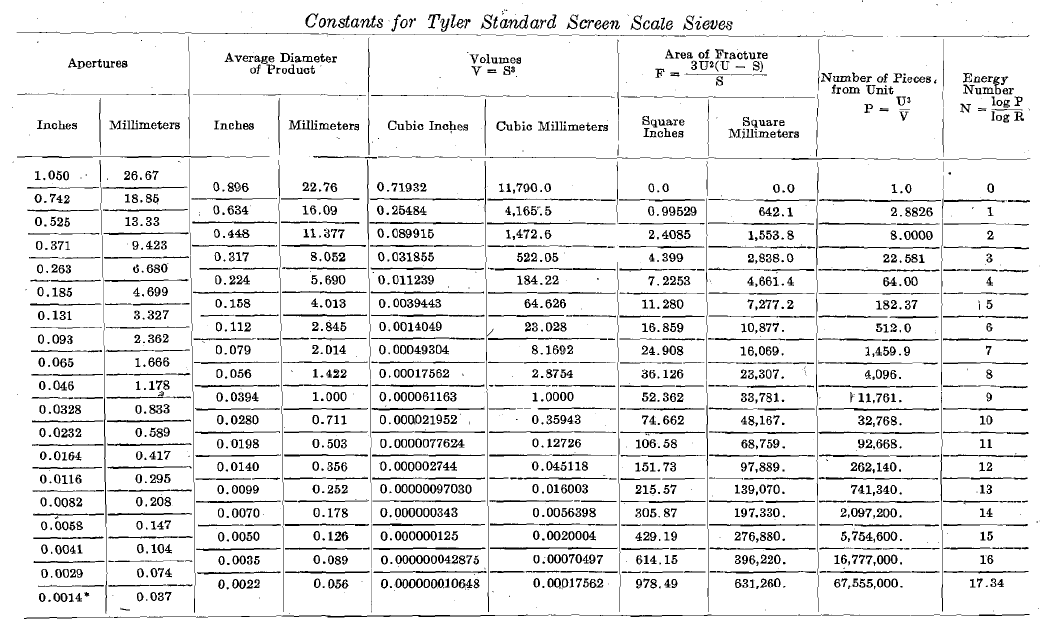
I have also calculated a table of constants for the sieves of the Tyler standard screen scale, based, not upon the aperture of the coarsest screen as a unit, but upon the average size of the product through the coarsest sieve on the next finer. The reason for this is that any product in a screen analysis consists of particles ranging in size between the apertures of the limiting screens. For all practical purposes it is proper to take as the average size of this product the mean of the apertures of the limiting screens. This is equivalent to assuming that the curve of crushing is a straight line between the points represented by two consecutive screens. A table calculated on the basis, of the average sizes of the successive screened products should be more generally useful than one based on the apertures. For the sake of uniformity, I have followed Mr. Taggart’s example in calculating the table to five significant figures, although three are all that is warranted, in as much as the screen apertures are accurate only to three significant figures, and in some instances even the third figure is inaccurate. The Energy Numbers in my table will not all be integers, if carried beyond three significant figures, fo
For the Tyler standard screen scale sieves, R =23/2 = 2.8284, log R = 0.4515450, and log (log R) = 9.6547010; r = 1/23/2 = 0.35355, log r = 9.5484500
W. J. Sharwood, Lead, S. D. (communication to the secretary) :- The author of this paper has done good service in attempting to clear
up, for the average mill man, some of the difficulties involved in an understanding of the rival “laws” proposed for comparing the work of crushing. It is regrettable that more exact experimental data are not available, and the hope may be expressed that such data may soon be forthcoming.
Hydrometallurgists must regret to see Rittinger’s law disproved, for surface exposed is, in general, a measure of the accessibility of solutions to ore; and this rule also ceases to approximate the truth only when the finest sizes are reached. If the premises are sound the author has evidently proved the case for Stadler’s Energy Units.
The fact that F is not absolutely equal to 3U3/S (as assumed on p. 168), but to 3U3/S — 3U2, does not apparently invalidate the proof in any way.
There appears, however, to be a flaw in the supplementary reasoning on p. 170, for if
W = 3 K C U6/V (7th line from foot)
and P = U3/V (from (2), p. 168)
we would have W = 3 K C U3 X P
where K , C and U have all been assumed as having constant values.
Hence W = constant x P
That is to say, the work done, in crushing a given weight of ore from any one stage to the next, would, from this reasoning, be proportional to the number of particles at the first of these two stages. If this were actually the case, the law deduced would give, with the finer sizes, extremely large work values, even larger than Rittinger’s increase of surface principle.
Apparently errors have been introduced in lines 13 to 16 from foot (p. 170), by assuming that the distance through which the force acts is C S; that is, that it is a constant product of the final dimension, rather than of the dimension before the breakage takes place. Again, in the next line we have: K F C S = work to rupture one particle, instead of all particles, although F has been previously defined as the fracture surface of the total number of particles derived from the original unit.
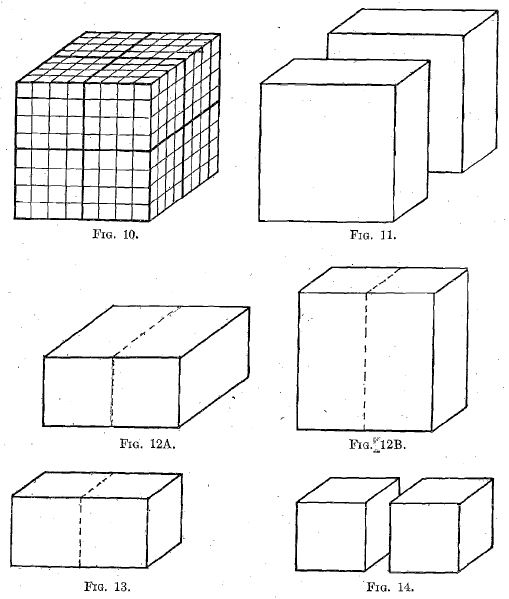
Crushing from one stage to another, several grades finer, may be effected in a number of ways. For instance, consider an 8-in. cube which is to be reduced to cubes of 1-in. edge. (1) It is conceivable that this might be done at one step, say by pressure applied at two opposite corners, breaking it, like Oliver Wendell Holmes’s one-hoss shay, “ all at once and all o’er,” into 512 1-in. cubes (Fig. 10). Or (2) by a similar application of force it might break at the first stage into eight 4-in. cubes, each of which might again be similarly broken, per saltum, into 2-in., and these again into 1-in. cubes. (3) A process of repeated bisection might be applied, the cube being first cleft into two 4-in. slabs, as in Fig. 11. These again may be bisected, either by a cut across a square face, as in Fig. 12A, or across a narrow face, as in Fig. 12B, each forming two “bricks” 4 by 4 by 8 in., which are broken crosswise into 4-in. cubes. The cycle is repeated to give 2-in., and again for 1-in. cubes. From reasoning on the lines’followed by Mr. Taggart, it would seem that the first method requires the greatest, and the repeated bisection the smallest, expenditure of energy. This indicates that, from the standpoint of work, fine crushing is best effected in several stages.
One source of difficulty in following the reasoning is due, I think, to the choice of the particular ratio of diameters adopted for the successive stages. In this connection the following quotations may be cited from Mr. Stadler’s reply to the discussion on his paper, as it originally appeared in the Bulletin of the Institution of Mining and Metallurgy:
“Just as coordinates, in analytical geometry, are a mere matter of convenience, so the determination of the sizes and steps upgrading is simply a question of convention. Once, however, we have adopted a particular standard of measurement, we must stick to it. I adopted the cube for the sake of mathematical simplicity. The sphere would have been equally suitable from a mathematical standpoint, but the reduction of a sphere to smaller spheres is not easily pictured in the mind, while the reduction of a cube to smaller cubes is easily imagined.”
“By reducing the cube of the unit successively to one-half of its volume, and assuming these fractions to be again of cubical shape, each size of this series of theoretical cubes obtained represents a grade of a reduction scale of the ratio 2.”
The successive diameters adopted by Mr. Stadler have, therefore, the ratio 1/∛2.
When breakage of a cube is, assumed to take place in a number of stages, at each of which the ratio of successive average diameters is the same; and if, as in the series considered by Mr. Taggart and by Mr. Stadler, this ratio is an irrational number such as 1/√2 or 1/∛2 it is a physical impossibility to carry out the comminution in practice.
If, for example, we assume the ratio of diameters to be 1/√2 or 0.707, and we attempt to carry out one stage of crushing on a single unit cube, we find that we get only one resulting cube of the theoretical dimension, and the same for each consecutive stage; the remainder of the mass is necessarily broken up into pieces of indefinite size. The same is true of the ratio 1/∛2.
A clear mental picture of the process, as suggested by Mr. Stadler, is undoubtedly desirable, but many people seem to find it difficult to conjure up a mental picture of one cube of rock being subdivided exactly into two cubes. It is, however, easy to understand the subdivision when the successive linear dimensions have a ratio corresponding to some simple fraction, preferably 1/2, thus giving stages of crushing which can actually be realized, as for instance by the breaking of a single unit cube into eight cubes—either at one motion or by three successive bisections, as illustrated in Figs. 10 to 14.
On account of this fact that most people, whose mathematical faculties are only moderately developed, find it easier to follow the reasoning where the reductions in size are physically possible, it would seem desirable to make the Energy Units conform to some integral ratio of diameters, preferably 2 :1 rather than V √2:1, and to make the intermediate values fractional.
This system has the advantage of simplicity, as it is easily remembered that each halving of the average .diameter means an addition of one unit to the ordinal number. Thus in the case of Mr. Taggart’s table (p. 171) the only change involved would be the division of all the numbers in the last column by two, each screen grade in the Tyler series corresponding to an ordinal number of 1/2. If Hoover’s ∛2 series of screens were adopted, each successive screen would mean an addition of 1/3 to the ordinal number. In a ∜2 series the addition would be 1/4, and so on.
