Table of Contents
A detailed experimental study of breakage kinetics in a batch rod mill indicates that while the system is inherently nonlinear, the feed disappearance kinetics for the finer sizes and the coarser sizes at high holdups is well represented by first-order behavior. The set of breakage distribution functions was found to be normalizable and independent of particle holdup in the mill. The size discretized initial breakage rate functions were found to be inversely proportional to particle holdup and almost directly proportional to particle size. A linearized grinding model that results from the first-order Taylor’s series expansion of the breakage rate expression was found to give good simulations of the mill product size distributions without recourse to any parameter improvement routines. Material transport through rod mills was evaluated by investigating the effect of operating variables on the holdup and residence time distribution of particulate solids flowing through the mill. Identical experiments performed in a continuous ball mill helped delineate the fundamental differences in particulate transport through these two types of mills. Mechanistic interpretations of the observed transport phenomena are presented, and their implications in the context of tumbling mill analysis and design pointed out.
Comminution or size reduction is usually the first step in the recovery of minerals from ores. In many respects, it is perhaps the most important step in the processing of ores. It plays a very important role in the performance of the mineral recovery processes that follow it because it determines the extent of liberation, the amount of fines produced, etc.
As ores become increasingly lower in grade and more refractory to treatment, comminution tends to become the single most energy consuming operation in a mineral processing plant. Consequently, there exists a considerable incentive to improve the efficiency of comminution operations.
Improvements in the operation and design of grinding systems are best achieved through detailed study of comminution processes in terms of phenomenological grinding models. This has been quite adequately demonstrated by the extensive research on modeling and predicting the behavior of ball mill grinding systems. Concurrently, however, little attention has been paid to the analysis of the equally important rod mill grinding systems. Thus, the specific objectives of this research program were to conduct a detailed investigation in order to
- delineate the fundamentals of rod mill grinding kinetics,
- study the application of a linearized grinding model to describe the nonlinear grinding kinetics in rod mills, and
- investigate the effect of operating variables on material transport through rod mills.
Linear & Nonlinear Grinding Models
During the past decade, considerable advances have been made in the population balance model description of comminution processes. This approach to the analysis of comminution processes entails the formulation of a mathematical model which is phenomenological in nature in that, for particles of a particular size and type (species), it lumps together the entire spectrum of stress-application events which prevail in a given mill under a given set of operating conditions. This viewpoint is especially useful for complex size reduction processes such as tumbling mills, for which it is presently impossible to specify the spatial distribution of the diverse types of breakage events. The development of phenomenological grinding models has been discussed in the literature previously and will not be presented here. It must be pointed out, however, that particular success has resulted from the analysis of batch ball mill performance in the framework of a discrete form of the time-continuous phenomenological model for a single homogeneous material. It utilizes mass balances in terms of mi(t), the mass fraction of particulates in the mill in the size range xi to xi + 1 , which have the form
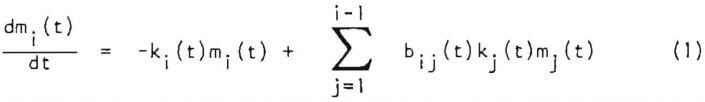
for i = 1, 2 to n, the size distribution being subdivided into n size fractions, Here xi/xi+1, and xj/xj+1 correspond to the Tyler sieve ratio, namely √2, a practical choice determined by the experimental procedures employed.
In Equation 1, ki(t), the size discretized breakage rate function, gives the fraction of material in the size range xi to xi+1 broken in the time interval t to t+dt. The size-discretized breakage distribution function, bij(t), represents the proportion contained in the size range xj to xj+1 of the product of breakage ( in time interval t to t+dt) of a unit mass fraction of a larger size fraction, xj to xj+1. The explicit time dependence of ki(t) and bij(t) is a formalism for representing the influence of changing mill environment on the breakage. It is by the dependence of these parameters on the mill environment that the linearity/ nonlinearity of the breakage process in a tumbling mill is determined.
In most situations of interest, the breakage distribution function, bij, is independent of the mill environment and the linearity of the breakage process in a batch mill is determined completely by the breakage rate function. Environment dependence of ki(t) then implies that the set of differential equations I is nonlinear for which no closed-form analytic solution exists. It has generally been observed that the breakage rate functions in dry batch ball milling are environment-independent, and the consequent linearity of breakage kinetics in these systems is a considerable advantage in their analysis, simulation and scale-up design. On the other hand, the “protection” of fine particles by the coarse particles between the rods in a rod mill leads to environment- dependent ki(t), a feature that considerably complicates the analysis of rod mill grinding systems. It is therefore necessary in this case to linearize the general nonlinear batch grinding model (Equation 1) and apply the analytic solution derived therefrom to the analysis of rod mill grinding. This topic will be discussed in detail in this report.
Extension of this model to open and closed circuit comminution relies on the assumption that the batch model, Equation 1, also pertains to size reduction in continuous mills. In addition, any simulation of continuous rod mill grinding must account for the influence of operating variables on material transport through the mill, a topic that will be dealt with in this investigation.
Experimental Methods
The experimental part of this program was aimed at performing a detailed analysis of the breakage kinetics in a batch rod mill in order to develop a better understanding of the breakage sub-process in a rod mill and to obtain the quantitative information necessary to study the applicability of the linearized batch grinding model to the mill/material system investigated. Specifically, mono-sized dolomite of various feed sizes was ground in a 12.7 cm diameter mill at various material loads to examine the effect of these variables on the breakage kinetics in the mill. By using appropriately designed end plates, the mill could be operated in continuous mode. Using hollow, lightweight Lucite rods charged into the continuous mill instead of steel rods, material transport characteristics could be clearly delineated in the virtual absence of grinding effects.
Batch Mill Experiments
All batch mill experiments were performed in a stainless steel mill that was 12.7 cm in diameter by 29.2 cm in length. The mill was lined with eight equally-spaced lifter bars 0.32 cm in length. It was also provided with 20.1 cm diameter flanges which rested on a pair of 7-6 cm diameter neoprene rollers, each supported by a pair of bearings. One of the rollers was driven by a Marathon constant speed motor through a Graham speed reducer.
Feed for the tests was prepared by crushing dolomite obtained from Kaiser Aluminium and Chemical Corporation, Salinas, California, in a jaw crusher followed by a roll crusher. A Sweco Air Separator was used to produce approximately 14 x 20, 20 x 28, 28 x 35, and 35 x 48 mesh material which was then sieved in small batches for one hour on a Rotap Sifter to get the √2 interval feeds. In addition, the 14 x 20 and 20 x 28 mesh feeds were split to obtain 14 x 16 and 20 x 24 mesh feeds to analyze the behavior of √2 interval feeds.
The rod charge to the mill in all experiments consisted of thirteen .9 cm diameter stainless steel rods, weighing 7-94 kg. This corresponds to a 40% filling of the mill internal volume by the rods at rest. The operating speed of the mill was fixed at 79 rpm in all cases, this speed corresponding to 61.4% of the mill critical speed.
The mill was layer-loaded with dolomite feed and rods to ensure well-mixed conditions during start-up. After grinding the material for 0.5, 1.0, 2.0 minutes, etc., the mill contents were discharged into a steel trough. Each of the rods as well as the mill insides was carefully washed with water to keep ground product loss in handling at a minimum. This is required at finer grinds, especially. The product was then wet sieved on a 400-mesh screen with a vacuum filter to collect the minus 400-mesh (wet) fraction and facilitate water drainage. The plus 400-mesh fraction was dried in an oven at 125°C and the dried product screened for 30 minutes on the Rotap Sifter using an appropriate deck of Tyler sieves.
Continuous Mill Experiments
The feeder/sampler setup for this part of the research program (shown in Figure 1) is identical to the one used in our research on continuous

Figure 1.-Photograph showing the continuous mill set-up. At the left is the feeding system which consists of two bins constructed to feed material at a constant head to a vibratory feeder. The mill rotates on two 7-6 cm diameter hard rubber rollers. As shown, the mill can be split longitudinally into two halves such that the upper half can be replaced by a sampler (shown in the background) to study the internal distribution of the holdup. A dust emission control chute is fitted around the discharge end of the mill. When a sample is to be taken, a gate is flipped so that the material flows into the continuous sampling device (foreground) which is rotated at a fixed speed so that samples can be collected at regular intervals.
ball mill grinding and has been described in detail in a previous report. The mill used was a 12.7 cm diameter stainless steel mill, identical to the one used in the batch grinding studies, but 43.8 cm in length. At the feed end of the mill, a 2.5 cm opening permitted introduction of the feed to the mill. Since the mill was operated in an open-end configuration, the discharge end was completely open, except for a wire grid to prevent balls or rods from falling out of the mill. Hollow Lucite rods of density 1.25 g/cm³ and 1.9 cm diameter were used to simulate the grinding media without any appreciable grinding action. To compare the material transport characteristics of rod mills with those of ball mills, identical experiments were performed with the mill charged with Lucite balls.
Material transport characteristics were delineated using the tracer impulse-response technique frequently employed in fluid flow studies. The tracer material was dolomite of the same size as the feed, but dyed with a food coloring so that it could be distinguished from the bulk material. The experimental procedure consisted of feeding the material to the mill under specified conditions until steady-state operation was obtained. At this point a tracer impulse was introduced at the inlet of the mill, and the discharge was sampled at regular intervals using the spinning sampler. When all the tracer had discharged from the mill, the mill was stopped and the holdup of material was measured. By counting the tracer particles in each sample, the tracer concentration (residence time) distribution was obtained.
Material Breakage Kinetics in a Rod Mill
Examination of breakage kinetics in a mill is made by studying the first-order feed disappearance plots. Figure 2 shows the first-order plot for the disappearance of 14 x 20 mesh dolomite filling 100% of the rod interstitial volume. The increasing slope of the curve as the grind progresses is indicative of an environment-dependent breakage rate function (which is the instantaneous slope of the curve) at this holdup level for this size feed. This behavior is typical of rod mill systems and has been observed in other investigations in such systems. In order to make a detailed assessment of this environment-dependence, the grinding of 20 x 28, 28 x 35 and 35 x 43 mesh feeds was examined. These are also shown in Figure 2. It can be observed that there is a distinct tendency towards linear kinetics behavior as the feed size is decreased. It appears, therefore, that the environment-dependence effects are themselves size- dependent and that the grinding kinetics of the finer sizes in a rod mill is adequately represented by first-order behavior (at least over the range of examination).
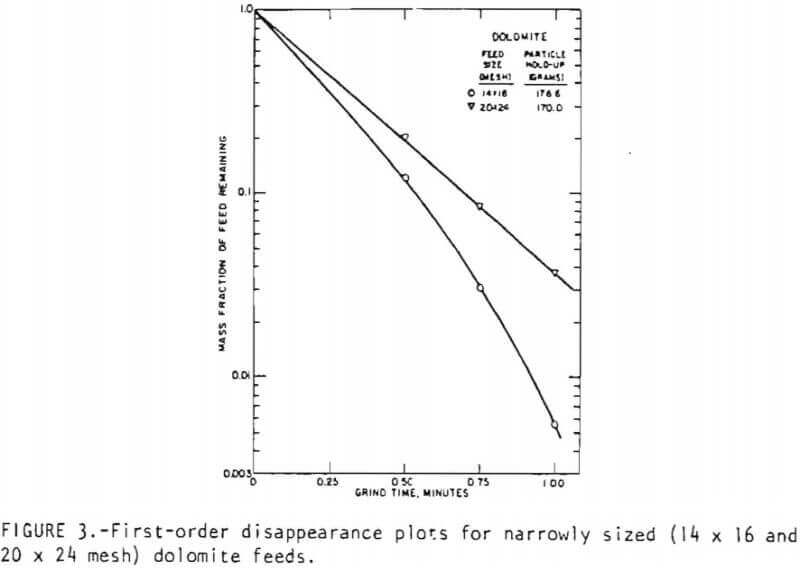
In light of these observations, it was decided to examine the effect of a smaller feed size interval on the grinding kinetics. The disappearance behavior of two 4√2 size intervals feeds is shown in Figure 3. The 14 x 16 mesh feed displays nonlinear disappearance behavior even over 1-minute of grind time. The 20 x 24 mesh feed exhibits linear behavior in agreement with the previous observations on the behavior of fine sizes in the mill. Figure 3 implies that use of a linear grinding model with √2 size intervals to simulate rod mill behavior would be inappropriate.
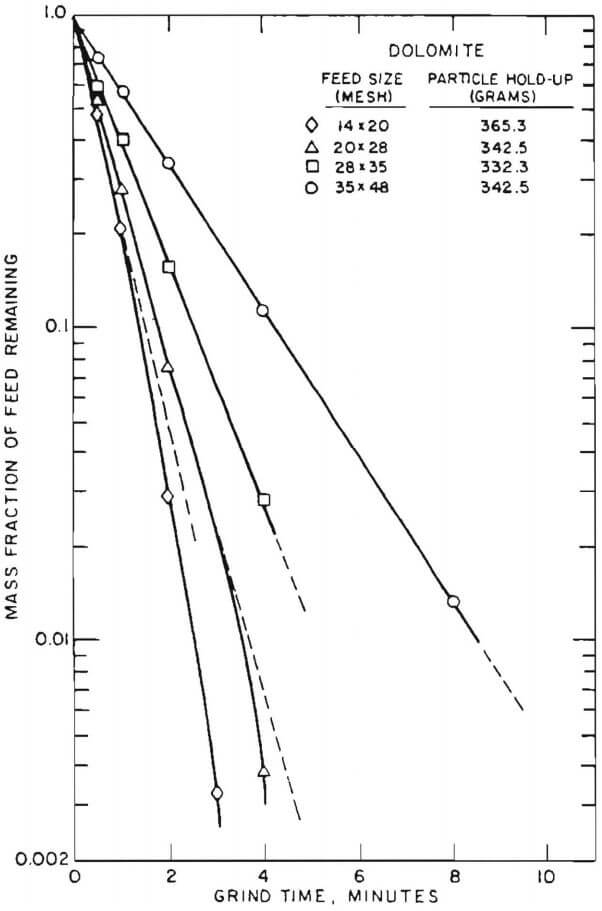
Figure 2.-First-order disappearance plots for the batch grinding of dolomite feed of different sizes. In all cases, the mill was charged with 1.9 cm diameter rods filling 40% of the internal volume of the mill with a feed loading equivalent to 100% of the rod interstitial volume.
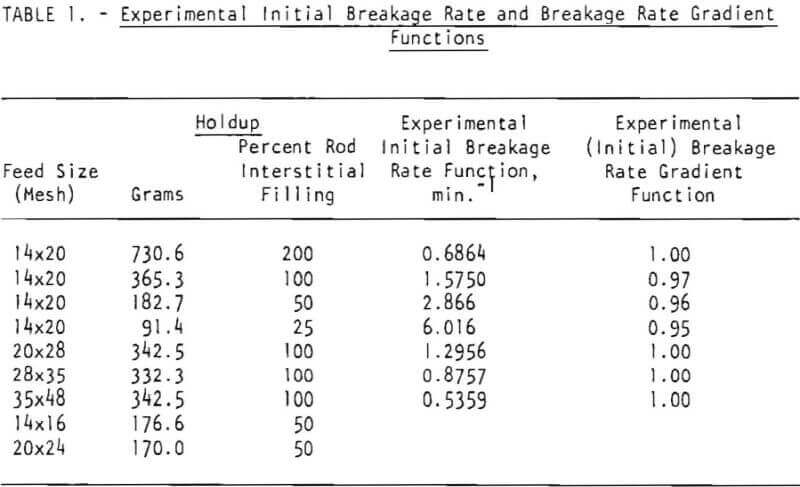
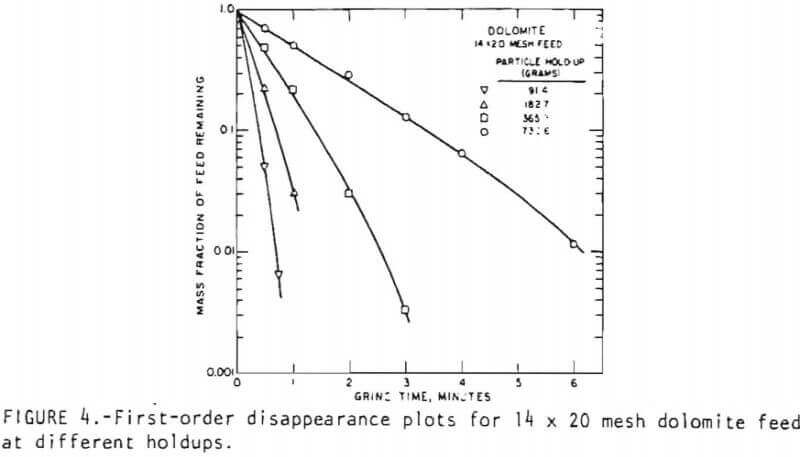 In general, the breakage rate function is expected to depend on the holdup of material in the mill. The effect of holdup was therefore investigated to examine this relationship. In view of the effect of feed size discussed above, the holdup in the mill might also be expected to influence the environment-dependence phenomenon. Figure 4 shows the effect of holdup on the breakage kinetics of 14 x 20 mesh feed. With increasing holdup, the feed disappearance kinetics tend towards first-order behavior. This can be seen most readily for the 731-gram holdup. Table 1 lists the set of breakage rate functions obtained from these experiments.
In general, the breakage rate function is expected to depend on the holdup of material in the mill. The effect of holdup was therefore investigated to examine this relationship. In view of the effect of feed size discussed above, the holdup in the mill might also be expected to influence the environment-dependence phenomenon. Figure 4 shows the effect of holdup on the breakage kinetics of 14 x 20 mesh feed. With increasing holdup, the feed disappearance kinetics tend towards first-order behavior. This can be seen most readily for the 731-gram holdup. Table 1 lists the set of breakage rate functions obtained from these experiments.
In either case, it is important to recognize the significance of these results. The foregoing discussion does not purport to imply that the inherent nonlinearity in the breakage kinetics in a rod mill can be ignored. Rather, it has been the intention to bring out the important observation that the breakage kinetics can be reasonably well represented by a first-order behavior for the finer sizes in the mill and at higher holdup levels for the coarser sizes. This phenomenon is particularly useful in the context of batch rod mill simulation employing a linearized grinding model, as will be illustrated’ later in this report.
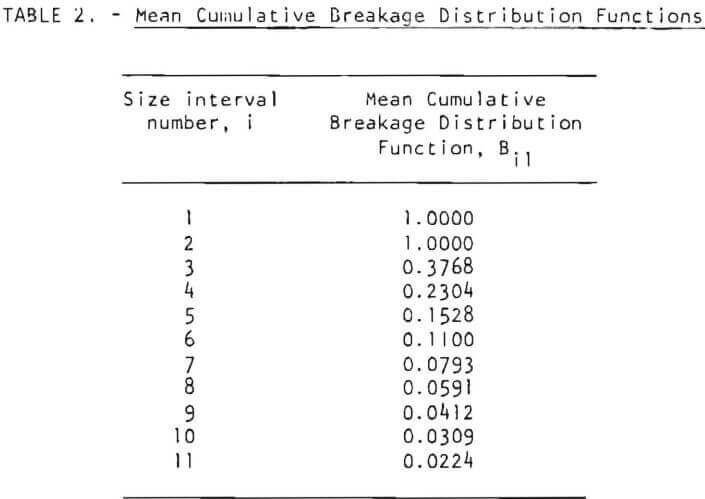
The breakage distribution function was evaluated from the zero-order fine particle production plots. The results indicated that, similar to the case in dry batch ball milling, the breakage distribution functions are normalizable (that is, independent of the parent size) and independent of holdup in the mill. Table 2 lists the mean values of the cumulative breakage distribution functions obtained. Details are given in the thesis by Swaroop.
A complete description of the kinetics of tumbling mill size reduction requires a knowledge of the nonfeed-size breakage rate functions also. Experimental data obtained in this research program indicated that for the; mill/material system under consideration, the initial breakage rate functions (initial slope of the first-order feed disappearance plot) satisfied the following relation
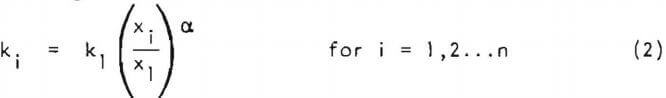
where ki = initial breakage rate function for the coarsest size fraction used (14 x 20 mesh), x. is the geometric mean size of particles in the i-th size interval. The exponent α was found to be 1.04.
A regression analysis of the breakage rate function data at different holdups of 14 x 20 mesh feed indicated that the following inverse linear relation is valid:
kl = β/H…………………………………(3)
with β = 614.9 g/min-1 (H in grams and kl in min-1)
Equations 2 and 3 can be combined to give a predictive scheme that
incorporates the effect of particle holdup in the form

where xi refers to the geometric mean size of the 14 x 20 mesh interval. This equation has considerable advantages in mill simulation because it can be used to ‘predict’ the required set of initial breakage rate functions at any holdup.
The Linearized Batch Grinding Model
As already discussed, if the breakage rate functions, ki, i = l, n, are dependent on the size distribution of the material in the mill, the batch grinding model (Equation 1) is nonlinear and the convenient analytic solutions and analysis that apply for linear grinding systems (see, for example, 11, 12, 18) are not valid in this case. It is therefore necessary to examine comminution kinetics in systems characterized by environment-dependent breakage rate functions such as rod mills in terms of a linearized grinding model that provides an appropriate framework of a practical analytic solution. In this section, the important features of this approach to rod mill analysis are presented.
Linearization is a commonly used technique in the modeling and analysis of engineering systems. Many engineering systems display nonlinear characteristics in all or a part of their operating range. Since linear formulations lend themselves to relatively easier analysis and possess greater flexibility, it is a frequent practice to linearize the nonlinear state equations around a suitable reference state (which is usually the initial state or the “equilibrium” state). A very useful mathematical simplification is usually achieved by linearization; however, depending on how strong the nonlinearity of the system is, the linearized state equations can describe the state of the system reasonably accurately only in a certain “region” around the reference state. Prudence must therefore be exercised in the application of linearized formulations to the description of the state of the system at large deviations from the reference state. It is therefore important in the context of the system under consideration to assess the range in which such a formulation will be valid.
A linearization scheme for the general case of environment-dependent breakage rate functions has been suggested by Herbst and Mika and is briefly outlined here. Basically, this entails making a multi-variable Taylor’s series expansion of the quantity ki[H;ml (t) , l = 1,n]Hmi(t) around a reference size distribution environment in the mill [mi(t), i = 1,n]:

Truncaction of the second and higher order terms in Equation 5 leads to the linear form of the breakage rate expression. Substitution of this into the system of n coupled differential Equations 1 (for i = 1,n) and reduction into matrix form gives:
d/dt [Hm (t)] = – {[1 – B] K∗ + γ} Hm∗ + γHm(t)……………………………..(6)
Here m(t) is a nxl vector of mass fractions, K* is a nxn matrix of the reference breakage rate functions, B is a lower triangular nxn marix of individual breakage distribution functions and γ is a nxn matrix with elements γip given by :

Equation 6 is the linearized form of the batch grinding model for which an analytic solution is readily available. The practical application of this solution is, however, highly restricted because of the formidable computational problems it presents. Simplification of the solution to a more useful form is achieved by explicitly assuming that the important first-order contribution to the breakage rate expression of any size class in Equation 6 comes from the gradient term with respect to the mass fraction in that size class, i.e.,

Linearization of the nonlinear grinding model thus introduces an additional parameter that is necessary for the description of the environment-dependent breakage process occurring in rod mills, namely, ∅ii, (or simply, ∅i). Because of its origin, it is proposed to call ∅i the breakage rate gradient function of the i-th size interval.
In the next section, the application of this linearized grinding model to the simulation of product size distributions obtained in a batch rod mill is presented.
Simulation of Batch Rod Milling using the Linearized Grinding Model
A computer program for the simulation of linear grinding systems had been developed in this laboratory under a previous USBM contract. This program was modified so as to incorporate the solution to the linearized model (Equation 9). The program can now simulate both linear and nonlinear grinding systems by appropriate specification of the breakage rate gradient functions.
In the context of the linearized model, in addition to the set of breakage rate and distribution functions, the breakage rate gradient functions must also be determined. The breakage rate gradient function can be evaluated from the first-order feed disappearance plots. Recalling Equation 9.
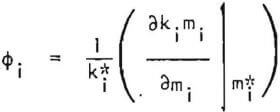
Hence the slope of a plot of kimi, versus mi (evaluated at a point corresponding to the reference size distribution) divided by the corresponding breakage rate function yields ∅i. It must be noted that for linear kinetics, ∅i = 1, so that there is no need to evaluate ∅i for the finer sizes for which first-order behavior has been observed. The breakage rate gradient functions obtained in this manner are given in Table 1.
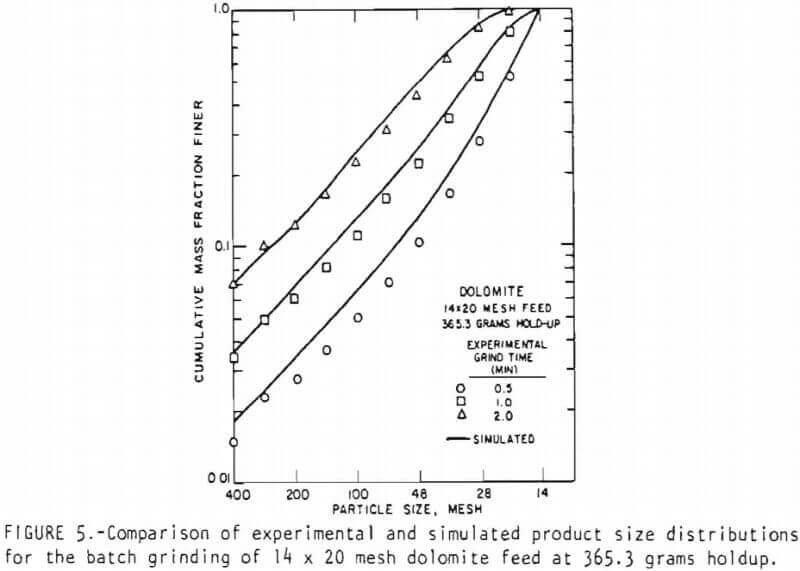
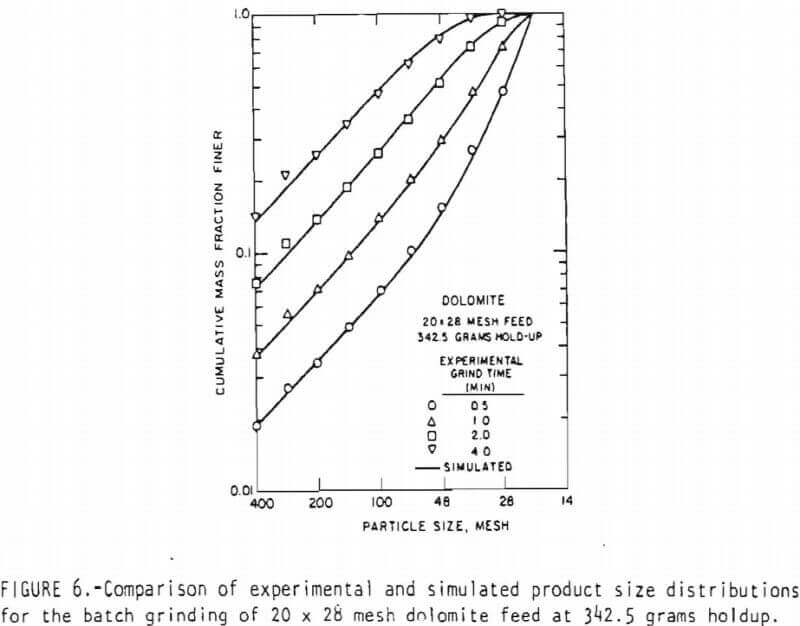
All simulations were performed on a C.D.C. 6400 digital computer, figures 5 and 6 represent typical comparisons between the experimental and simulated product size distributions. In general, the linearized model appears to describe the batch grinding behavior well. However, in Figure 5, the simulation of the 0.5 minute grind product using the predictive scheme for the breakage rate functions seems rather inaccurate. This appears to result because a slightly higher breakage rate function for the feed size is predicted by the scheme. During this short interval of grinding, the feed size breakage rate function dominates the product size distribution and so the simulation using the predictive scheme gives a finer size distribution for the product.
Perhaps the greatest advantage of using a linearized model to describe rod mill breakage kinetics lies in its potential to develop the (reference) breakage rate functions at any arbitrary feed size distribution from the mono-sized feed. Recalling Equation 8.
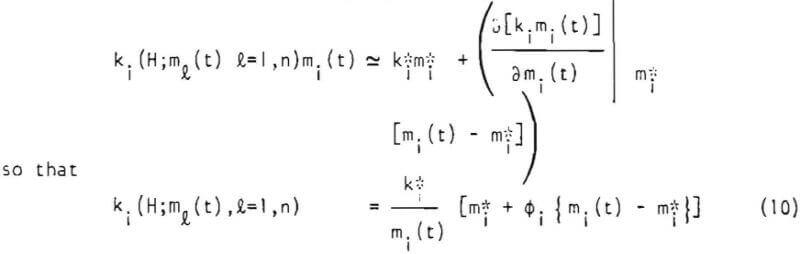
This equation permits the evaluation of the set of breakage rate functions at any desired environment size distribution in the mill if the reference breakage rate functions at another known mill environment are known. Using the mono-sized feed data, therefore, it is possible to estimate the the set of ki values for a distributed size feed. The application of the linearized model to describe the grinding of “natural” size distribution feed was studied using these concepts. Feeds for grinding were considered to be the mill products after 0.5 and 2.0 minutes of grinding 14 x 20 mesh feed at 365.3 grams holdup, respectively. Figure 7 is a typical comparison
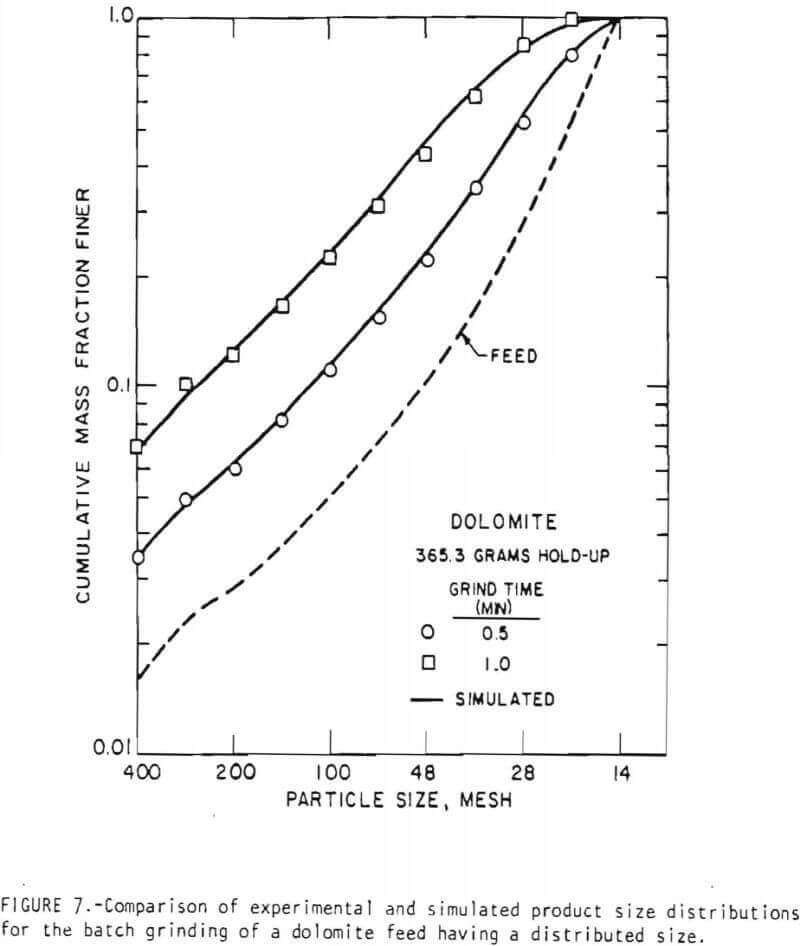
of the simulated results with experimental results. Note that the actual experimental grind times are (t + 0.5) and(t + 2.0), respectively, where t is the grind time shown. It appears, therefore, that the linearized model describes the grinding of a distributed feed quite well. These figures also demonstrate the influence of the reference state used in the evaluation of the breakage rate functions on the simulation. As is to be intuitively expected, the closer the reference state is to the simulated state, the better is the simulation.
Material Transport Through Rod Mills
A detailed, quantitative understanding of the characteristics of continuous rod mill grinding involves not only delineation of material breakage kinetics in the mill, but also material transport phenomena in the mill. In the past, little attention has been paid to the material transport sub-process in rod mills. The only relevant work in this regard is that of Heyes and co-workers who concluded on the basis of a few experiments that the contents of a rod mill are well-mixed. However, their results are not adequate for describing the transport characteristics of solids flowing through a rod mill. In order to clearly delineate rod mill material transport characteristics , it is necessary to examine in detail the effect of operating variables on material transport through rod mills. It was in this context that this aspect of the research program was undertaken. Before presenting the results obtained, it is necessary to briefly outline the theoretical basis for the experimental analysis.
Residence Time Distribution Analysis
In this approach, the quantity used to represent the material transport properties is the residence time distribution (RTD) of material in the mill E(t). It is defined such that E(t) dt is the number of fraction of the particulates in the effluent stream with ages between t and t+dt. The age of a particle denotes the length of time it has spent in the device so that E(t) is also the exit age distribution of material in the effluent stream.
It is often convenient to analyze material transport behavior in terms of certain parameters of the RTD. The two most useful are the mean, T, and variance, σ²τ, of the RTD for the tracer. The corresponding dimensionless RTD, E(θ), where θ = t/T is the dimensionless time, is characterized by the dimensionless variance:
![]()
The mean residence time of the bulk material, TB, is obtained directly from the mass flow rate of feed material to the device, F, and the holdup of material in the mill, H:
TB = H/F……………………………………..(12)
In principle, the tracer and bulk mean residence time should be identical, and in the present work it was observed that, within the limits of experimental accuracy, T = TB in all cases. As has been the relevant practice, an instantaneous pulse of tracer introduced into the mill at the inlet at an arbitrary time t = 0 was employed. The response to this stimulus at the outlet of the device is most conveniently represented in dimensionless form in terms of the so-called C-curve. This is given by C(θ)/co, where C(θ) is the concentration of tracer particles in the effluent at dimensionless time θ and the initial concentration of tracer, co, is a reference value which is calculated assuming the entire tracer pulse is distributed evenly throughout the device. Thus, C(θ) represents a dimensionless concentration. For an idealized impulse stimulus
C(θ) = E(θ) = τE(t)……………………………(13)
Thus, experimental determination of the dimensionless RTD, in conjunction with the use of an instantaneous pulse of tracer as a stimulus, requires only the evaluation of the dimensionless concentration C(θ), i.e. of the C-curve.
Quantitative analysis of particulate transport characteristics using tracer RTD data is accomplished in terms of a suitable mathematical model, such as those used successfully for the description of fluid flow process systems. Basically, two types of models were used to analyze the tracer impulse response (exit-age distribution or residence time distribution data), namely, the axial dispersion flow model and the tanks-in-series flow model. The parameters of these models can be easily determined from the dimensionless variance of the C-curve (σθ²) . Since mechanistic interpretations of particulate transport are most appropriately made through the parameters of the axial dispersion model, namely, the Peclet number (Pe) and the axial dispersion coefficient (D), this model was used for data analysis throughout this research program. For this purpose Pe and D are determined from σθ² using the relationships.

where v is the axial convective velocity of material flowing through the mill and L is the mill length. The Peclet number thus represents the ratio of convective transport to dispersive transport and the dispersion coefficient characterizes the intensity of dispersion in the system.
In the next section, the experimental results obtained on the effect of operating variables on material transport through rod mills in terms of the holdup and Pe are discussed. For purposes of comparison identical experiments were performed in a mill charged with Lucite balls and these results are also presented.
Effect of Operating Variables on Material Transport through Rod Mills
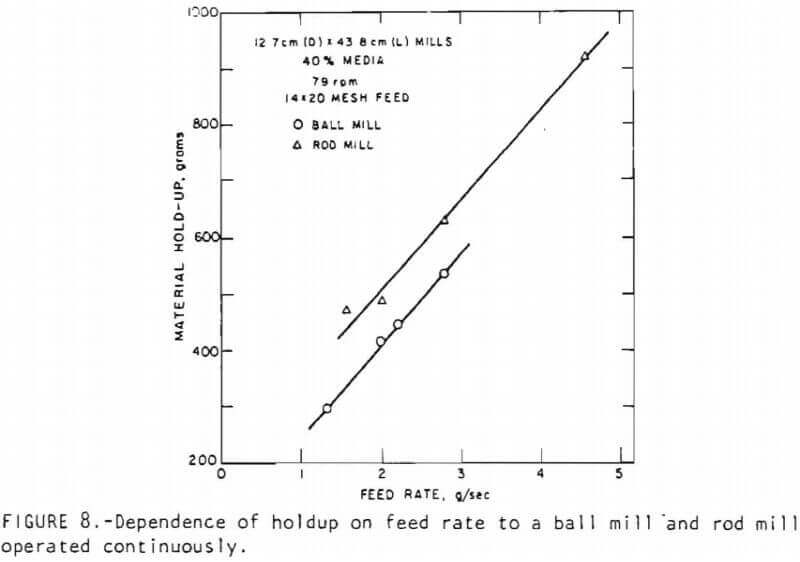
Effect of feed rate on holdup: Figure 8 presents the effect of feed rate on holdup in the rod and ball mills. In the ball mill, the holdup is generally lower than that in the rod mill at corresponding feed rates. As is clear from Figure 8, the maximum feed rate to the ball mill is much less than that for the rod mill. The increase of holdup with increasing feed rate probably results from the resistance offered by the grinding media (balls or rods) to the flow of particles through the mills. As a result, an increase in feed rate to the system requires a higher head for material to push itself through the grinding media to reach the discharge end. The reason for the lower holdup in the ball mill compared to that in the rod mill under identical dimensionless conditions is probably due to the difference in the holdup distribution in the two mills. Further studies are needed to explain this phenomenon.
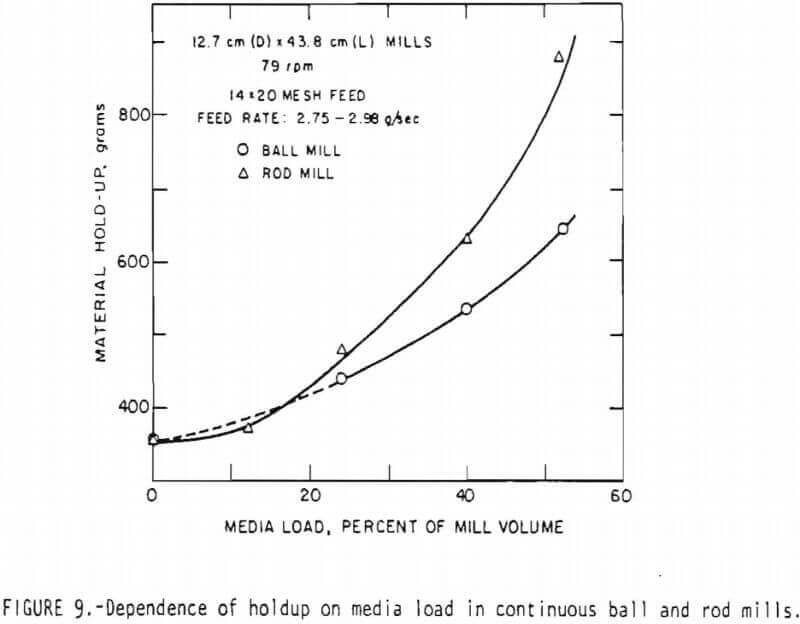
Effect of load of grinding media on holdup: The holdup of material in the mill increases as the media load (balls or rods) increases at the same feed rate. In addition, one can see from the results plotted in Figure 9 that the holdup in the ball mill is lower than the corresponding holdup in the rod mill. The increase in holdup with media load may be attributed to the increased resistance to material flow as the media load is increased. At lower levels of media load, most of the shear zone will be free of the media and the material will experience a relatively small resistance in moving towards the discharge end. Hence, a smaller driving head is required to push material through the mill, resulting in a lower holdup at low media loads. As the media load increases, an increased interaction between the flowing material and the media ensues, resulting in a higher resistance to material transport. This, in turn, requires a higher material head for the material to discharge at the same rate resulting in a higher material holdup.
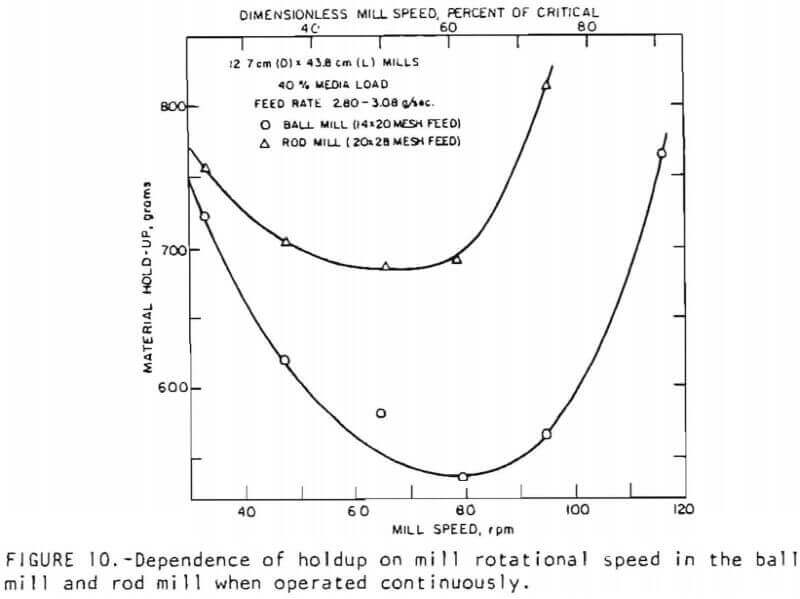
Effect of mill speed on material holdup: Figure 10 shows the material holdup as a function of mill speed for both rod and ball mills. As can be seen from the results given in this figure, the holdup in the ball mill at all speeds is lower than the corresponding holdup in the rod mill under similar operating conditions. This, again, is perhaps related to the differences in the axial holdup profiles in the two systems. The holdup is larger at both low and high mill speeds, passing through a minimum at the intermediate speeds. The holdup is high at low mill speeds because of the high friction to the flow of material as a result of the presence of a thin shear zone, and is high at high mill speeds because the flowing material cataracts and occupies more volume in the mill. In both ball and rod mills, the material holdup is an increasing function of mill speed in the commercial operating range of mill speeds.
Effect of material feed rate on RTD: Figure 11 shows the Peclet number and the dispersion coefficient of the material flowing through the rod mill as a function of material feed rate. The Peclet number increases and the dispersion coefficient decreases with increasing feed rate. Similar trends of Pe and D with variation in feed rate were observed in the ball mill. This behavior for both the mills may be explained by recognizing that, under a fixed media load and mill speed, at low feed rates to the mill the level of

the material surface in the mill is low. This implies that the material in the mill does not completely fill all the voids between the tumbling media. As a result, a large fraction of the flowing material interacts with an “excess” of tumbling media, resulting in a relatively highly dispersed mill discharge. At higher feed rates the holdup of material in the mill increases, filling almost all the voids between the media, and because the material motion is restricted, a low dispersion coefficient results. It was observed that the values of the axial dispersion coefficient are about six times higher in the case of the ball mill than in the case of the rod mill under similar conditions. This appears to be due to the axial shoveling action of material by the relatively unconstrained motion of balls in a ball mill, whereas in a rod mill, the motion of rods is restricted in the axial direction, and, hence, their effect on the axial dispersion of material would be correspondingly smaller. The implications of this significant difference in the material transport characteristics between dry rod and ball mills over the entire range of admissible feed rates cannot be over-emphasized.
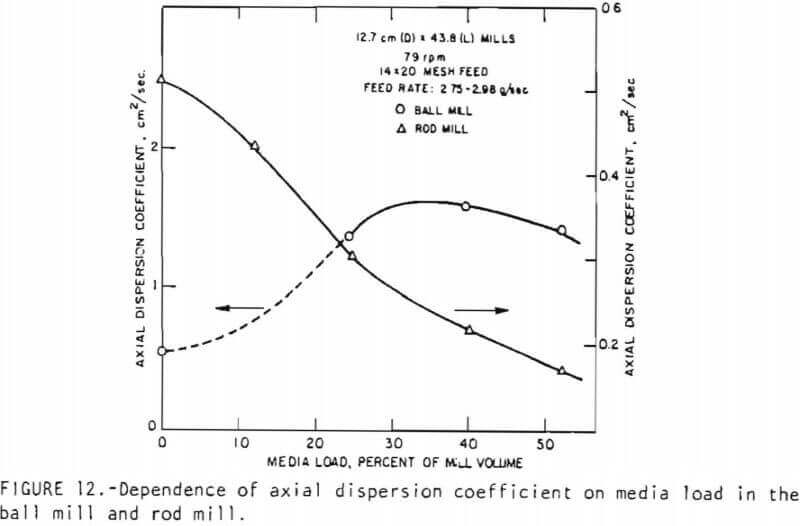
Effect of media load on RTD: The results of this series of experiments are presented in Figure 12 which shows the relation between the dispersion coefficient in both the ball and rod mills as a function of media load expressed as a percent of the mill volume. Clearly, the variation of the dispersion coefficient with media load in the two mills display completely opposite trends. This can be explained in terms of the possible nature of particle/media interactions in the two systems. As already indicated, the axial constraint on the motion of rods considerably limits their ability to disperse the material in the axial direction and this may be the reason the dispersion coefficient is generally low in the presence of rods. In addition, relative to a mill with no tumbling media, the addition of a few rods to the system creates channels of flow between the rods where particle/particle and particle/rod interactions tend to become restricted. In this context, the trajectories of dispersed particles are shortened, and, on the average, the (axial) dispersion of particles with a finite axial component of motion is reduced. With an increased addition of rods to the mill, the flow channels between the rods become smaller and the fraction of material flowing in these restricted sections increases. In turn, this implies that the axial dispersion coefficient decreases with increasing rod load.
In contrast to the effect of media load on dispersion in a rod mill, the addition of balls to a ball mill increases the dispersion coefficient (Figure 12). This is because balls, unlike rods, are free to move axially in a random fashion and increasing the ball load should then result in increased stirring and axial shoveling of particles back and forth, leading to an increase in the dispersion coefficient. Furthermore, it is anticipated that the axial dispersion of particles reflected off the media surface would be much greater in the case of balls. The increase in dispersion coefficient with increasing ball load continues until the particulate bed is almost fully impregnated with balls (at about 40%, ball load). Balls added to the mill beyond this level probably do not participate very much in particle/ball interaction, but rather tend to interfere with the dispersing action of the other balls in the system. This, it is felt, is responsible for the decrease in the dispersion coefficient observed beyond about 40% ball load.
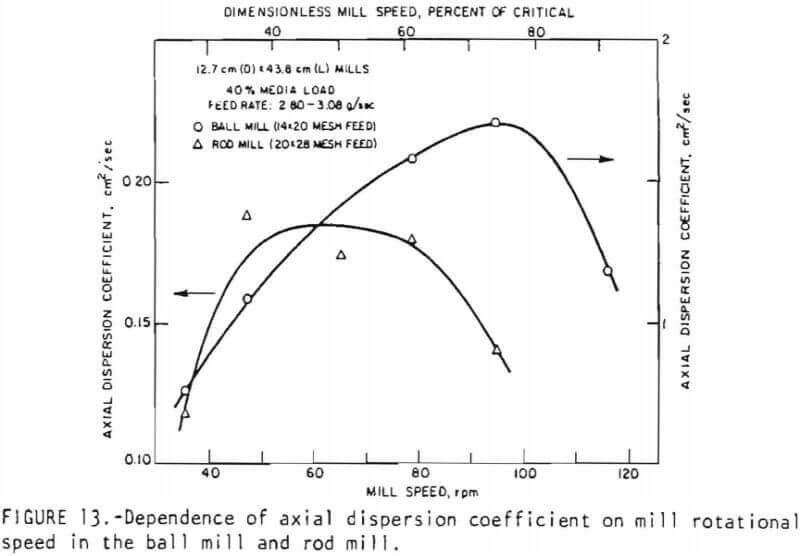
Effect of mill speed on RTD: The effect of mill rotational speed on the axial dispersion coefficient for material flow in ball and rod mills is presented in Figure 13. In both mills, the dispersion coefficient is low in both the lower and higher range of the mill speeds but is higher in between. The lower dispersion coefficient at low mill speeds may be due to the fewer number of particle/particle and particle/media collisions per unit time under these conditions. In the higher range of mill speeds, the onset of cataracting of the media and the material in the empty space of the mill (as discussed in the section on holdup, there this phenomenon is reflected in higher holdup) leads to a reduced frequency of particle/ particle and particle/media interactions, again resulting in a decrease in the dispersion coefficient.
Summary and Conclusions
In this investigation, a detailed experimental analysis of the kinetics of breakage in a rod mill was carried out in the framework of a phenomenological grinding model derived from population balance considerations. The fundamental parameters of this model are the set of breakage rate functions and the set of breakage distribution functions. The dependence of these parameters on feed size and holdup was studied in detail. The results indicated that while the kinetics of the system are inherently nonlinear, they can be adequately represented by first-order behavior for the finer sizes in the mill and for coarser sizes at higher holdup levels. The breakage distribution function was found to be independent of particle holdup and feed size. A predictive scheme for “generating” the set of initial breakage rate functions at any holdup was developed from the experimental data. This scheme has considerable advantages in mill simulation although it has to be used with caution at high levels of particle holdup.
Simulations of the experimental product size distributions were carried out using a linearized grinding model that results from a first-order Taylor’s series expansion of the breakage rate expression. An additional set of parameters, to be called the breakage rate gradient functions, is introduced by the process of linearization and these were evaluated from the experimental data. The model was found to give very good description of batch mill behavior for both mono-sized and distributed feeds. The flexibility of the model to describe the nonlinear breakage kinetics in a rod mill coupled with its good description of batch rod mill behavior makes it very appropriate for its extension to describe continuous rod mill grinding.
Detailed experimental investigations were also conducted to delineate the effect of operating variables on the holdup, mean residence time and residence time distribution of particulate solids flowing through continuous rod mills. For purposes of comparison and in order to clearly identify the transport phenomena involved, identical experiments were conducted in a continuous ball mill. The experimental data were analyzed in the context of the axial dispersion model and through its parameters, namely, the Peclet number and axial dispersion coefficient of the flow regime.
The operating variables investigated include the feed rate to the mill, media load, and mill speed. In both ball and rod mills, the material holdup is an increasing linear function of the feed rate to the mill. In ball mills the mean residence time for material transport is nearly constant with change in the feed rate to the ball mill. However, in rod mills the mean residence time for material transport decreases with increasing feed rate to the rod mill. These results are significant in the context of scaling up the feed rate to a tumbling mill.
Increase in the media load was found to lead to an increase in material holdup, due to the increased resistance to material flow in both systems. The effect of media load on the axial dispersion coefficient in ball and rod mills is very interesting and not intuitively anticipated. While the dispersion coefficient increased with increasing ball charge due to an increased mixing action, it decreased with increasing rod charge. This seemingly paradoxical phenomenon can be explained on the basis of a postulated mechanism of particle/media interaction in the two systems.
The variation of material holdup with mill speed in both ball and rod mills was found to be quite complex, although they exhibit similar trends in a broad sense. Over a range of mill speeds (about 40 – 60 of mill critical speed for rod mills and 50 – 70 : of mill critical speed for ball mills), the holdup is approximately constant but at rotational speeds above or below this range, the holdup increases sharply. With increasing mill speed, the axial dispersion coefficient displayed a trend opposite to that of the holdup. This was explained on the basis of the anticipated frequency of particle/particle collisions at various mill speeds.
Particulate transport through rod mills has, in the few instances in the past, been assumed to be similar to that through ball mills. The present study has brought out the fundamental differences that exist between particulate flow through these systems. It appears that rod mills operate with considerably different material transport characteristics compared to ball mills under similar conditions, and that one may not, in general, assume material flow through these systems to be similar. A very useful general result is that over the entire range of investigation, the material holdup and Peclet number of the flow regime in the rod mill are higher than the corresponding values in the ball mill under identical dimensionless operating conditions. The importance of the material holdup in determining the breakage kinetics in a grinding mill is well established. Everything else being equal, a higher Peclet number for material transport implies a narrower size distribution in the mill discharge. The narrow size distribution observed in industrial rod mill products has generally been related to the breakage kinetics in these mills, but it is clear from the present investigation that material transport in these mills is perhaps an equally important factor, too.
