Table of Contents
A technique is presented for the economic selection of a slurry pipeline with the aid of a computer. Mathematical models for the flows of homogeneous slurries are utilized. Only the pipeline and its prime movers are considered.
Slurry flow properties are first obtained from rheology and/or pipeline data measurements. A rheological model is then selected for the slurry. It must be emphasized that the accuracy of the method is greatly affected by the accuracy of the slurry flow-property data.
General Explanation
With the surge of growth that slurry pipelining is experiencing, more and more technical and economic evaluations are being conducted to determine the feasibility of pipeline transportation of mineral commodities. These evaluations are frequently based on data which are less precise than those associated with the more conventional materials handling methods, and this uncertainty frequently leads to the rejection of the slurry pipeline concept.
Techniques similar to the one proposed in this paper have been used for the design of oil and gas pipelines. Recognizing the complexity of slurry flow, it should still be possible to develop a similar tool for the flow of slurries in pipes. Skelland has presented an equation for Newtonian and non-Newtonian liquids which gives a total annual cost per foot of pipe length. The equation includes the pumping cost and the pipe cost, but excludes the cost of the pumps and motors. The method presented herein, equally valid for both Newtonian and non-Newtonian liquids, includes the cost of the prime movers in determining the optimum economic pipe diameter and then computes the necessary velocity from the continuity equation to deliver the required throughput.
Theory
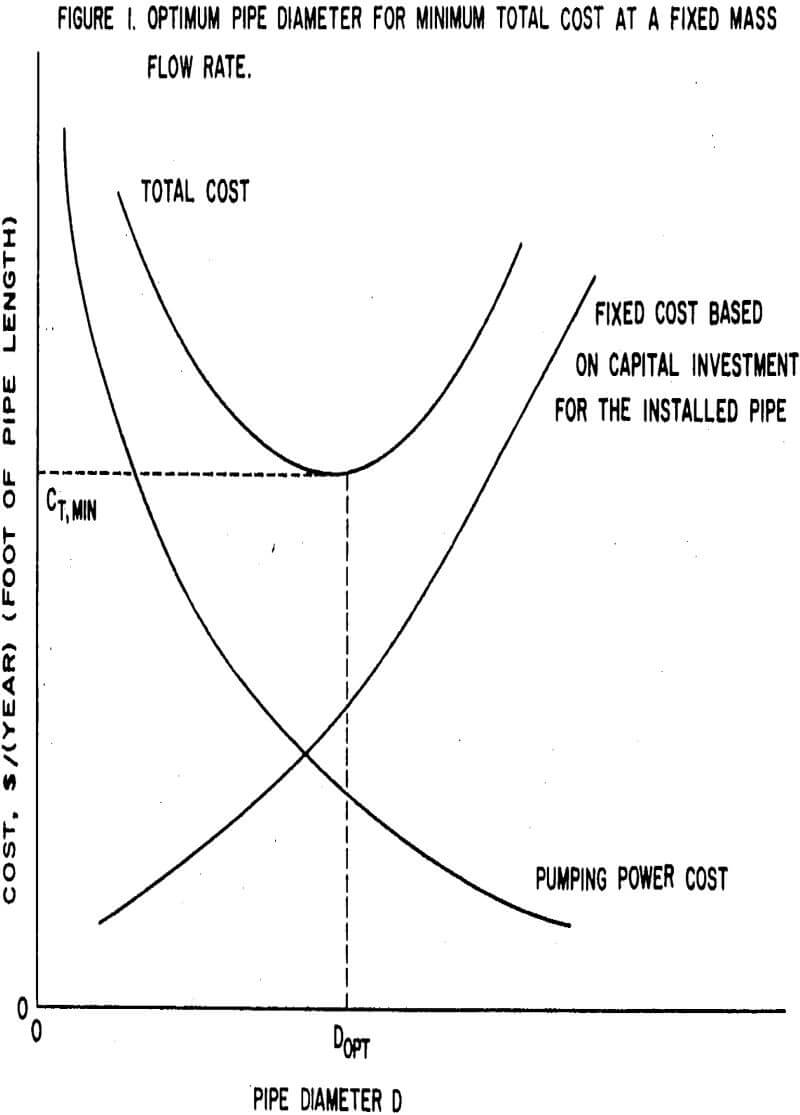
For any given set of flow conditions, the use of an increased pipe diameter will cause an increase in the fixed costs (capital costs) for the piping system and a decrease in the pumping costs (operating costs). Therefore, an optimum economic pipe diameter must exist. The value of this optimum diameter can be determined by combining the principles of fluid dynamics with cost considerations. The optimum economic pipe diameter is found at the point where the sum of pumping costs and fixed costs based on the cost of the piping system is a minimum.
In accordance with the exceptions noted earlier, the total cost expression will comprise standard equipment only. Unique features that vary from one situation to another will not be considered. Thus, the annual total cost expression (C Total) for pipeline transportation of mineral commodities can be expressed as follows:
C Total = C Pumping + C Pipe + C Pump + C Motor………………………………….(1)
The first term on the right-hand side of Eq. (1) represents the operating cost and the last three terms represent the capital and maintenance costs of the pipe, pumps and motors, respectively.
The complexity of the total cost expression is a function of the flow regime and the rheological model selected to describe the slurry. According to Govier and Aziz, many non-Newtonian homogeneous slurries can be defined by the general mathematical model τ-τy = Ky. The generalized model reduces to simpler expressions for other rheological models as follows:
- Newtonian fluids τ = uγ; (n = 1.0, K = µ)
- Bingham plastic slurries τ – τy = Kγ; (n = 1.0)
- Pseudoplastic slurries τ = Kγn
where: τ is the slurry shear stress
τy is the slurry yield stress
µ is the slurry dynamic viscosity
γ is the slurry shear rate
K is the slurry consistency index
n is the slurry flow behavior index
Case Study
The material handling problem stated that a fine limestone with specific gravity of 2. 661 and concentration by weight of 58.3% was to be transported at a rate of 200 dry short tons per hour, in the form of a slurry, by a pipeline over a distance of 11.74 miles. The rheological model assumed for the slurry was pseudoplastic.
A wide range of pipe diameters (2-, 4-, 6-, 8-, 10-, 12-, 14-and 16-inch) was specified for the first computer run. The purpose of this run was to narrow the range of pipe diameters for the final study.
A closer range of pipe diameters (4-, 5-, 6-, 7-, 8-, 9-, 10-, and 11-inch) was specified for the second computer run. From this run, it will be seen that a minimum cost per ton mile is obtained with a 7-inch pipe, and that a pump is still not required.

