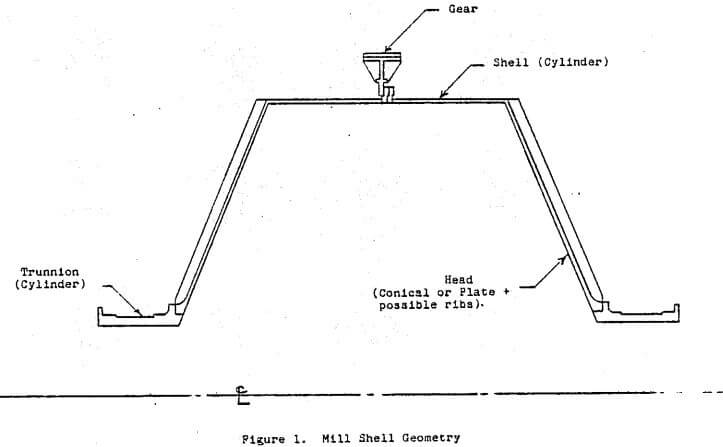
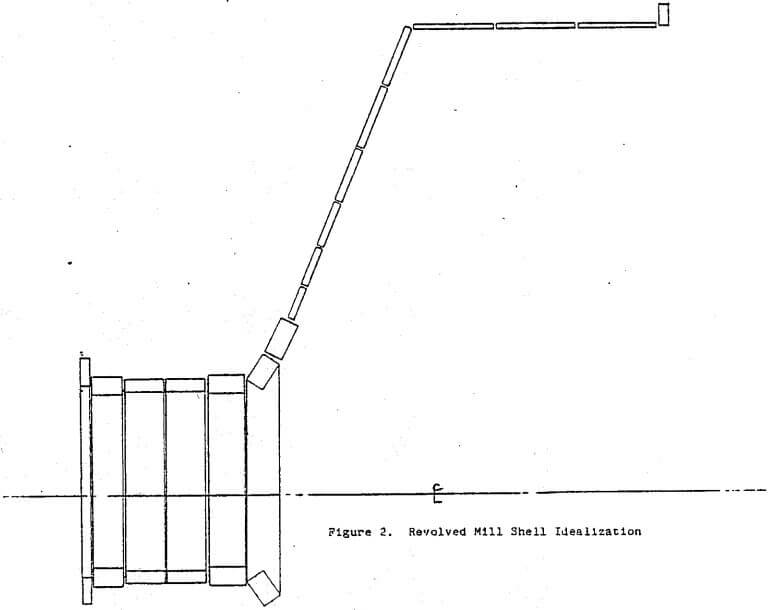
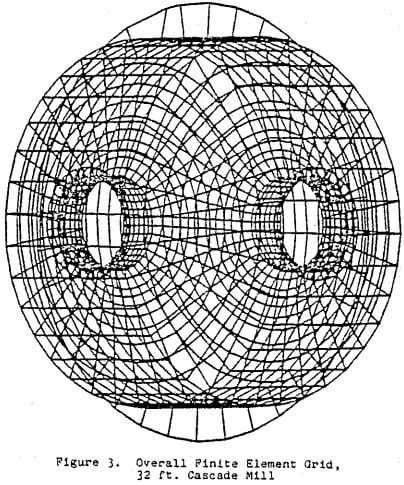
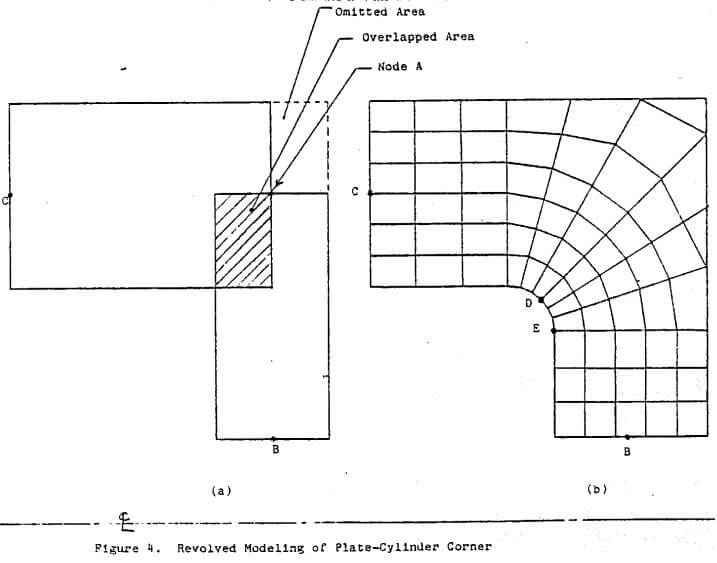
Table of Contents
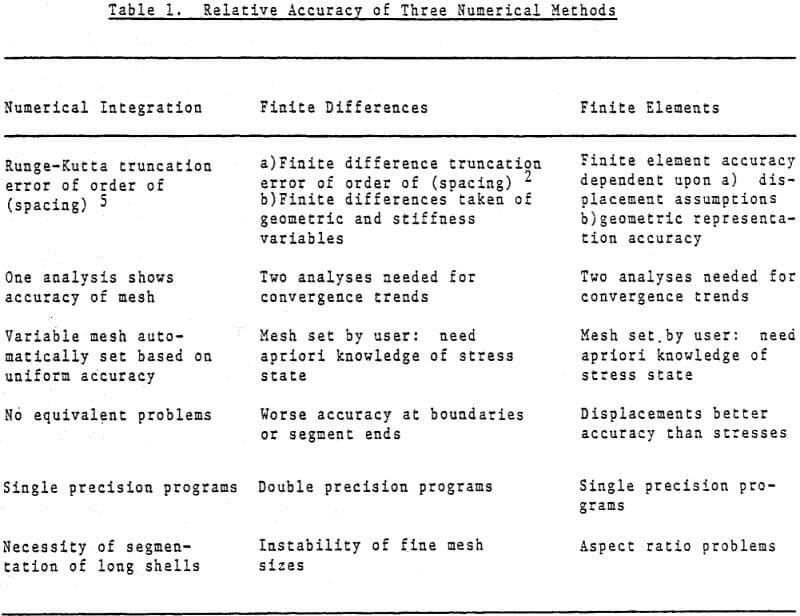
Accurate modeling of structures by finite elements requires not only that the user estimate the load paths, and areas of stress concentrations or rapid variations, in a structure, but also that he realize the modeling idiosyncracies of each element he is working with. He needs to know limitations in displacement function assumptions, aspect ratios, angles, the effects of mixing triangles and quadrilaterals, etc. The only way much of this expertise can be truly assimilated is through detailed familiarity with the element derivations, wherein limitations become obvious. Occasionally the program developers make the user’s problem even more complex by retaining rather than replacing elements which have proved defective in modeling in further program updates. Thus, often the choice for the user is basic: either obtain a detailed course in finite element modeling (not just a short seminar), and study in detail the theory manuals of each general purpose program to be used (often compiling his own documentation of pitfalls and element verifications), or turn to the use of simpler specialty programs. The latter path will be more difficult, since it will require the knowledge of a number of programs, each with its specialized area of application.
Stress Evaluation
Once the mill analyst is able to predict the stresses in his structure to within acceptable limits, he is further faced with the task of evaluating the acceptability of this stress condition. As noted earlier the mill shell design criteria is long-life fatigue, i.e., the mill operation life is expected to be greater than 20 years continuous running. Therefore, the analyst’s stress acceptance criteria must be based on long-life fatigue crack initiation and growth.
This may be achieved in one of two methods, either through the use of stress versus life curves, or through the application of newer fracture mechanics principles.

Fatigue Life Diagrams
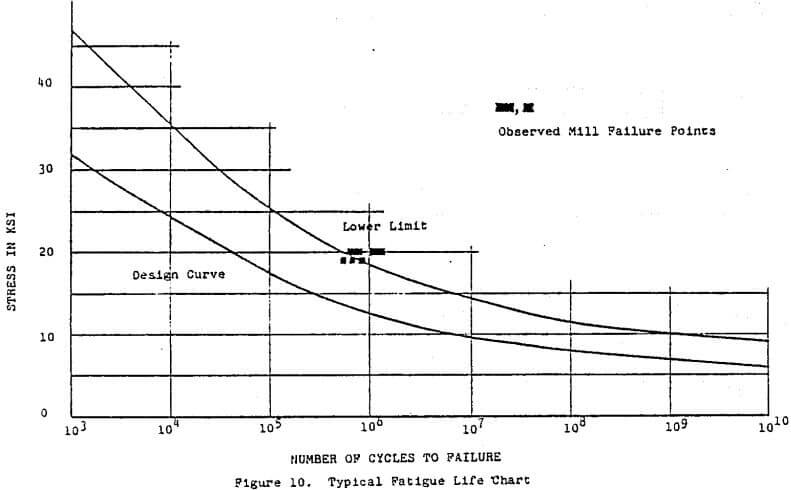
Fatigue life curves or S-N diagrams are the standard charts used in fatigue design. Examples of such diagrams are available in the Boiler and Pressure Vessel Code of ASME or the AWS Structural Welding Code. In these charts, as for example in Figure 10, stress amplitude is ploted versus number of cycles to failure.
For most mill operation the lifetime cycles for design conditions are in the range 2 to 5 x 10 8 cycles. This is a rather high cycle fatigue life requirement. It is just this high number of required cycles that make the creation of the life curves difficult. Both the ASME and AWS codes essentially end at 10 6 cycles. This is due to the fact that test data above 10 6 cycles require long running of fatigue machines and are very expensive to gather. However, horizontal asymptotes (fatigue limits) are not necessarily acceptable beyond this range and some type of extrapolation formulae must be utilized.
In order to obtain a satisfactory S-N curve for mill design the following.procedures may be utilized. First all fatigue data on the steel of interest should be obtained and a lower bound curve drawn below all the experimental points. The lowest experimental points can be used numerically in extrapolation formulae to a number of cycles such as 10 9 or 10 10. One such formula presently being recommended to the ASME codes is:
![]()
where alternating strain (ea) is expressed as a function of cycles (N) greater than 10 6. This procedure would result in the lower limit curve of Figure 10. Any known failures with the steal as used in mill structures should be plotted for comparison (see Figure 10). This would serve both as a check on the source of the steal data, as well as on the stress calculations used for the mill.
Upon obtaining a lower limit curve as described above, one should evaluate the quantity of data that was used to obtain the curve. The amount of data points available determine the quality of the lower limit curve, i.e., if there were ten points the lower limit curve is a 10 percentile curve, whereas with 100 points it would be a 1 percentile curve. Upon evaluating the data used, the analyst can then decide how trustworthy the lower limit curve actually is, and what factor of safety may be necessary to obtain the acceptable design curve (Figure 10). The design curve is usually some factor (<1) times the lower limit curve.
In utilizing and creating S-N design curves in the above fashion the following items should be considered:
- The stress range design curves should either be created for several stress ratios (R=max. compression stress/ max. tensile stress), or separate curves for maximum tensile stress (as a function of R.) should be used. This is due to the fact that mean stress can be expected to have a more significant effect on long life fatigue where the overall stresses remain elastic.
- The S-N design curves need to be created for parent metal and the several types of welds which may be used on the mill structure. In creating weld S-N, curves, the use of nominal stress is recommended due to unknown stress raisers inherent in different quality weldments. Note also that the way a welded joint carries load may be just as important for fatigue life as the type of weld being used.
- Separata S-N design curves will be required for any cast heads or trunnions.
Fracture Mechanics Methods
Fracture mechanics methods may also be used to obtain fatigue design criteria for mill structures. While these methods are more sophisticated, and better recognize the micromechanics of fatigue cracking than the previously described methods, they are harder to apply at present to more practical structures like mill shells with their attendant weldments in critical areas. They are also dependent on most accurate predictions of local stresses.
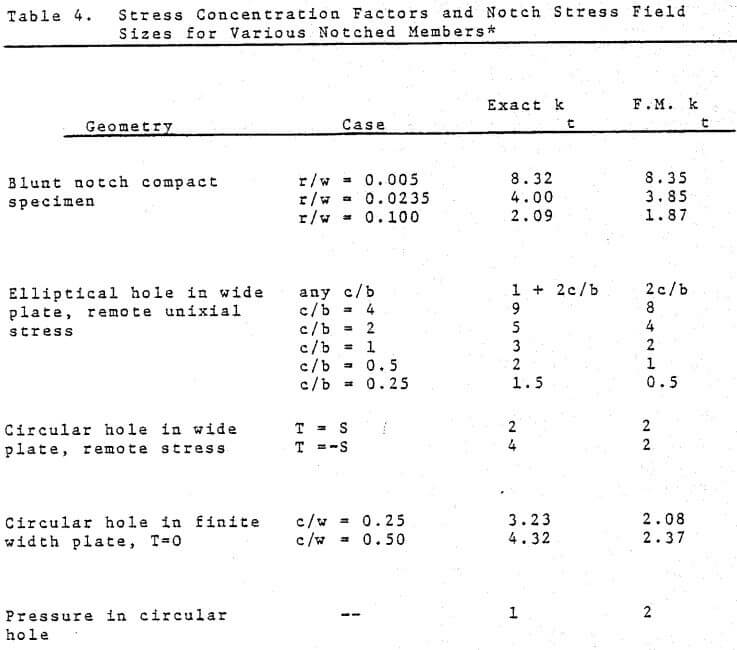
These predictions of local stresses at sharp discontinuities in welds or notches are usually obtained on the basis of using elastic stress concentration factors, kt, from the fracture mechanics calculations. However, these are not always accurate as demonstrated in the collected data of Table 4 (see Reference 7) where exact finite element solutions are compared with the values obtained by fracture mechanics formulae. Where fracture mechanics estimates of kt are in-accurate, difficulties may be expected in correlating related fatigue data predicted by these methods. Thus it is advisable to obtain the kt factors by means of small local finite element models. However, the difficulty arises in accurately describing for finite element modeling a discontinuity left by a weld pass or a shrink in a casting, each of which is only detectable by ultrasonics or radiography, respectively. Therefore, the application of such methods in non-precision structures like mills is indeed difficult and very approximate at the present time.
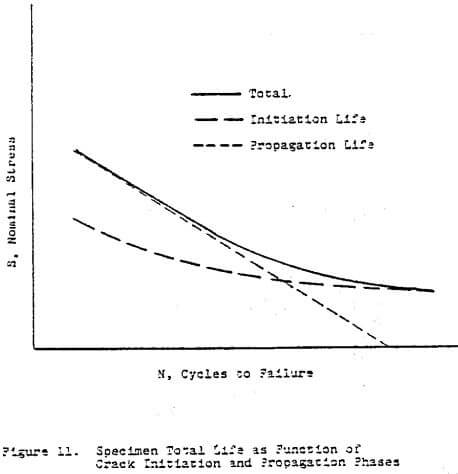
In addition, it should be recalled that mill design criteria requires long-life fatigue at many cycles. As shown schematically in Figure 11, fatigue life can be characterized as being dominated by a crack initiation phase or a crack propagation phase. For shorter lives, notch plasticity effects and crack propagation dominate the life predictions.
For high-cycle fatigue life, however, at stresses substantially below yield, most of the time is spent in the crack initiation phase. Thus design by fracture mechanics principles is more or less comprised of seeking fatigue threshold stress intensity factors, and thence, values of stress at which specific cracks will not propagate at all. These threshold values are again hard to come by since they require long and expensive fatigue testing.
It can therefore be seen that fracture mechanics as a means of formulating a, design criteria for mill shells is still somewhat of an art. Once a crack is found in a .mill in the field, however, with a well defined geometry and associated stress, linear elastic fracture mechanics serves as an excellent tool to predict crack growth and potential critical failure.