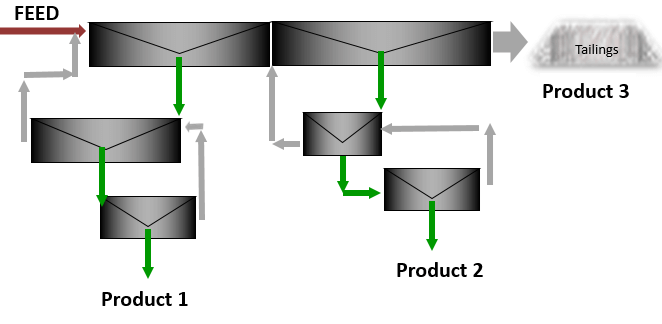
Frequently, a concentrator will mill a complex ore requiring the production of two separate concentrates, each of which is enriched in a different metal or valuable mineral, plus a final tailing acceptably low in both constituents. Formulas have been developed which use the feed tonnage and assays of the two recovered values to obtain the ratios of concentration, the weights of the three products of separation, and the recoveries of the values in their respective concentrates. For illustrative purposes data from a copper-zinc separation is assumed.
The ratios of concentration, Kcu and K/n are those for the copper and zinc concentrates, respectively, with Rcu and R/n the percentage recoveries of the metals in their corresponding concentrates.
The three product solution illustrated above can be somewhat simplified by taking an intermediate tailings sample between the two stages of concentration; i.e., a copper tail (zinc feed) sample in the previous example.
Cytec
In the 2000 page Handbook of Mineral Dressing by A. F. Taggart, the subject of material or metallurgical balances is covered in only six pages of eve-straining type, although Taggart’s work was compiled before 1945, and there has been significant progress since then in most areas of mineral processing, the practicing metallurgist’s approach to metallurgical balances remains exactly the same as described in those six pages.
There are several portions of Taggart’s text appropriate to introduce the subject of this paper which I would like to quote:
“Milling Calculations. Computations of performance in milling are complicated by the fact that it is a continuous rather than a batch operation, that the quantities of solid materials handled are large and usually mixed with water, hence difficult or impossible to weigh. Fortunately it is possible to determine many facts concerning performance without knowing weights, if the value of various constituents is known in some common unit, e.g., the content of some particular metal or mineral, or of water, or some ingredient soluble therein, or of particles of a particular size or falling within some particular size range, or the like.”
Taggart then proceeded to derive the formulas for calculating weight splits and mineral recoveries from assay, size distribution or water to solids ratio data for the two product, three product and n-product processing situations, and concluded with the following comments:
“Limitations of multiproduct formulas. The formulas above given are theoretically correct but the accuracy of the answers that they give is, of course, wholly dependent upon the accuracy of the sampling and assaying. The formulas for two-product treatment are not particularly sensitive to small errors in data or calculation, hence recovery and weight of concentrate should check smelter returns (or their equivalent). If they do not check, mill operation should be examined for spills, losses, hold-backs as in tanks, etc. and shipping and smelter sampling should be carefully scrutinized.
The formulas for three or more products are more sensitive to small errors both in data and calculation, especially when one of the products is of relatively small weight and low assay.”
The data available today from mineral processing operations is still largely in the form of assays, size distributions and percent solids information obtained on samples extracted from the process. However, the expensive and tedious wet chemical or fire assaying techniques of yesterday are gradually being replaced by automated instrumental techniques which frequently provide multi-component assays for each sample and in fact sometimes are incorporated “on stream” in the actual mineral processing operation. Percent solids measurements are also made routinely “on stream” by gamma gauges or other instruments, and “on stream” size distribution measuring devices are beginning to gain acceptance.
Sampling devices themselves have seen considerable improvement in the past thirty years, while another worthwhile and important advance has come in the ability to measure process flows of slurries and solids in slurries with magnetic flowmeters or other flow sensors in conjunction with gamma gauges.
This then results in much more useful data being routinely available to the plant metallurgist for determining what is happening (“on stream”), or has happened in the process. In addition the advent of the computer and more recently the inexpensive programmable calculator to take the place of the slide rule has put much more calculating power in the hands of the metallurgist or technician for evaluating the data at hand.
The only ingredients required to complete the recipe for greatly improved metallurgical calculations are an understanding of the techniques required to use these data and calculating powers wisely and a recognition of the advantages of so doing. That then is the purpose of this paper: (1) to describe some of the basic concepts and techniques required to use the available data and (2) to demonstrate the practical benefits to be derived from applying these techniques.