A comprehensive analysis of the entire range of related studies would require a lengthy discussion. Instead, this paper will focus only on the work of Visman (1962, 1969), because his work is part of the current ASTM D2234 standard on coal sampling (American Society for Testing and Materials, 1985). Visman’s work attempts to empirically determine a formula for sampling error. Visman has called this work “a general sampling theory“. The theory is intended for both stationary and moving streams of heterogeneous material. Two sets of increments are taken: one set of small increments and one set of large increments. Each increment is analyzed separately. Two constants A and B are estimated and used in the empirical formula for the variance between increments of a given size W:
σ²I(w) = A/W + (1 – 1/W)B.
Here A represents the “random variance” and B the “segregation variance”. Visman uses a “sampling board” to simulate sampling from populations with various degrees of segregation.
Duncan (1971) shows that this empirical formula can be approximately deduced theoretically, and further that
B = pA
where p is the correlation between increments of the same size. Duncan (1971) points out that the formula is only strictly valid for random sampling, while Visman used systematic sampling in the sampling board experiments.
Duncan (1971) also questions the assumption that p is the same for different increment sizes. Duncan expects p to decrease as the increment size increases. Duncan’s expectation and Visman’s assumption are not in agreement with the geostatisical concept of regularization. Regularization concerns the change in variance γ between increments (cores, channel samples, etc.) as the (support) size of the increment changes. As a result of the central limit effect, as the increment size increases, the variance decreases. Typically, the decrease from a smaller support size W1 to a larger support size W2 can be modeled approximately (but adequately) by subtracting a constant k > 0 (based on the variance within the support) from the semi-variogram γ1 for the smaller support as shown in Fig. 1. (This approximation is not valid for distances d < W2.) This approximation is in good agreement with sample data.
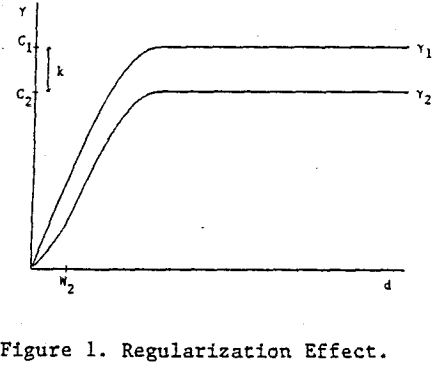
The correlation between larger increments can be shown to be greater than for smaller increments. For example, if the semi-variogram for the smaller increments has a sill C1 > 0, the correlation p1 for the smaller increments is
p1 = 1 – γ1/C1
The sill for the larger increments C2 > 0 is given by
C2 = C1 – k
and the correlation for larger increments p2 is given by
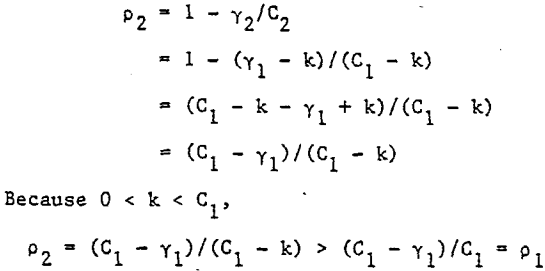
Therefore, the correlation between larger increments will be greater than the correlation between smaller increments.
In Visman’s approach, the variance of the set of small increments and the variance of the set of large increments are calculated. This is equivalent to (an inefficient) estimation of the sills C1 and C2. Thus, Visman’s approach makes another untenable assumption: the variance between increments of the same size is constant and does not decrease as the distance between increments decreases. The two assumptions that Visman makes can be eliminated by a more efficient analysis of the data. The semi-variogram for each set of increments should be calculated. In the geostatistical approach, p is not assumed constant and the change in variance between increments of a constant size is directly estimated from the data. Additionally, the geostatistical approach requires only half as much data, because the appropriate semi-variogram for a different increment size can be determined using regularization.
Several points should be noted concerning Visman’s general theory of sampling:
- The “general” theory is only concerned with the (admittedly very important) problem of sample precision.
- The work is almost entirely empirical. Even simple attempts at deriving mathematically rigorous results were not made.
- An attempt is made to quantify segregation.
- Unnecessary over-simplifications were made that invalidate the method.

