Table of Contents
WHIM is the short acronym for Wet High Intensity Magnetic Separation. At present, most U.S. iron raw materials are produced from magnetic taconites, which are ground to a nominal minus 270 mesh (53 micrometers), beneficiated by wet low-intensity magnetic separation, and pelletized. The taconite ore bodies generally contain 19 to 25 percent magnetic iron, defined as iron occurring in the mineral magnetite. Iron occurring in other minerals, such as iron silicates, siderite, and hematite, is generally lost in the tailings.
The iron-bearing materials intermediate in properties between the high-grade enriched iron ore deposits and the parent taconite are the oxidized taconites. The magnetite has been oxidized to hematite, and the iron silicates and siderite have been converted to goethite, a hydrated iron oxide. There may be some iron enrichment due to natural leaching of silica and migration and precipitation of iron ions in secondary iron oxide layers. Oxidized taconite is also called nonmagnetic taconite to distinguish it from the unaltered magnetic taconite. The western part of Minnesota’s Mesabi Range contains in excess of 10 billion tons of oxidized taconite containing 30 to 40 percent iron. Typically, oxidized taconite surrounds and underlies an exhausted natural ore pit, while underlying the oxidized taconite is the parent taconite. In open pit mining of taconite, oxidized taconite is often removed as waste material. In some cases, oxidized taconite is being stockpiled for future use, in other cases, it is discarded with the overburden. The development of an economical method for beneficiating oxidized taconites would utilize a current waste material and convert the oxidized taconite from an iron ore resource to a reserve.
Compare Magnetic Separation Methods
The Bureau of Mines is investigating the following three most promising technologies for the beneficiation of oxidized taconites:
- Reduction roasting of the hematite and goethite to magnetite, followed by low-intensity magnetic separation and flotation.
- Selective flocculation of the iron-bearing minerals, followed by froth flotation.
- Wet high-intensity magnetic (WHIM) separation, either alone or in combination with selective flocculation and froth flotation.
To obtain objective technological and economic analyses of these beneficiation processes, all three are being evaluated on a pilot plant scale using the same samples.
In the reduction roasting process, the hematite and goethite in the ore are converted to magnetite by heating in a reducing atmosphere at approximately 800° C. Although the first experimental plant was built on the Mesabi Range in 1934, the process has not been used commercially. The high operating cost of the energy consumed in roasting is partially compensated by reduced grinding costs and by energy returned in the conversion of magnetite to hematite during pellet induration. The capital cost, which is also high, would be reduced if roasted ore were processed in an existing magnetic separation plant. However, processing of reduction-roasted ore in a conventional taconite plant would require some modifications, because artificial magnetite has a higher remanence and coercivity than natural magnetite. After exposure to a magnetic field, very strong magnetite floccules, which entrain gangue particles, are formed. Demagnetization requires special high-frequency coils. Pilot plant results recently obtained by the Bureau of Mines show that the silica content of the artificial magnetite concentrate can be reduced to less than 5 percent while iron recovery is maintained at 80 percent by including a froth flotation step after the final magnetic separation stage.
Highly metamorphosed schistose iron ore from the Marquette range on Michigan’s Upper Peninsula has been successfully treated by froth flotation since 1956. The hematite in this ore occurs in the form of specularite, which is more easily beneficiated than the red or dull black hematite typical of oxidized taconites. The development of selective flocculation by the Bureau of Mines and research by the Cleveland-Cliffs Iron Co. made flotation a feasible beneficiation method for the bulk of the Lake Superior region’s oxidized taconite resources. The research resulted in the opening of the Tilden plant (Marquette range, Michigan), which has a capacity of 4 million tons of pellets per year; long-term plans call for tripling the plant’s capacity. Mesabi Range oxidized taconites can also be beneficiated by selective flocculation-flotation; however, the much greater content of goethite in the Minnesota oxidized taconites, compared with the Tilden ore, makes it more difficult to maintain high iron recovery. A typical flowsheet for Mesabi Range oxidized taconite is shown in figure 1.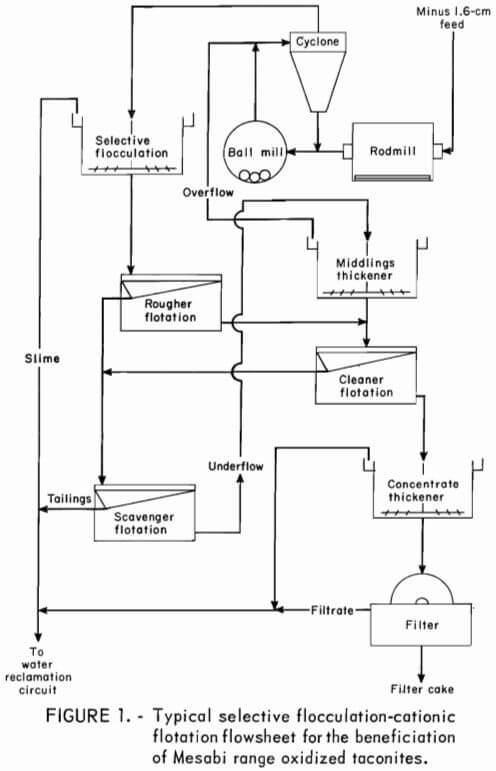
The application of WHIM separation to the beneficiation of oxidized taconites received impetus from innovative separator designs developed by G. H. Jones and J. H. Carpenter in the early 1960’s. Beginning in 1964, application of WHIM separation to Mesabi and Marquette range iron ores was tested on the pilot plant scale at the Mines Experiment Station (now the Mineral Resources Research Center) of the University of Minnesota. The flowsheet developed involved WHIM separation on rodmill-ground ore to remove coarse quartz and primary slimes amounting to 20 to 30 percent of the feed weight. The preconcentrate obtained was reground in a ball mill, and the final concentrate was produced by flotation. The flowsheet development was influenced by the fact that the WHIM separators available used soft-iron spheres as a matrix and were not capable of selectively recovering the iron oxides present in particles finer than 500 mesh (25 micrometers). After flotation, overall iron recoveries ranged from 72 to 78 percent. In 1974, Kelland and Maxwell demonstrated that a continuous pilot plant WHIM separator with a matrix designed to produce high field gradients could be used to preconcentrate oxidized taconite ground to 90 percent passing 400 mesh (37 micrometers) before flotation. When a single-stage operation employing a 10-cm length of stainless steel wool matrix was used, preconcentrates containing 49 to 54 percent iron, with iron recoveries ranging from 68 to 79 percent, were obtained.
On the basis of direct operating costs, exclusive of amortization, WHIM separation, either alone or in combination with flotation, is less costly than either reduction roasting or selective flocculation-flotation. The cost advantages of WHIM separation over flotation are decreased reagent, grinding, and water treatment costs. For commercial-scale machines, the energy required to energize the electromagnets, typically in the range of 1 to 5 kwhr/ton of ore treated per pass, is small compared with the 30 kwhr/ton required for grinding. From the standpoint of capital costs, WHIM separation is significantly more expensive than flotation but probably less expensive than reduction roasting. Since WHIM separation is a relatively new and untried technology for the processing of oxidized taconites, high investment expense is a significant barrier to its application. Even at the research and development level, progress has been hindered by the high cost of effective pilot-scale machines. To minimize capital costs, the number of magnetic separation stages must be kept to a minimum.
Wet High-Intensity Magnetic Separation Results
Tests were conducted on a bulk sample of oxidized taconite from the western Mesabi Range. The sample represents ½ to 1 billion tons of crude ore.
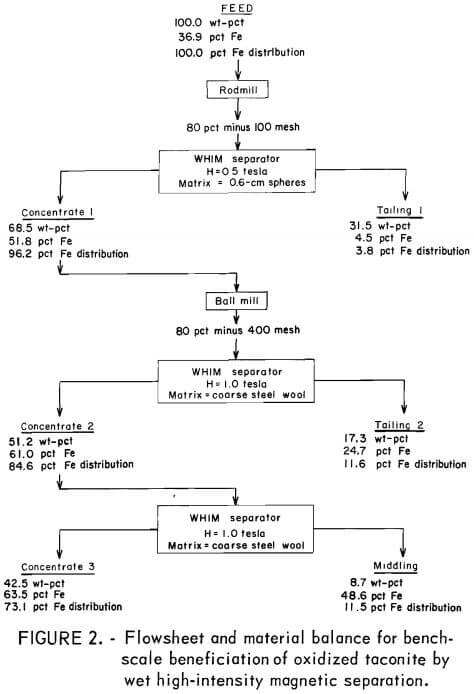The possibility of beneficiating the sample by WHIM separation alone was evaluated in the laboratory on 1-kg samples (fig. 2). A sample of rodmill discharge was separated in an Eriez Model L-4 WHIM separator with a 20-cm-deep matrix of 0.6-cm iron spheres and a 0.5-tesla applied field. A coarse tailing containing 31.5 percent of the feed weight, but only 3.8 percent of the iron in the feed, was obtained. To achieve sufficient liberation of the ore, the preconcentrate was reground to 80 percent passing 400 mesh (37 micrometers). Separation of the reground material was carried out with a matrix of coarse stainless steel wool and a 1.0-tesla applied field. Two stages of separation produced a finisher concentrate containing 63.5 percent Fe and 5.5 percent SiO2 with an accompanying iron recovery of 73 percent.
The laboratory results have not been duplicated in the pilot plant. The WHIM separators available for this research have not performed satisfactorily in continuous operation on rodmill discharge; the separators have either given much lower iron recovery than expected from laboratory tests or have shown a tendency to plug up during extended runs. (Design criteria for avoiding these difficulties are discussed in a subsequent section.)
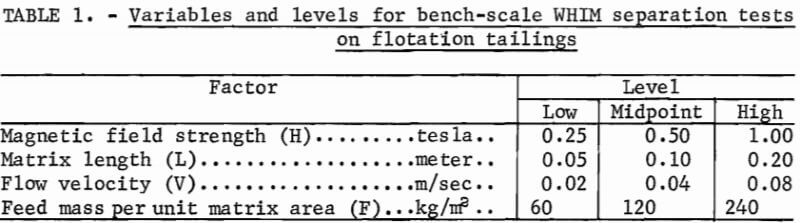
The Bureau of Mines most successful application of WHIM separation on a pilot plant scale has been as a method of increasing iron recovery in the selective flocculation-flotation process. The unit operations of figure 3 were used in conjunction with the flowsheet of figure 1. The WHIM separator recovered iron values from the scavenger flotation tailings. The magnetic concentrate, after thickening, was returned to the scavenger flotation cells. During a continuous 48-hour pilot plant test in which the magnetic concentrate was recycled to the flotation circuit, the iron recovered in the cleaner flotation concentrate was increased by 2 percent with no adverse effect on concentrate grade. Average metallurgical results for a 48-hour period during which flotation was producing a low-iron tailing are shown in figure 4. Preliminary results from 6-hour pilot plant tests on higher grade flotation tailings have indicated that up to 10 percentage units of iron can be recovered by WHIM scavenging. The MEA-Sala Carousel magnetic separator used was operated at 0.6 tesla with flow through the 9-cm matrix of coarse stainless steel wool controlled by gravity.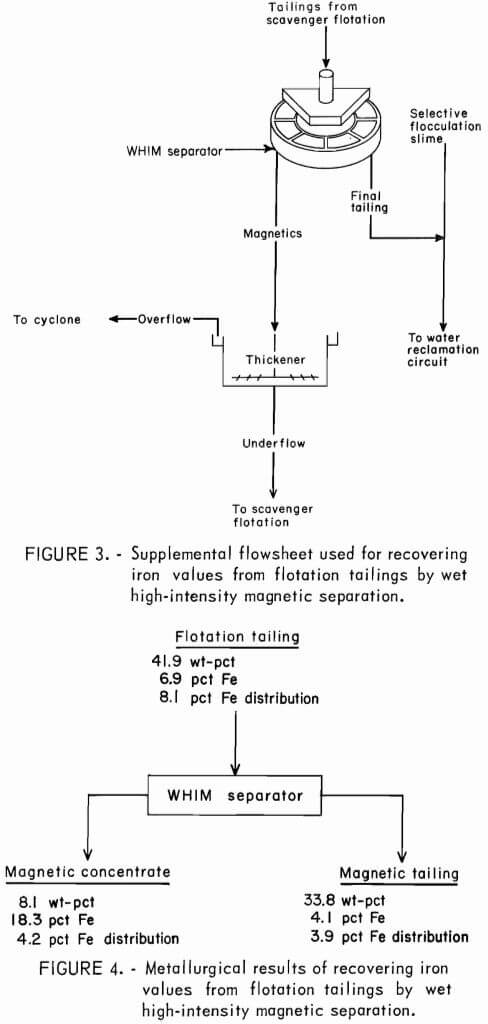
The flotation process used was the cationic flotation of the gangue. To improve the concentrate grade, more amine collector is added to ensure flotation of coarse gangue particles. However, the added collector can also cause flotation of fine iron oxides, leading to a decrease in recovery. By providing a means of recovering the fine iron, magnetic scavenging allows positive control of the final concentrate grade while minimizing loss of iron values in the final process tailing. An effective means of controlling iron recovery while maintaining close concentrate grade control is significant in treating an ore as variable in its characteristics as oxidized taconite.
Mathematical Models to Optimize Magnetic Separator Design
Because alternative processing methods and alternative sources of ore exist, WHIM separation will be commercially applied to oxidized taconites only if it is cost competitive. The key to minimizing costs is to optimize the separator design for a particular application. A rational optimization procedure requires a mathematical model of separator performance as a function of the basic design and operating parameters.
Most existing models of WHIM separation can be classified as highly theoretical or purely empirical. During the past few years, there has been much interest in the development of theoretical models of WHIM separation based on particle trajectory calculations. Recent computer-based models have shown some degree of correspondence with experimental results after the introduction of two adjustable parameters for each particle size. Application of a theoretical model to a practical optimization problem would require a very extensive ore characterization study followed by systematic testwork to determine the adjustable parameters. The calculations involved in finding an optimum separator design might be too cumbersome for practical design purposes, even when performed on a large electronic computer. Several empirical models relating WHIM separator performance to design and operating parameters have been published. Because the amount of testwork required expands rapidly with the inclusion of each additional independent variable, empirical models are rarely developed to the degree of generality required for optimizing separator design. Since neither purely theoretical nor purely empirical models are well suited to design optimization procedures, a significant opportunity for advancing WHIM technology lies in the development of phenomenological models, which combine the most useful features of the theoretical and empirical approaches. Typically, in this compromise approach, theoretical analysis is used to derive or suggest reasonable, uncomplicated forms of the descriptive equations, but statistical curve-fitting techniques are used to find the parameters that fit the data to the equations. With the proper form of the descriptive equations, the required number of adjustable parameters and the testwork required to establish their values can be decreased to a minimum. The following example will illustrate the development and use of a simple phenomenological model.
Concurrently with a 5-day pilot plant test during which magnetic scavenging was tested, samples of the flotation tailings were evaluated in bench-scale WHIM separation tests under controlled conditions. Over the 5-day period, a 24 factorial experiment was run. The effect of daily variations in the tailings was assessed by conducting two midpoint tests each day. The variables and levels used in the tests are shown in table 1. The dependent variable of most interest, the fractional iron recovery, was shown to be independent of the iron content of the tailings, which varied from day to day. Equations developed by Oberteuffer and Watson suggested the following phenomenological equation:
The properties of the feed, such as its particle size distribution, did not vary significantly; therefore, the model was not complicated unnecessarily by including the effect of particle size on recovery. The feed characteristics have a strong effect on the parameter α and a lesser effect on the other parameters.
The five unknown parameters in equation 1 can be determined by linear regression techniques if the equation is transformed to
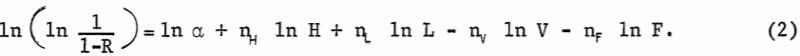
To obtain accurate values of the parameters, weighting factors determined by the variance of the transformed dependent variable should be used in the regression calculation. It is of interest to compare equation 1 with the strictly empirical equation of Dobby and Finch, in which recovery is expressed as a linear function of the logarithms of the independent variables. Since the left-hand side of equation 2 can be closely approximated by the linear expression 3.2 R – 2 for 0.2 < R < 0.9, as long as recovery is restricted to that range, there is no practical difference between the empirical and the phenomenological equations.
A well-conceived phenomenological equation should behave properly for limiting values of the independent parameters. Although equation 1 gives correct results for limiting values of H, L, and V, it incorrectly predicts R → 1 as F → 0. To correct this defect, equation 1 was modified to
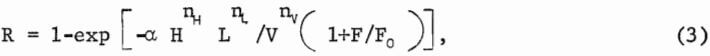
with the single adjustable parameter Fo replacing nF. Nonlinear regression was required to determine the adjustable parameters. A standard computer program gave the following values:
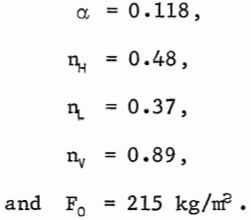
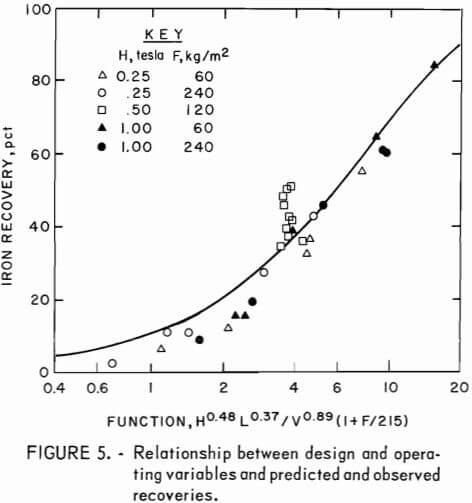A plot of experimental and calculated values of R versus the appropriate function of the independent variables is shown in figure 5. As can be seen from the range of the midpoint values of recovery, equation 3 adequately represents the data within the limits of experimental error. Although the fit could be improved by a more sophisticated model, the precision of the data probably does not warrant the introduction of the additional adjustable parameters that would be required.
The utility of a simple phenomenological equation as an aid in separator design can be illustrated by an example requiring only the simplest mathematical analysis. A feature of equation 3 that makes it particularly useful for design purposes is that matrix loading is defined per unit cross-sectional area rather than per unit volume. This formulation of the independent variables allows the effects of matrix length and matrix cross section to be evaluated independently and avoids the implication that the effect on metallurgical performance of loading per unit matrix volume is independent of matrix canister shape. For example, it is unlikely that, for a given mass of retained magnetics, canister A of 10-m² cross-sectional area (fig. 6) has retained over its 1-meter length the same distribution of magnetics that canister B of 1-m² cross-sectional area has retained over its 10-meter length. In terms of the design and operating parameters, the retention time of the slurry in the matrix is equal to L/V. For a given rate of slurry flow through the matrix canister, the retention time is determined by the canister volume. If recovery is controlled by retention time, the shape of Device B (fig. 6) would be operated at 10 times the flow velocity of A to give the same capacity and recovery. For retention time to be a valid design concept, the exponents nl, and nv in equation 3 must be nearly equal. For the magnetic scavenging results that have been discussed, the exponent nv was more than twice nL.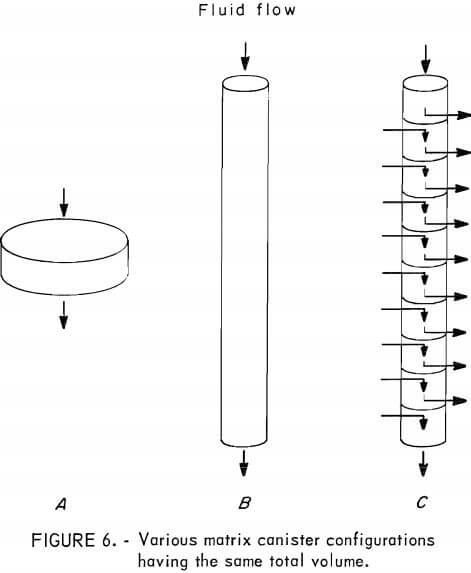 
Thus, for a given magnetized volume, configuration A, with a large cross-sectional area and small bed depth, gives optimal recovery. In fact, even if nL and nv were equal, configuration A would give better performance, because, for a given volume of feed slurry treated, matrix loading per unit area would be less. In principle, device B could be converted to give the same performance as A if the matrix were divided into 1-meter segments, as shown in C, and a suitable flow distribution system were provided.
Practical Aspects of Effective Separator Design
Models developed from bench-scale tests are valuable for designing pilot- or full-scale WHIM separators only when the larger machines offer the same degree of control over operating parameters that laboratory units do. One important feature lacking in many continuous units is control over flow velocity by means other than the natural resistance of the matrix bed. The Bureau of Mines’ pilot plant experience has indicated several other important features of effective separator design. The applied magnetic field should be reasonably uniform across the cross section of matrix through which the feed slurry and rinse water flow. Adequate provision should be made for rinsing the matrix with clean water in the high magnetic field region. The nonmagnetic , rinse, and magnetic products should be effectively separated. The design should avoid areas where particles can settle out and accumulate, such as flat-bottomed sections, regions of stagnant flow, and high-gradient regions outside of the matrix.
Probably the most important problem encountered with pilot- or full-scale WHIM separators is permanent retention of particles in the matrix. The effects may range from a slight decrease in recovery to complete clogging of the system. The first step in attempting to eliminate this problem is matching the matrix to the feed. The matrix elements should be spaced widely enough not to capture large particles by purely physical means. So as not to adversely affect magnetic capture of fine particles by excessive spacing of the matrix elements, it is advantageous to adapt the feed to the matrix by removing the oversized particles. Permanent retention of ferromagnetic particles in the matrix can be minimized by reducing magnetic flux leakage into the matrix flush zone and by choosing a matrix material of low coercivity and remanence. If a large proportion of ferromagnetics is present in the feed, it is desirable to use a conventional low-intensity magnetic separator before high-intensity separation. A critical factor for maintaining a clean matrix is a flush water velocity much higher than that of the feed slurry. For a given quantity of flush water, pulsating flow is preferable to steady flow; back-flushing is preferable to forward flushing. One of the most effective methods of assuring a clean matrix bed is to provide a method of agitating and rearranging the matrix elements.
Beneficiation of Oxidized Taconites
WHIM separation, either alone or in combination with flotation, is a technically feasible method of processing the enormous resources of oxidized taconite in the Lake Superior region. Commercial feasibility depends upon continuing progress in the design and construction of effective, reliable, yet economical magnetic separators. Mathematical models of separator operation can be valuable aids to the development of optimal designs. However, over dependence on unconfirmed theoretical descriptions, extrapolation of purely empirical results, and neglect of certain practical aspects of separator design can all lead to costly errors. Rational design of a full-scale separator for a particular application requires a realistic phenomenological model, supplemented by a systematic program of laboratory and pilot plant experimentation.
To help assure an adequate supply of minerals to meet the Nation’s economic and strategic needs, the Bureau of Mines is conducting bench- and pilot-scale research using wet high-intensity magnetic (WHIM) separation to recover iron from oxidized taconites of the Lake Superior region. The advantages and disadvantages of WHIM separation in relation to other separation methods, the most recent innovations in WHIM flowsheet design, and the role of mathematical models in process optimization are discussed.