The precipitation by zinc shavings is carried out in rectangular boxes or troughs, divided by transverse partitions into a number of compartments. The partitions are so arranged that the solution flows alternately downward through a narrow compartment, and upward through a wide one, the latter alone containing the zinc shavings. The height of every alternate partition is one or two inches lower than that of the succeeding one, so that the liquid, after ascending through a wide compartment, overflows the lower partition into the narrow space between it and the next (higher) partition; the lower edge of the latter is raised several inches above the floor of the box, so that the solution flows under it into the next wide compartment, and so on. (See Fig. 37.)

The dimensions of the boxes vary, according to the work required of them; the following may be taken as representing ordinary conditions: Length, 12 to 24 ft.; width, 1½ to 3 ft.; height, 2½ to 3 ft.

The sides, ends, and bottoms are usually constructed of 1½-in. boards, strongly held together by bolts passing horizontally from side to side of the box, generally through the narrow compartments. Vertical bolts are also used for securing the floor of the box to the sides. The partitions, which may be of thinner boards, fit into vertical grooves.

The box is preferably raised somewhat above the floor of the extractor house, and should have a slight fall from the feed to the discharge end. Sometimes the bottom is inclined to one side, and plugs are provided on this side just above the bottom, so that the precipitate may be easily collected during the clean-up. The advantage of this latter arrangement is somewhat doubtful, as it may lead to losses through leakage, etc.

In each of the wide compartments is a tray, resting loosely

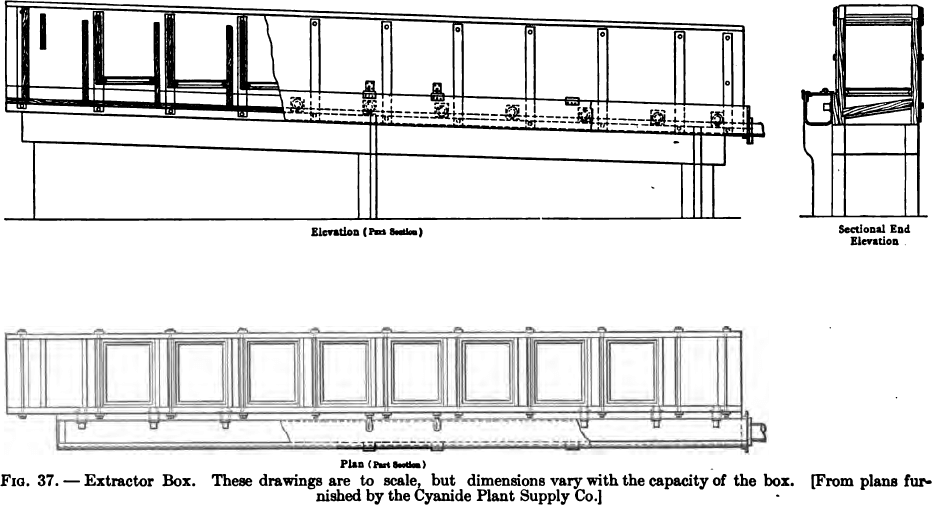
on supports fastened to the sides of the box. The bottom of this tray is formed of wire screening, generally with, four holes to the linear inch, and serves to hold the zinc shavings. The sides are of wood, with iron handles by which the tray may be lifted out of the box when necessary. The last compartment, at the exit end of the box, has an outlet near the top, from which a pipe leads either to the storage tanks or to a small sump whence the precipitated solution is pumped to the storage tanks.

Zinc-boxes of similar design are also constructed of iron or steel, painted or enameled so as to resist the action of cyanide or alkali solutions. For further details of zinc-box construction, see Julian and Smart.

CIRCULAR VATS FOR ZINC PRECIPITATION

W. A. Caldecott has advocated the use of circular vats in place of zinc-boxes for precipitation. The vat is filled with zinc shavings resting on a circular perforated tray. The solution is introduced from below and ascends evenly through the mass of shavings. The exit pipe is placed near the top of the vat, and extends to the center, being bent upward at the orifice. The advantages claimed are that the tendency to uneven flow observed in rectangular boxes is avoided, that there is less liability to leakage, and that there is economy of space as compared with ordinary boxes. In the rectangular box there is a likelihood of channels of easy flow occurring at the sides and especially at the corners of the compartments, leading to imperfect precipitation, unless great care is exercised in packing the shavings into the box.

A further development of this idea is due to P. S. Tavener, who uses a circular vat with a conical bottom. A stirrer mounted on a central vertical axis has paddles which revolve in the space beneath the perforated bottom. At the clean-up, the precipitate which passes through the screen may thus be swept toward the central discharge hole. The solution to be precipitated descends through a central column and ascends through the perforated bottom, passes through the mass of zinc shavings, and overflows into a circular launder at the top of the vat.

CUTTING AND PREPARING THE ZINC SHAVINGS

The shavings are prepared from sheet zinc, which is cut into disks punched in the middle, so that a large number can be set side by side on a lathe. While rapidly revolving, a chisel is held against the edges of the disks. The width and thickness of the shavings can be varied within certain limits by the manner of holding the cutting tool, and by altering the speed of revolution.

There is considerable difference of opinion as to the best thickness for the zinc shavings. As effective precipitation depends on exposing a large surface to the liquid, it would seem that the shavings should be cut as fine as possible; on the other hand very fine shavings rapidly dissolve or break to pieces, and eventually form lumps which choke the zinc-boxes, giving a precipitate full of small pieces of zinc which is very troublesome to smelt. Ordinary commercial zinc is preferable for this purpose to chemically pure zinc, owing to the electrical actions set up by the contained impurities, but very impure zinc should not be used, especially if containing much arsenic and antimony, as these metals may give rise to much trouble in the subsequent treatment of the precipitate. For effective work, the shavings should be freshly prepared, and as free as possible from oxide.

LEAD-ZINC COUPLE

In order to increase the efficiency of the zinc for precipitating, it is a very usual practice to dip the shavings, before charging them into boxes, in a 1 to 5 per cent, solution of lead acetate, which causes an immediate deposit of finely-divided lead on the surface of the zinc. This forms a powerful galvanic couple, which is capable of depositing gold from solutions much weaker in free cyanide than can be precipitated by the ordinary zinc shavings. In cases where much copper is present in the solution, the use of zinc-lead couple is often advantageous. The upper compartments, in this case, are filled with ordinary shavings and serve to precipitate gold and silver; in the lower compartments are placed the shavings which have been dipped in lead acetate these precipitate copper much more energetically than the plain zinc shavings, and so prevent this metal from accumulating in the solution to an injurious extent. This important improvement in the zinc precipitation process was introduced by J. S. MacArthur at the Lisbon Berlyn mine, Lydenburg, Transvaal, about 1894, with successful results, but does not appear to have been adopted elsewhere until it was brought forward at Johannesburg, in 1898, by W. K. Betty and T. L. Carter.

CHARGING THE ZINC INTO THE BOXES

The best results are obtained when the zinc forms a homogeneous, spongy mass. The compartments should be well filled, but the shavings should not be pressed down too tightly. Especial care should be taken in filling the corners, and any parts where it appears likely that channels may form. The boxes should be inspected from time to time while the solution is passing through and any irregularities in the flow rectified by adding fresh shavings, if necessary. A plan sometimes adopted is to arrange the shavings in layers crossing each other alternately at right angles. The zinc is cut into very long threads, as thin as possible without becoming too brittle; these are laid in separate bundles on the trays in each compartment; another layer of bundles is placed over these at right angles. This arrangement is said to be very effective in preventing irregular flow.

The quantity of zinc to be used per cubic foot of space varies considerably, according to the manner in which it has been cut and other circumstances. The action of the solution on the zinc is naturally most active near the head of the box; as the zinc dissolves in the top compartments, the shavings from the lower compartments are taken out to replace them, and fresh zinc is placed in the lower compartments.

The first and last compartments of the box are frequently left empty, the first as a safeguard against suspended matter which might be carried through by the solution and deposited on the zinc, and the last as a trap to retain any fine precipitate which might be carried over by the flow of solution, especially during the transfer of shavings from one compartment to another or during any disturbance of the box. The last compartment has occasionally been filled with coke or sawdust, with the object of filtering out any finely divided precipitate which might be contained in the effluent. This compartment would, in the latter case, only be cleaned up occasionally, perhaps once in three months, when the filtering material would be burned and the values recovered by smelting the ashes. Whenever the zinc in the boxes is to be moved or disturbed in any way, the flow of solution should be cut off or diverted to another box, to avoid the danger of suspended gold precipitate being carried out of the boxes in the effluent solution.

The boxes should be “ dressed ” at least twice a day, and fresh zinc added as required. Careful attention to the filling of the zinc-boxes is a very important factor in the successful operation of the process.

CONDITIONS WHICH INFLUENCE PRECIPITATION

The principal conditions on which satisfactory precipitation depends are: (1) the freedom of the entering solution from solid matter in suspension; (2) the presence of a sufficient amount of free cyanide; (3) the presence of sufficient free alkali; (4) the absence of excessive amounts of foreign salts, particularly of copper and iron compounds; (5) a regular and uniform flow of liquid through the box; (6) a sufficient volume of zinc per ton of solution to be precipitated per day; (7) a clean, unoxidized surface, on which the gold and silver are deposited in a loose flocculent condition, easily detached.

Influence of Suspended Matter

The precautions usually taken to prevent the entrance of suspended matter — sand, slime, organic substances, etc. — into the boxes have already been described (Part IV, Section IV, B). When such substances are present they are not only liable to coat the zinc shavings with deposits of different kinds, thus interfering mechanically with the precipitation of the precious metals, but the foreign matter thus introduced adds greatly to the expense and trouble of the smelting operation, extra fluxes being required to remove it. Where efficient settling tanks or clarifiers are not provided, it is customary to leave the first wide compartment of the box empty with the object of collecting any sediment. In some cases this compartment is filled with coarse sand, coir fiber, or other filtering medium.

Influence of Free Cyanide

When ordinary zinc shavings or filaments are used for precipitation, it is found that the precipitation of gold and silver is very much more effective in solutions carrying a fair amount of free cyanide than in solutions weak in cyanide. The strength of the entering solution should never be allowed to fall much below 0.2 per cent. KCN, and in some cases it is advantageous to allow a strong solution to drip slowly into the top compartment of the box, to ensure a sufficient strength for good precipitation. When the zinc-lead couple is used the matter is of less consequence and very weak solutions can in general be precipitated by it. T. L. Carter found that solutions of 0.005 to 0.008 per cent, free cyanide could be satisfactorily precipitated, with an extraction of 90 to 95 per cent, of the gold, using the zinc-lead couple and a drip of strong cyanide at the head of the box, so that at the beginning the strength of the entering solution was raised to 0.025 per cent.; after 12 or 14 hours the strength was allowed to fall to 0.008 per cent. Other workers using the lead-zinc couple have found the strong cyanide drip quite unnecessary. Occasionally a drip of lead acetate solution is used.

It would appear that the presence of some other salts besides cyanide may in certain cases induce good precipitation of gold on zinc, for it has been observed that solutions which have become very “foul,” that is, highly charged, with accumulated salts, chiefly complex cyanogen compounds of iron, zinc, copper, etc., sometimes precipitate their gold contents on clean zinc better than solutions otherwise pure, but weak in free cyanide, and it is even possible to precipitate in the complete absence of free cyanide. Another advantage of a sufficient strength in free cyanide is that the formation of injurious deposits in the boxes is largely prevented. The so-called “white precipitate” consisting of hydrate, cyanide, and ferrocyanide of zinc, chiefly occurs in boxes where weak solutions are precipitated. Strong cyanide solutions also are less liable to precipitate copper in preference to gold.

Influence of Alkali

A certain minimum of free alkali is found to be essential for good precipitation. On the other hand, a large excess should be avoided. Whether alkalies actually decompose the double cyanides of zinc with liberation of free cyanide appears somewhat doubtful, but their presence undoubtedly increases the solvent efficiency of these compounds, and also promotes precipitation. They are also solvents for some at least of the constituents in the white precipitate referred to above.

Excessive amounts of alkali cause a violent action on the zinc, with great waste of the metal, accompanied by “ foaming,” due to the evolution of large quantities of hydrogen, and a tendency for the gold precipitate to be detached and carried away by the flow of solution. Too large a quantity of lime in solution may lead to the deposition of insoluble calcium compounds, carbonate or sulphate, on the surface of the zinc, owing to reactions between the lime and the soluble carbonates and sulphates present as impurities in the cyanide or extracted from the ore. During the passage of solution through the boxes an increase of alkalinity is invariably observed. This is explained in the section dealing with the chemistry of the process.

It is occasionally found necessary to add alkali, either in the zinc-boxes themselves or in the storage tanks. In some cases addition of sodium carbonate to the solution in the sumps has a beneficial effect, as it precipitates salts which might otherwise cause a deposit of insoluble carbonates in the boxes.

Rate of Flow

Under a given set of conditions the slower the rate of flow the more complete will be the precipitation. It is found, however, that an increased rate of flow may be compensated for by increasing the surface of zinc with which the solution must come in contact; and as a rapid flow has other advantages, it is generally good practice to pass the solution through the boxes as rapidly as is consistent with efficient precipitation.

In the early days of the process it was considered necessary to use about ¾ cu. ft. of zinc shavings to precipitate the solutions used in treating each ton of ore per day; according to modern practice, as much as 7 or even 12 tons of solution can be precipitated per cubic foot of zinc per day. The actual rate of flow in the latter case may be from 7 to 13 cu. ft. per minute across a section of 14 sq. ft. of zinc, or 0.5 to 0.92 ft. per minute for each square foot of section. This method, however, can only give good results when much care is taken in charging the compartments.

According to Caldecott and Johnson, a pound of ordinary zinc shavings exposes about 40 sq. ft. of surface; a cubic foot of the shavings, as usually packed in the compartments, would weigh from 3.5 to 4 lb., and hence exposes a precipitating surface of 140 to 160 sq. ft. Taking the volume of a ton of solution as 32 cu. ft. (Part IV, Section IV), a zinc-box of 8 compartments, each containing. 4 cu. ft. actually occupied by zinc shavings, would contain at any moment 1 ton of solution undergoing precipitation and exposed to a precipitating surface of about 4800 sq. ft. If 1 ton of solution be precipitated per cu. ft. per day, 32 tons of solution must pass through the box per day; in other words, the rate of flow will be 1 ton in 45 minutes.

Nature of the Precipitating Surface

It has already been pointed out that the best results are usually attained by cutting the zinc in very long, thin threads. These usually have a thickness of 1/250 to 1/1000 in. and a width of 1/16 to ¼ in., but practice varies very widely in these particulars. The smaller surface exposed by thick shavings may be largely compensated for by using the lead-zinc couple and thus obtaining greater precipitating efficiency. Mixtures of lead and zinc shavings, and shavings prepared from an alloy of zinc containing 3 per cent, of lead, have also been used, and are more effective, especially with solutions weak in cyanide, than ordinary zinc shavings. These combinations, however, are less generally adopted and probably less energetic than the couple formed by immersing the zinc in a solution of a lead salt.

Zinc-copper and zinc-mercury couples have also been tried, and are as efficient as the zinc-lead couple in promoting precipitation of gold and silver; but they have certain serious drawbacks. Mercury causes the shavings to fall to pieces and rapidly reduces them to a pulpy mass, from which the mercury may be separated by squeezing through a cloth. When copper is used for this purpose, a very base bullion is obtained in the smelting of the precipitate.

Great care must be taken to expose the shavings to the atmosphere as little as possible. When charged into the boxes, they should be freshly turned, clean and unoxidized; the compartments should be filled so that about an inch of solution is left over the top of the zinc, and the moist shavings especially should never be exposed to the air any longer than absolutely necessary during transfer from one compartment to another.

It may generally be assumed that satisfactory precipitation is taking place when the deposit of gold and silver is in a loose condition and of a brownish-black color. When a smooth, coherent, metallic deposit is observed, the precipitation soon ceases altogether, and it is probable that some alteration is necessary in the conditions.

A vigorous, but not too violent, evolution of hydrogen also accompanies good precipitation; the reduction of the gold-alkali cyanide and consequent precipitation of the gold is commonly supposed to be due to nascent hydrogen, that is, to an action taking place between the gold compound and the hydrogen at the moment when the latter is set free by the decomposition of water, as explained in Part II. On the other hand, the accumulation of bubbles of hydrogen on the surface of the zinc hinders precipitation. The gas in this form has no action whatever on the gold compound, and prevents contact between the solution and the zinc surface. Hence the occasional removal of the bubbles by shaking or turning over the zinc shavings tends to promote good precipitation.

DIFFICULTIES IN ZINC PRECIPITATION

These difficulties have already been alluded to in discussing the conditions which influence precipitation; it may, however, be of advantage to recapitulate them. They are: (1) Deposition of suspended matter on the surface of the shavings. (2) Formation of insoluble compounds coating the shavings, by chemical action of cyanide, alkali, or other substances on the zinc. (3) Formation of insoluble compounds by subsidiary actions going on between various substances in the solution passing through the boxes. (4) Formation of thin metallic coatings (of gold, silver, copper, etc.), which protect the zinc from the solution and so check further precipitation. (5) “ Polarization ” of the zinc, by accumulation of hydrogen bubbles on its surface. (6) Imperfect deposition of gold and silver from solutions not sufficiently strong in cyanide. (7) Excessive consumption of zinc under certain conditions. (8) Irregularities of flow due to the formation of channels, thus leading to inefficient precipitation.

Deposits Formed by Action of Solution on Zinc

These are generally due to insufficiency of free cyanide. Researches on the nature of these deposits have shown that they generally consist principally of hydrated zinc oxide, presumably formed by the oxygen liberated in the electrolysis of water by the various metallic couples present in the box, in which the zinc acts as anode. Relatively small quantities of zinc cyanide may also be present. As these compounds are soluble in a sufficiently strong cyanide solution, the obvious remedy is to increase the strength of the solution entering the box by addition of cyanide, but this is not always practicable. When large quantities of iron are dissolved from the ore as ferrocyanides, there may be a precipitation in the boxes of ferrocyanide of zinc, or of some insoluble double ferrocyanide of zinc and an alkali metal. These deposits are still more troublesome as they do not readily redissolve, either in cyanide or alkali. In many cases the only remedy is, after the deposit has accumulated to a certain extent, to clean up the box and start afresh with clean zinc. Ammonium salts and sodium chloride have sometimes been added as solvents for deposits of insoluble zinc compounds.

Caldecott and Johnson (loc. cit.) appear to consider that a mixture of lead and zinc shavings is preferable to the lead-zinc couple in cases where deposition of zinc hydrate takes place; they state that “ a mixture of lead and zinc shavings has a lengthy efficiency, possibly due to the fact that the zinc hydrate does not coat the whole couple to the same extent as with the usual lead- coated zinc shavings.”

Other Deposits Due to Subsidiary Reactions

The deposition of calcium carbonate and sulphate in the boxes has already been mentioned. Under certain conditions alumina, and possibly silica from soluble silicates, may separate out. Solutions containing manganese very readily throw down a brown hydrated oxide of the metal.

Sulphur, either as finely divided pyrites carried through mechanically and settling on the shavings, or as sulphide of zinc due to the reaction between zinc hydrate and alkaline thiocyanates in the solution, is also frequently present, and when iron or other base metal is contained in the precipitate may give rise to the formation of a matte during the smelting.

At Redjang Lebong, Sumatra, selenium is precipitated in the zinc-boxes in considerable quantity, but no evidence is at hand as to the form in which it occurs. It is particularly troublesome, as it is extremely difficult to eliminate it completely in the subsequent operations, and its presence in the bullion even in small quantities is very detrimental, as it renders it brittle.

Arsenic, antimony, lead, and mercury, if present in solution, will also be deposited on the zinc. Tellurium probably acts similarly to sulphur and selenium.

“ Metallic ” Coatings

As already pointed out, gold is sometimes deposited, not in a loose flocculent condition, but as a bright metallic coating having the natural color of gold. This occurs chiefly when the solutions are either very rich in gold, or low in cyanide. There are considerable grounds, as pointed out by Argall, for supposing that the ordinary loose precipitate is a compound of zinc, gold, and cyanogen, while the metallic coating referred to above is probably gold in the elementary state. Similar metallic coatings may be formed with silver, copper, and mercury, and when they occur, further precipitation in those parts of the box in which they are formed is almost entirely arrested. It has been found that the activity of the coated shavings can be restored by immersing them for a few moments in dilute sulphuric acid, washing in water, and at once replacing in the boxes.

Consumption of Zinc

The normal consumption of zinc on a cyanide plant is from 0.25 to 0.5 lb. per ton of ore treated, but in special cases it may be considerably more or less than these amounts. Only a portion of this is actually dissolved by the solution, and of that which is dissolved, only a small part corresponds with the gold or silver precipitated. A large part goes in the form of small fragments of metallic zinc into the precipitate collected during the clean-up, and a further quantity is dissolved by subsidiary reactions with cyanide, alkali, or oxygen from decomposition of water, as already described. We may thus distinguish two sources of consumption, mechanical and chemical, the former including all zinc passing in a solid form into the precipitate, and the latter all that goes into solution. When strong cyanide solutions are used the chemical loss is greater, but the mechanical loss is less than with weak cyanide solution.

The following particulars, given by W. H. Virgoe with regard to two Mexican plants, treating sand and slime respectively, are of interest in this connection.

The curious feature of these results is that the total consumption of zinc per ton of ore treated was practically the same in both plants, but the nature of the loss was entirely different, being chiefly chemical in the case of the sand plant, where strong solution was used, and chiefly mechanical in the slime plant, where the solution entering was very weak in cyanide. In the latter case the gold was no doubt largely deposited as a thin film which could not be detached from the shavings by slight rubbing, so that a large quantity of metallic zinc had to be smelted in order to recover the values.

Estimating the consumption of zinc merely by the amount used up per ton of ore treated may give a false idea of the work actually done by the boxes; a more exact gauge of efficiency is often obtained by considering the amount of zinc consumed per ton of solution passed through, or per ounce of gold or silver precipitated. On the latter basis, the efficiency of zinc for precipitating silver is generally much greater than for gold, chiefly because the entering solutions carry a much larger percentage by weight of precious metal. Heavy mechanical losses of zinc are generally due to errors either in the preparation of the shavings, or in the handling of them during the passage of solution or during the clean-up. Badly cut shavings are apt to give large quantities of small fragments, which pass into the precipitate, and many causes, such as uneven flow resulting in channels, exposure to atmosphere, and unnecessary handling, tend to make the zinc brittle. The deposition of gold, etc., in a thin coherent film is also, as pointed out above, a cause of mechanical loss.

The causes of chemical loss have already been fully discussed. It has been considered that losses may occur through contact of zinc with iron surfaces, as for example in the screens used to support the shavings in the compartments. This, however, is practically unavoidable, and it does not appear probable that the loss from this cause is serious, since the iron rapidly becomes coated with a film of oxide or carbonate that acts as an insulator.

Precautions against Theft.— It is customary to cover the tops of the zinc-boxes with wire screening, or with locked lids, which are only opened when it is necessary to transfer shavings or during the clean-up and refilling of the boxes. In many plants the precipitation and smelting departments are strictly isolated from the rest of the establishment, and only those directly concerned are admitted.

NON-ACCUMULATION OF ZINC IN THE SOLUTIONS

It is a remarkable fact that although zinc is constantly dissolving during the passage of the solution through the boxes, the average amount of it in the solution remains about stationary after it has once reached a certain point. It is evident, therefore, that somehow zinc is being removed from the solution. The amount of solution thrown away in the residues and replaced by fresh water does not afford a sufficient explanation. Some portion is no doubt redeposited in the boxes as insoluble zinc hydrate, etc., from solutions weak in cyanide; some may be precipitated in the ore or in the boxes as zinc sulphide, by soluble sulphides. Soluble sulphides of the alkali metals may be present in commercial cyanide, formed by the action of alkali on sulphides in the ore, or formed by reduction in the zinc-boxes through the action of nascent hydrogen on the thiocyanates, which are almost invariably present in the solutions when the ore under treatment contains pyrites. W. H. Virgoe has suggested that in presence of lime and carbonic acid there may be a precipitation of double carbonate of zinc and calcium, as follows:

K2Zn(CN)4 + 2Ca(OH)2 + 2CO2 = ZnCa(CO3)2 + Ca(CN)2 + 2KCN + 2H2O.

TESTS FOR REGULATING THE WORKING OF THE BOXES

The methods used in making these tests will be fully described in a later section of this book. Samples of the solutions entering and leaving the boxes should be taken at frequent intervals. This is generally done by means of glass tubes provided with cocks and passing through the top and bottom ends of the boxes. The cock is turned so as to allow a small uniform drip of solution, which is caught in a bottle beneath. These samples are tested at regular intervals, say every 12 or 24 hours, for cyanide, alkali, and gold (for silver also where this metal is of importance). These represent the average results for equal periods of time. Special samples for cyanide and alkali are generally required at more frequent intervals for regulating the leaching operations, the supply of cyanide for the storage tanks, etc., and a test is commonly made of each solution run on and drawn off from each charge under treatment, unless the material is so uniform and the conditions so regular as to render this unnecessary.

The strength of cyanide to be maintained depends on such a variety of circumstances that no general rule can be given. Some information on this head will be found in Part IV, Section I.

The alkalinity needed also depends to a certain extent on the nature of the material under treatment. A slight but constant alkalinity should be maintained in the entering solution, this being secured by the addition of suitable amounts of lime to the ore or pulp to be treated, or, occasionally, by the addition of caustic soda to the solutions themselves. For slimes plant solutions, W. A. Caldecott recommends an alkali strength equivalent to 0.006 to 0.01 per cent. NaOH, but frequently as much as 0.05 per cent, or more is admissible.

Clean-Up of Zinc-Boxes

PRELIMINARY OPERATIONS

The frequency of the clean-up will depend on the nature and amount of the precipitate which is formed. In large plants it may take place once a week, in small ones once a month, the common practice being twice or three times a month. When much white precipitate has formed, it may be necessary to clean up oftener than would be the case with a clean gold deposit containing the same values. Before cleaning up it is usual to displace the solution in the box with water, to which alum may be added to promote settlement of the precipitate during the process. In some cases the strength of the entering solution is raised considerably for an hour or so before it is displaced with water. This is for the purpose of loosening the deposit which adheres to the zinc. After all cyanide has been displaced, a little acid may be added, which also assists settlement.

SEPARATION OF PRECIPITATE FROM COARSE ZINC

The trays are first lifted in the compartments, and shaken up and down to allow as much of the precipitate as possible to pass through the screen. The operator, wearing rubber gloves, generally also shakes the shavings under water in the compartment, and then holds them over an adjoining (lower) compartment where they are sprayed with a jet of water. In some cases the tray and contents are lifted bodily from the box and placed over the clean-up tank, into which the fine adhering precipitate is washed. The washed shavings are then either set aside in any suitable water-tight vessels, such as enameled-iron pans, buckets or trays, or are transferred to the lower compartments of another zinc-box. Each compartment in succession is treated in this manner, beginning at the head and proceeding to the foot of the box.

REMOVAL OF PRECIPITATE FROM BOX

After the whole of the coarse zinc has been lifted out, the trays are turned over, washed and scrubbed to detach any adhering precipitate.

The liquid and precipitate remaining in the box are then transferred to a special settling tank, usually about 4 ft. diameter by 3 ft. deep, known as the clean-up tank. This is generally of wood, sometimes lined with lead. As this tank is often used, for the subsequent acid treatment of the precipitate, it is sometimes provided with a wooden paddle mounted on a central vertical shaft, or with other means of stirring. When there are no outlets to the compartments, the transfer is made by means of enameled-iron buckets. In some plants, the contents of the box are allowed to stand and settle for some time, and the clear liquid syphoned off. The residue is then scooped out and carried to the clean-up tank. When plugs are provided at the bottom of the compartments, these are pulled out and the liquid allowed to run into a launder beneath, which leads to the clean-up tank. The sides of the compartments are then washed down with a hose until the whole of the precipitate has been cleaned out and run into the tank. When the box is perfectly clean, the coarse zinc is replaced on the trays in the same order, unless it has been already transferred to another box. The box is at once filled up with solution, so as to avoid oxidation of the zinc, and is ready for use after any fresh zinc that may be necessary has been added.

In some modern plants, the whole of the liquid drawn off during the clean-up is passed through a small filter-press. The precipitate, after passing through a fine screen (60- to 80-mesh), is also filter-pressed, and the material retained on the screen treated separately. Formerly the fine precipitate was squeezed by hand through filter-bags.

SETTLEMENT AND SIFTING OF PRECIPITATE

Where filter-presses are not used, the liquid is allowed to stand for 24 to 48 hours in the clean-up tank, sometimes with addition of a little alum, until the precipitate has completely settled. The clear liquid is then carefully syphoned off and run to waste. The precipitate during transfer to the settling tank is frequently run through a fine sieve, 40- to 80-mesh, and any material retained on the sieve (generally known as “shorts” or “ metallics ”) is set aside for separate treatment. When sufficiently coarse, it may be returned to the top compartment of the box and placed on a layer of clean shavings; if there is too much of this product, however, or if it is too fine, it would be liable to choke the screens of the boxes, and it is usually treated with acid to dissolve as much as possible of the zinc, as described below.

If acid treatment is not to be used, the settled precipitate, if free from shorts, may be at once pumped to a filter-press. Lead-lined tanks should not be used when the precipitate, as is often the case, contains mercury, as this metal amalgamates with the lead and rapidly corrodes the lining.

In some plants vacuum filters are used. As the precipitate is very finely divided, the filtering medium must be very closely woven, such as flannel or very thick canvas. The liquid is drawn off by a suction pump and a wash of fresh water added, and this is again sucked through to extract as much as possible of any soluble matter which may be present. Any wash-waters drawn off in the above processes should be assayed before finally running to waste, as they occasionally carry sufficient values to be worth recovering. In that case they should be returned to the boxes, after addition of alkali, if necessary.