Table of Contents
Calculating material flows from analytical data by means of the standard two-product formulas grew increasingly difficult and time-consuming as the complexity of the flowsheets increased and as choices between conflicting analytical values had to be made.
Mathematical Formulation of the Problem
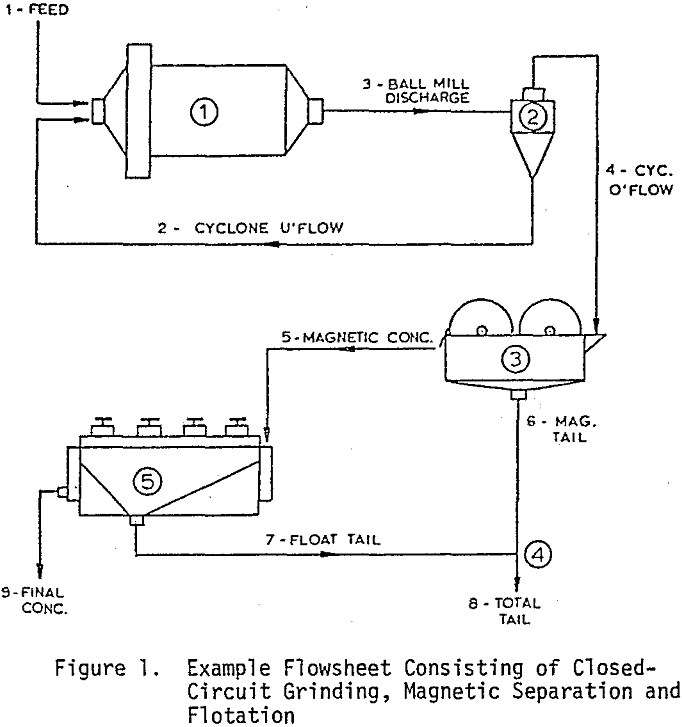
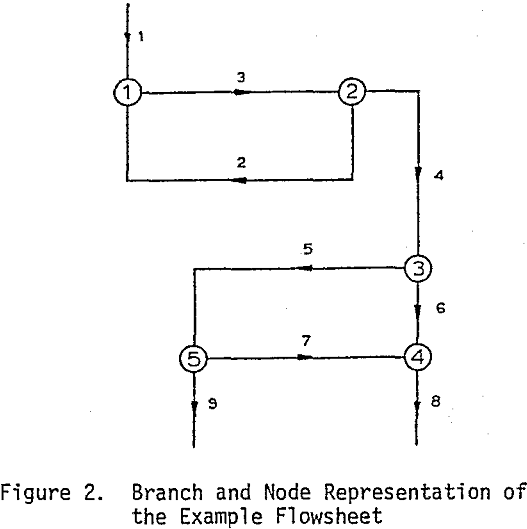
Any metallurgical flowsheet can be represented by a set of directed lines called branches. These branches represent steady state flows of the various process streams in the flowsheet, e.g., “feed”, “cyclone overflow”, etc.
Junction points where two or more branches come together are called nodes. Nodes usually represent an operation such as flotation or thickening or simply a point where process streams become combined or divided.
The flowsheet can be redrawn as a set of connected lines. The lines (branches) and the connecting points (nodes) are conveniently identified by numbering them. If the symbols B and N are used to represent the number of branches and number of nodes, then B = 9 and N = 5 in this example.
Any flowsheet can be unambiguously described by an N x B matrix called the F (for flowsheet) matrix whose elements are 0, -1 or +1. If the flow of the jth branch is into the ith node, element Fij is -1; if the flow of the jth branch is away from the ith node, Fij is 1. If the jth branch does not connect to the ith node, the value of Fij is 0.

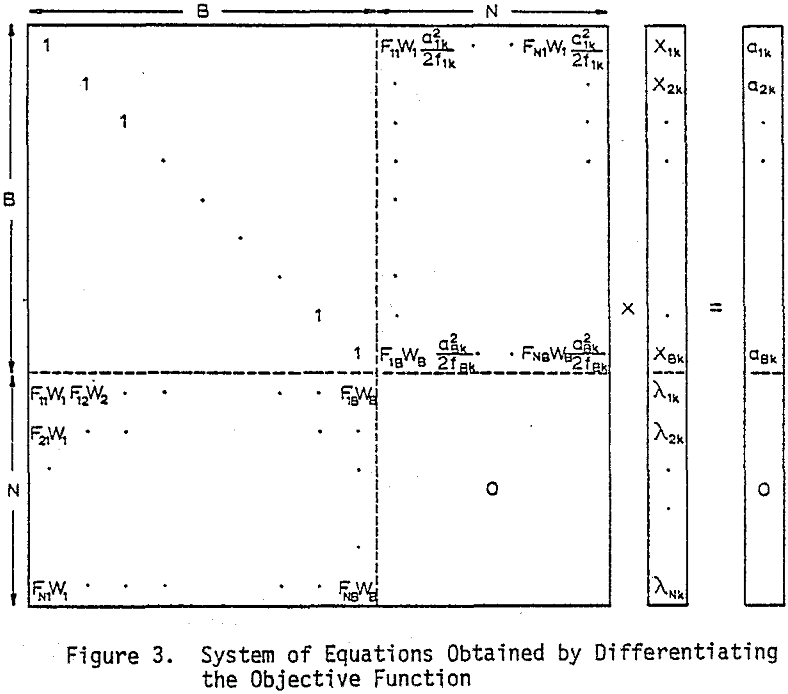
In addition to the F matrix, each metallurgical balance problem has certain given data such as experimental analyses, ajk, of the jth branch for the kth component and given weights, Wj, of the jth branch.
The experimental analyses, ajk, are estimates of the “true” analyses, Xjk, and are assumed to deviate randomly about X with a standard deviation proportional to a. The assumption of relative deviations is consistent with the analytical practice of performing analyses to a certain relative accuracy rather than to constant level of accuracy.
Solution of the Mathematical Form
A far simpler method, and the one used in the computer program described here, is to treat the second and fourth terms of the objective function separately from the other terms to obtain a solution for the W’s as a function of a subset of independent W’s. Substituting these W’s into the remaining terms of the objective function and taking derivatives then provides linear equations with which to solve for the X’s and thereby evaluate the objective function. By systematically varying the subset of W’s with an efficient search routine, the minimum of the objective function can be readily obtained, with the values of the X’s and W’s at that point being the solution to the problem.

Program Description
Input to the program consists of the flowsheet parameters (number of nodes, number of branches, etc.), the component and branch names, and the given analyses and weights. All data are read in free format. The program scans the component names to determine if a component is a screen analysis or percent solids so that appropriate action can be taken.
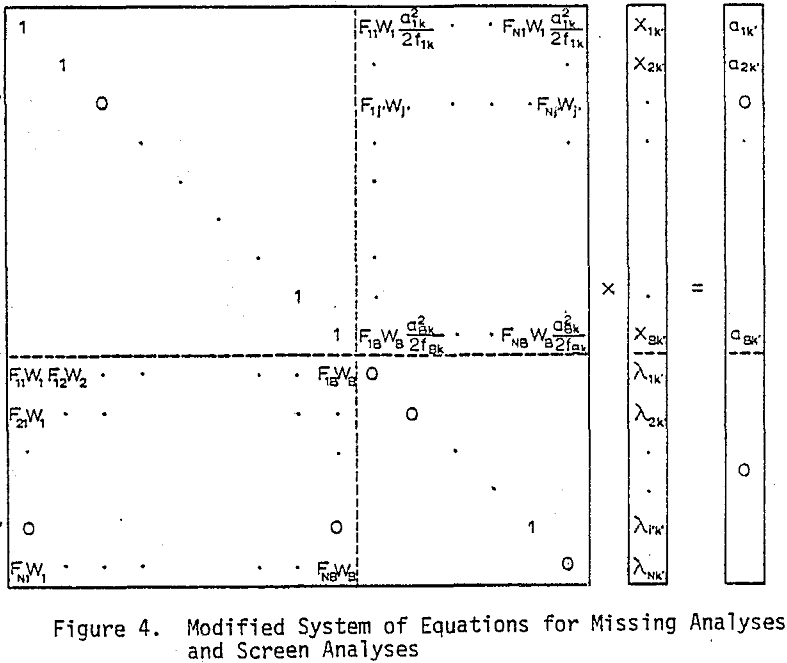
Two lines of input are used for each branch. The first line consists of a branch name of up to 22 characters. The second line consists of the numbers of the nodes to which the branch is connected, the values of the component analyses ajk, and the fixed weights, if any. A missing analysis is entered as a zero. If a negative analysis is entered, the analysis is not used in the calculations but its absolute value is printed in the final table. This is a convenient way of inserting supplementary data into the output.
There are three options for setting the values of the weighting factors fjk. The first option sets all the factors to one; the second reads in separate factors for each component, the third reads in individual factors for each analysis.
The values of the dependent and independent weights, the analytical values ajk and the F matrix are used to construct the H matrix of coefficients and the right hand side of the system of equations. If analyses are missing or if screen analyses or percent solids are involved, the system of equations is modified. The system of equations is then reduced to full rank if necessary and solved by a Gaussion elimination technique for the values of Xk.