Cutoff grade is defined as the grade that is normally used to discriminate between ore and waste within a given orebody. Although the definition of cutoff grade is very precise, the choice of a cutoff grade policy to be used during an exploitation of a deposit is not. Use of simply calculated breakeven cutoff grades during the production will in most instances lead to sub-optimum exploitation of the resource.

Traditional Cutoff Grades in Open Pit Mining

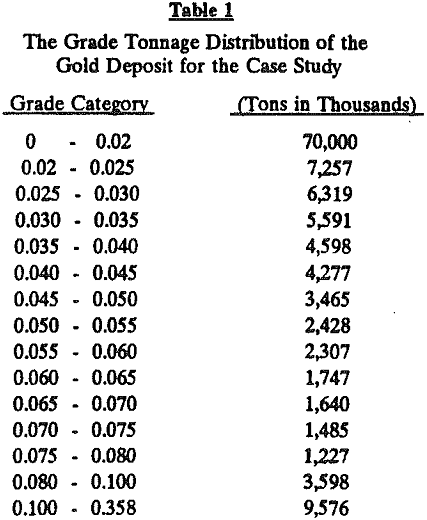
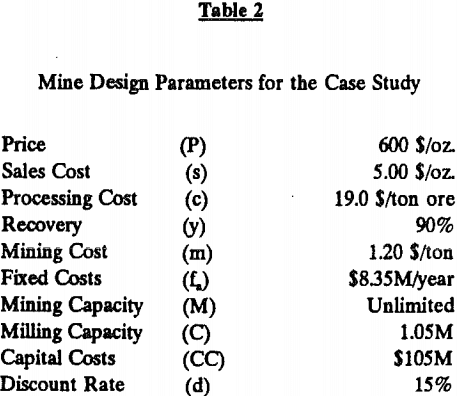
Consider a hypothetical case study where an epithermal gold deposit will be mined by an open pit Table 1 gives the grade distribution of the material within the ultimate pit limits of this deposit. Table 2 gives assumed capacities and accepted costs to mine this deposit at 3000 tons/day milling rate.

 

 

 

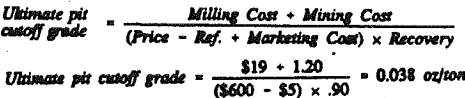
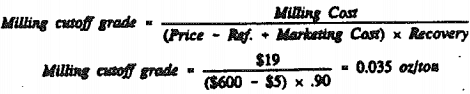
The second cutoff grade is used to ensure that any material that provides positive contribution beyond the direct milling, refining and marketing costs will be milled.

Heuristic Cutoff Grade Optimization Techniques

In Table 3, Qm represents amount of total material mined (in millions of tons) in a given year; Qc represents the ore tonnage (in millions) processed by the mill; Qr represents the recovered ounces (in thousands) produced in a given year. The annual cash flows are given as profits in millions of dollars and they are determined by using the following equation (see also Table 2 for variable definition):

Profits($M) = (P – s) x Qr -Qc x c -Qm x m

As long as the operators mine and process the blocks of material with grades greater than equal to static cutoff grades without considering deposit characteristics, only the undiscounted profits will be maximized.

The concept of using cutoff grades higher than breakeven grades during the early years of an operation for a faster recovery of capital investments and using breakeven grades during the later stages of the mine has been practiced in the industry for heuristic NPV optimizations.

 

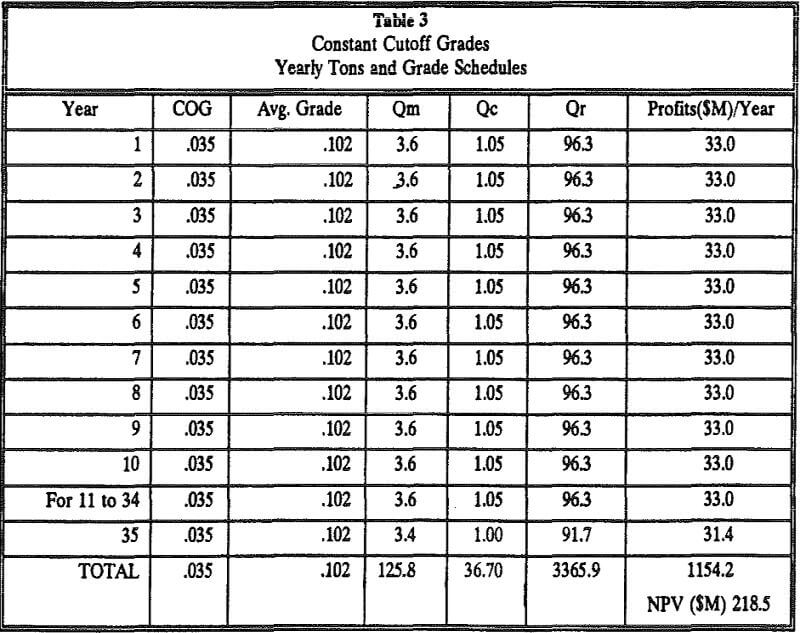
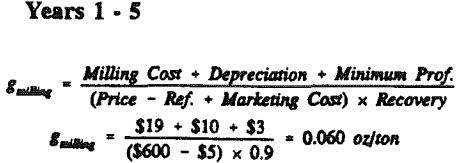
The year by year tons and grade schedule obtained from the modified cutoff grade policy is given in Table 4.

In the previous calculations the G & A costs were not included in the cutoff grade and profit calculations.

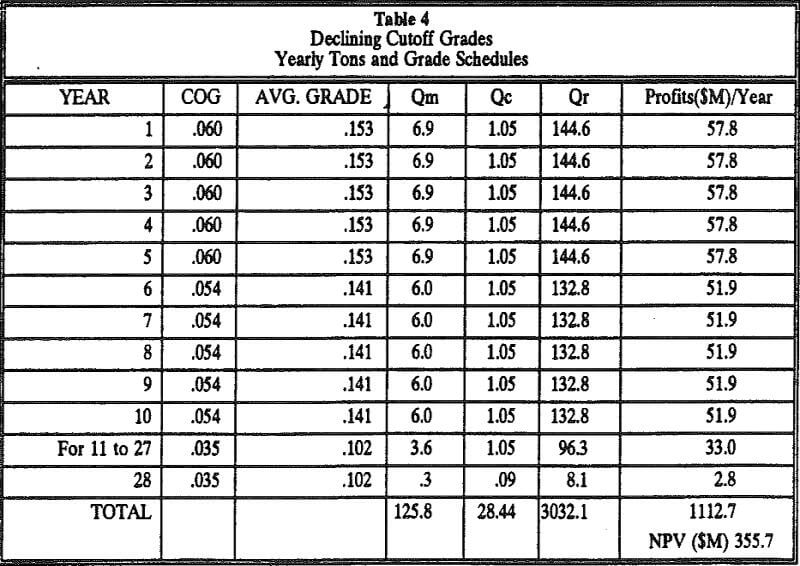
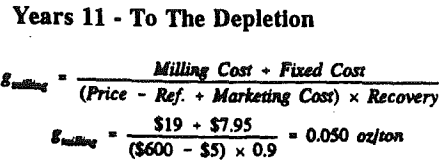
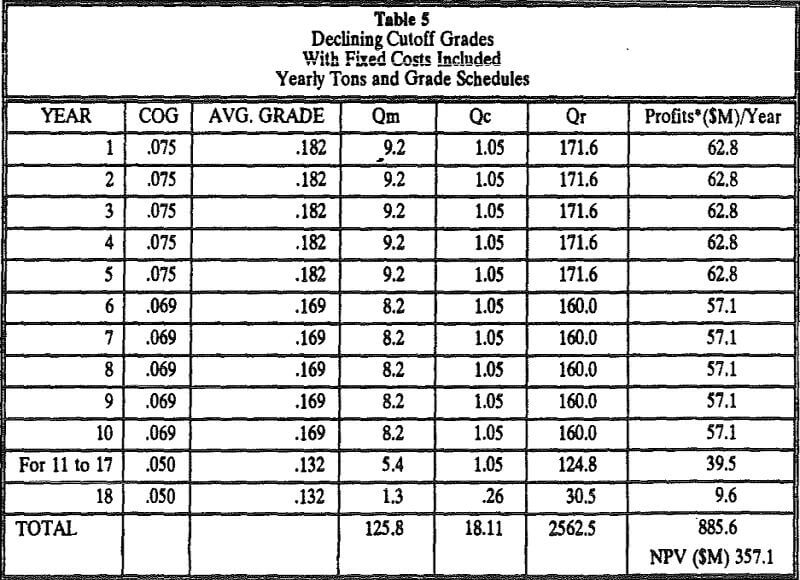
Table 5 gives yearly tons and grades schedules resulting from the cutoff grade policy that includes fixed costs as part of the cutoff grade and the profit calculation.

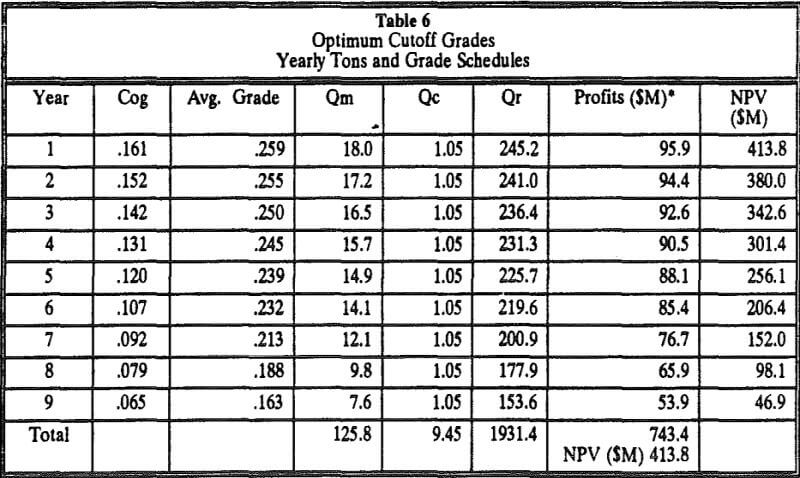
Optimizing The Cutoff Grades By Lane’s Approach

The preceding discussion has demonstrated the significant impact of the cutoff grade policy on the NPV of a project. It is generally accepted that the cutoff grade policy that gives higher NPV’s is a policy that uses declining cutoff grades throughout the life of the project.

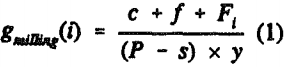
Where i = 1, N (mine life), gmilling,(i) is the cutoff grade to be used in Year i. The Fi is the opportunity cost per ton of material milled in Year i and it is defined as:

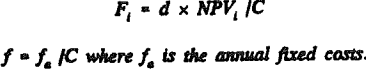
Where d is the discount rate; NPVi is the NPV of the future cash flows of the years (i) to the end of mine life N; and the C is the total processing capacity in Year i.

Algorithm for Determining Optimum Cutoff Grades

The cutoff grades gmilling(i) given in Equation (1) depend on estimates of NPVi of the future profits in year i through the end of mine life from the operation and NPVi of the future profits cannot be calculated until the optimum cutoff grades have been decided.

It is shown in this paper that returns on investments can be improved by exploitation of a deposit through optimum cutoff grade policy. It is also shown that the use of traditional cutoff grades in some cases will give sub-optimal NPV for a given deposit to an extent that the deposit can be rejected. I believe that only through the use of optimization techniques like the one presented here the accuracy of the decisions with respect to major mining investments can be assured.