Distributed Component Comminution Model

The general form of the comprehensive distributed component comminution model has been described as follows

d/dt(m(t)) = – [I – B]S m(t) = A m(t)…………………………………………..(1)

Where A is the fundamental matrix/state companion matrix or the so-called mill matrix in comminution literature.  The reason being that A as a general real matrix may have complex eigen-values and complex eigenvectors but more importantly, there is no guarantee that a set of eigenvectors of A will turn out to be independent.

Unfortunately e1+u = el . eu is true only for scalars but not true for matrices i.e. eL + U ≠ eL . eU unless they commute. In other words eAt = e(L + U)t = eLt. eUt ⇔ LU = UL. Since this is not the case, this decomposition scheme must be replaced by a mathematically acceptable method known as the “splitting method” (Trotter, 1959). The splitting method uses the “Trotter product formula” to approximate eAt as follows:

Where:

L is strictly lower triangular matrix
U is strictly upper triangular matrix and m is a large number which is known as Trotter parameter

For a general splitting A = B + C the approximation is:

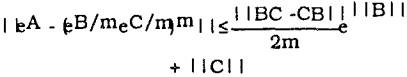
Results and Discussion

In order to demonstrate the validity of the computational procedure, an arbitrary real matrix having essentially the same characteristics as that of mill matrix A was chosen.

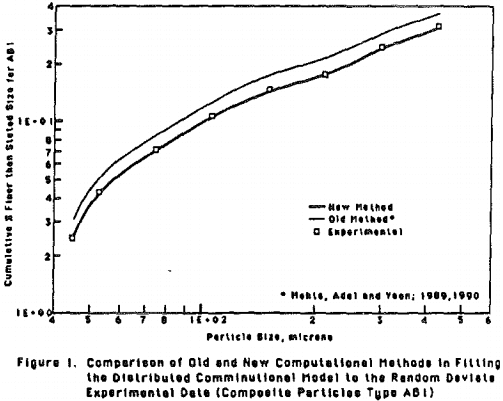
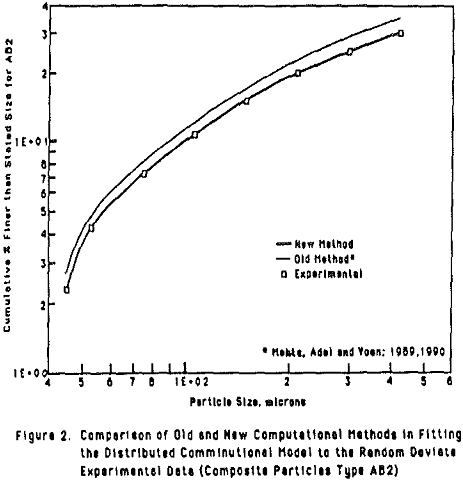
Comparison of Old and New Methodology in Terms of Model Fitting

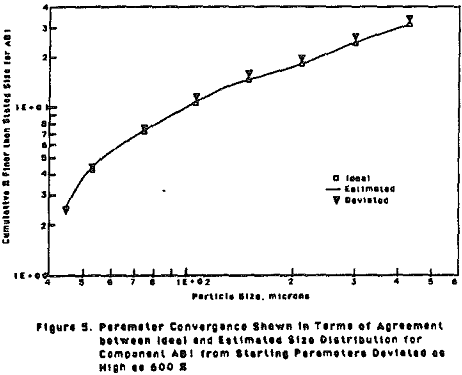
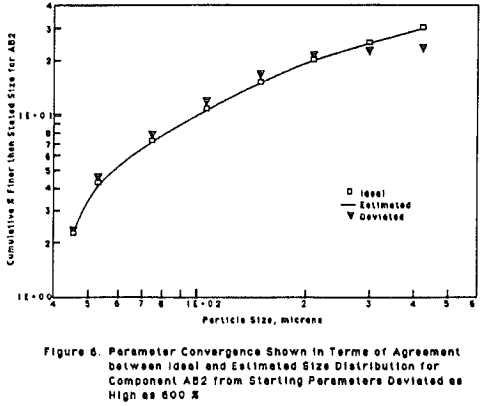
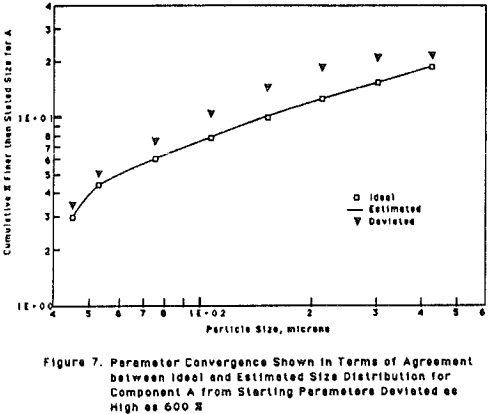
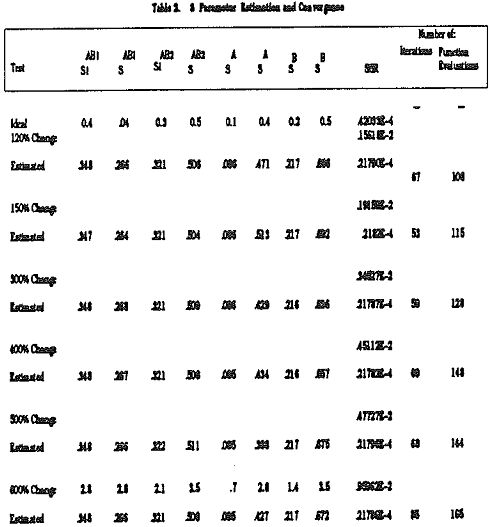
The novelty of the new method was demonstrated by considering a simple case i.e. binary model having two composite classes. The two methods (old and new) were tried independently on the same data.

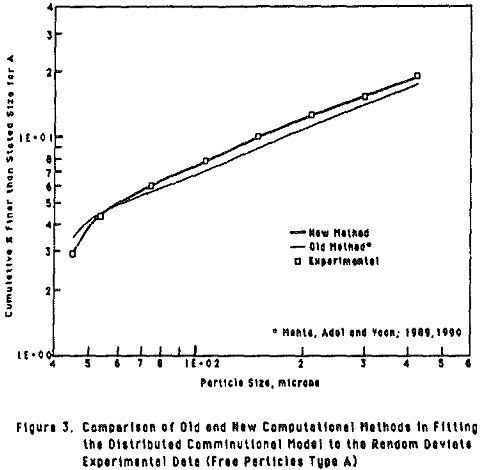
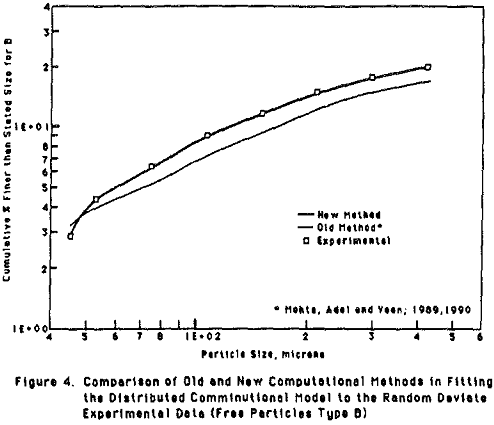
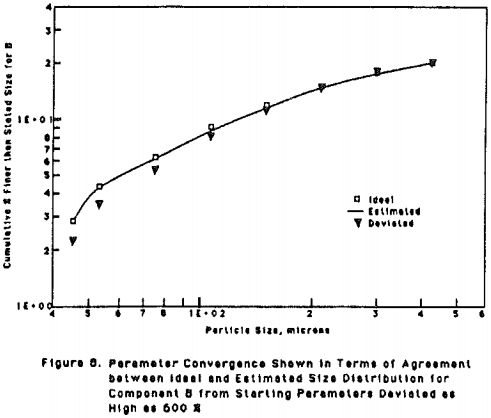
Parameter Estimation Utilizing Model Solution Computed by The New Method

A binary model with 2 composite classes was considered and estimation was carried out for S parameters. A set of true parameters (ideal) was used to simulate the multi-component system for t = 1, 2, and 4 minutes.