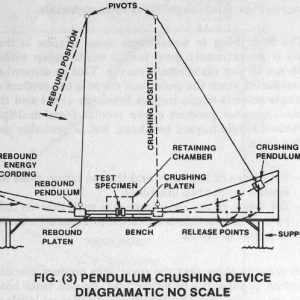
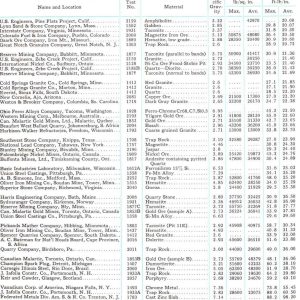
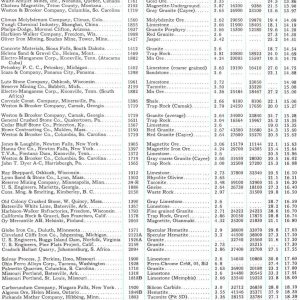
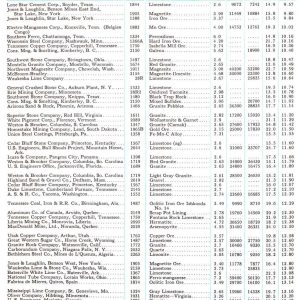
The Pendulum Tester / Bond Impact Crushing Work Index Tester.
Working principle Crushing by impact.
76 mm maximum feed size.
Test repetition: At least 10, preferably 20 test runs.
- Adjustable crushing angle
- Repeatable crushing results
- Safe two-hand operating buttons
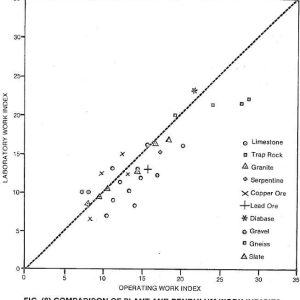
The Bond Crushing Work Index (CWI) describes the competency of the ore at larger particle sizes.
It is used for the calculation of the actual crusher power requirements.
- Pendulum mounted hammers with scale.
-Test: At least 10 specimens preferably 20 specimens to be tested. - Each broken stone has to pass a 3-inch square mesh and be retained on a 2-inch square mesh
- Two hand safety release for the impact hammers