The filter is an apparatus designed to hold the filter medium. At such a medium takes place the entire liquid-solid or gas-solid separation process. Hence, the medium is really the essence of filtration. Yet, the medium, an originally clean porous substance with trapped solids in it, is perhaps the most neglected part of filtration research.

Basically three problems prevail at the medium:

i) Penetration of solids and their blinding of the medium and the influence of such blinding on the resistance to flow.
ii) The behavior of the medium in long term repetitive filtration.
iii) The filter effect phenomenon whereby the flow rate on filtering an apparently clear liquid through a medium decreases with time.

The Fundamental Filtration Equation

All of today’s theoretical relationships for filtration are derived from D’Arcy’s law. It was published in 1856. Essentially, it relates the flow rate to the other parameters of the system. In a modified form this relationship is given as:

dV/dt = K AP/µL…………………………………………………..(Eq. 1)

where: V = volume of filtrate
t = time
K = permeability coefficient
L = thickness of bed
A = filter area
µ = viscosity coefficient

From the above relationship a fundamental filtration equation was derived by Carman. This equation includes a term Rm for the medium resistance.

dV/dt = PA²/µ(rvV + RmA)………………………………………….(Eq. 2)

where: r = is the specific filter cake resistance
v = volume of cake deposited by a unit volume of filtrate.

Upon integrating, the solution can be rearranged to give the form:

t/V = mV + constant.

which is the equation of a straight line. The slope m includes the specific cake resistance r and in determining the slope, a solution can be found for r. The constant term includes the resistance of the filter cloth which must indeed remain constant.

Filter Cloth Resistance

Filter cloth resistance is lowest at the beginning of the first cake forming cycle. If ideal conditions could be secured for a cloth then its resistance should remain at this level during its entire operating life. However, optimum conditions should be maintained somewhere in the range of the resistance of a clean cloth. If it were economically feasible and technically possible to discard the medium with each cake there would not be any problem with the resistance of filter cloths.

Repetitive use of a filter cloth will unavoidably result in the trapping of particles by the fibres. The purpose of the discharge cycle, besides removing the cake, is to dislodge the trapped particles and free the cloth from them before the next cycle.

 

 

 

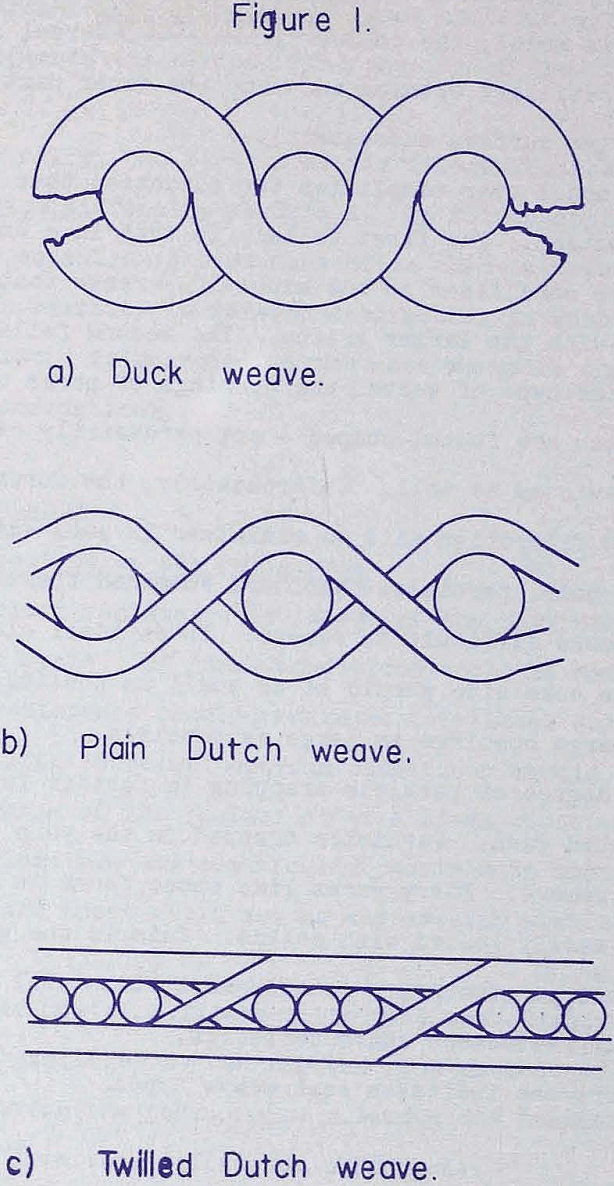
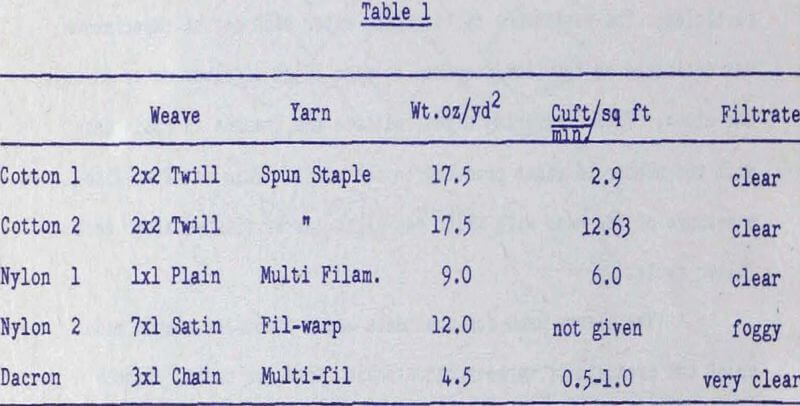
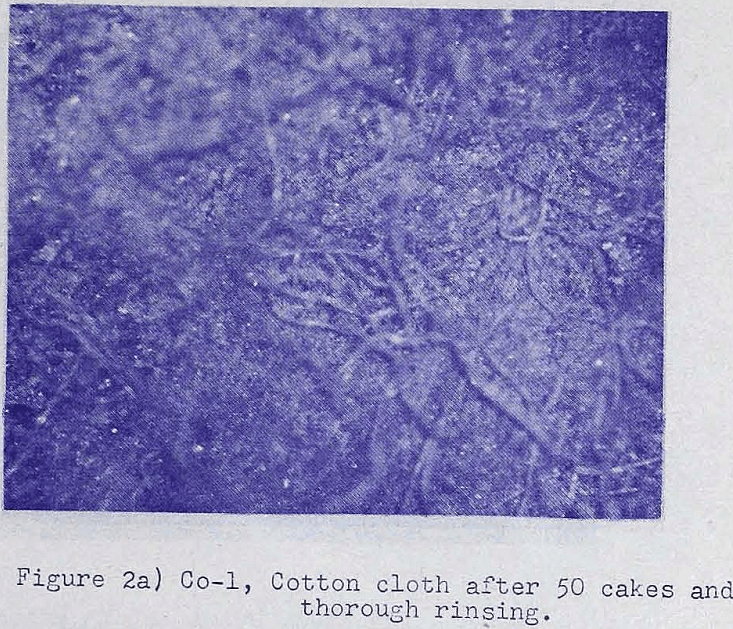
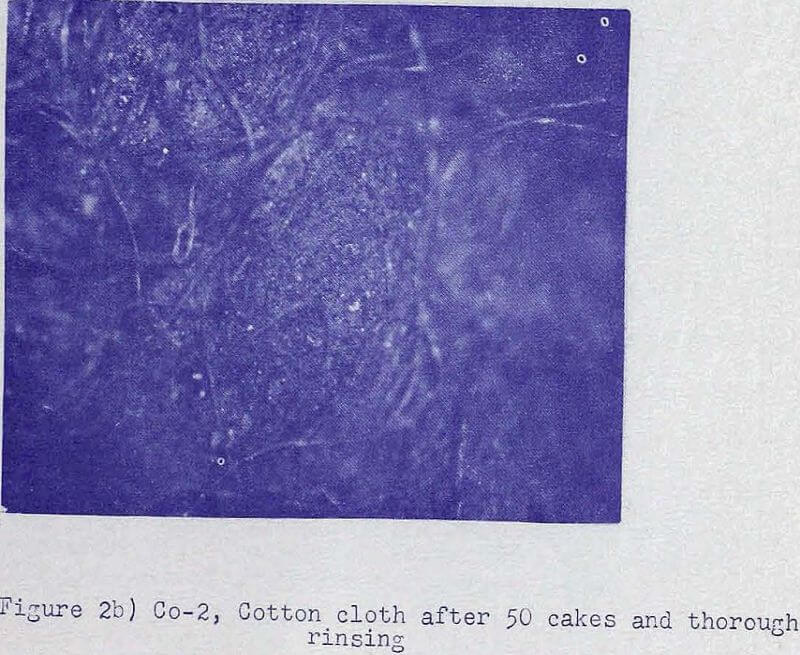
The Mechanism of Flow

The hydromechanics in porous media is concerned with the pore space of the medium, filled with the liquid. There are two aspects to be considered: macroscopic and microscopic.

The macroscopic aspect refers to the liquid as a continuous entity. The microscopic aspect takes the molecular structure of the liquid into account. This latter aspect is assumed to be of minor importance regarding continuous flow.

Fluids and solid surfaces also interact. This interaction is very important to the flow through a porous substance. Although the order of magnitude of these surface interactions is difficult to establish unanimously for a variety of materials, it is easier to appreciate its hindering effect qualitatively.

Theoretically 3 kinds of physical conditions determine the flow of a fluid:

1. The continuity condition,
2. The Theological equation of state,
3. Newton’s Law of motion.

This phenomenon must be now superimposed on the filter-cake-and-medium system. However, it should be noted here that such bubble development is not unique to hematite or to oxide ores. When the flow under vacuum begins through the channels and the voids of a filter cake, similar occurrence of bubbles will take place. The kinetic movement of the flow will shear these bubbles off and from that moment the flow will consist of a two-phase system. The situation has a certain physical resemblance to the streaming-potential phenomenon where charges are sheared off by the flow from the diffused double-electric layer.

The presence of the filter cloth with its trapped solids in the pores will represent the final obstacle in the way of the two- phase flow. At the cloth surface the permeability of the combined cloth-cake system will be at its lowest. The thickness of the cloth is, therefore, of great importance. Those bubbles that reached this region will have to move through the cloth. Fabrics woven of smooth, thin filaments can therefore permit a faster passage of such a water- bubble mixture than dense furry thick cloths.