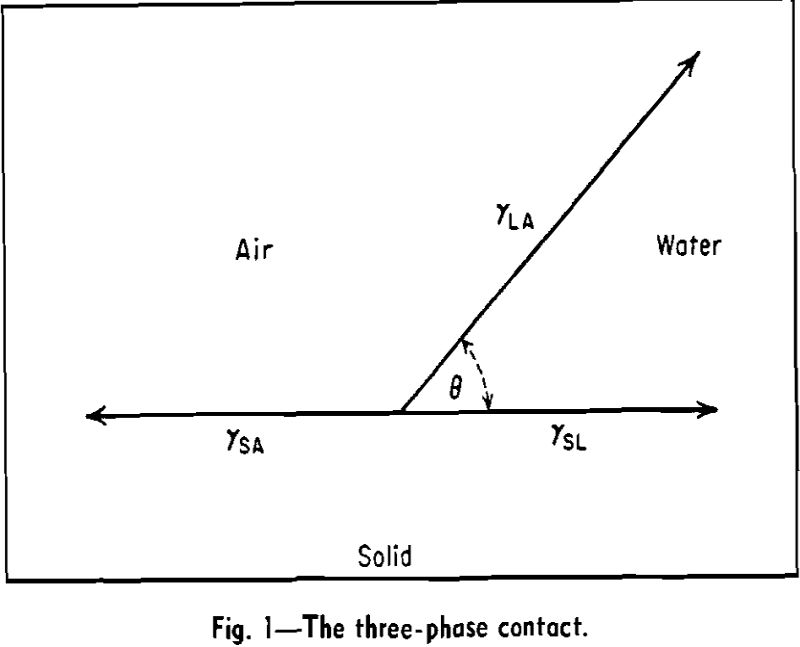
The technique of concentrating valuable minerals from lean ores by flotation depends upon the creation of a finite contact angle at the three-phase contact, mineral-water-air. If the mineral is completely wetted by the water phase, contact angle zero, there is no tendency for air bubbles to attach themselves to the mineral.

The contact angle is a complex quantity because the properties of three different phases, or rather of three different interfaces, control its magnitude.

γSA – γSL = γLA cos θ…………………………………………………………………[1]

According to this equation, the contact angle has one well-defined value. Actually it is found in many experiments that the value of the contact angle depends on whether the air is replacing liquid over the solid (receding angle) or the liquid is replacing air (advancing angle). The receding angle is always the smaller of the two.

A quantitative relationship between the surface tension or interfacial tension and the adsorption occurring at a surface or an interface is given by the Gibbs equation, which for constant temperature and pressure reads

where dγ is the infinitesimal change in surface tension accompanying a change in chemical potential

dµi, of the component i of the system and Γi is the number of moles of component i adsorbed per cm² of surface.

In dilute solutions, the chemical potential of a solute is given by the expression

µi = const. + RT ln ci…………………………………………………….[3]

where R is the gas constant, T the absolute temperature and ci the concentration of component i in the bulk solution.

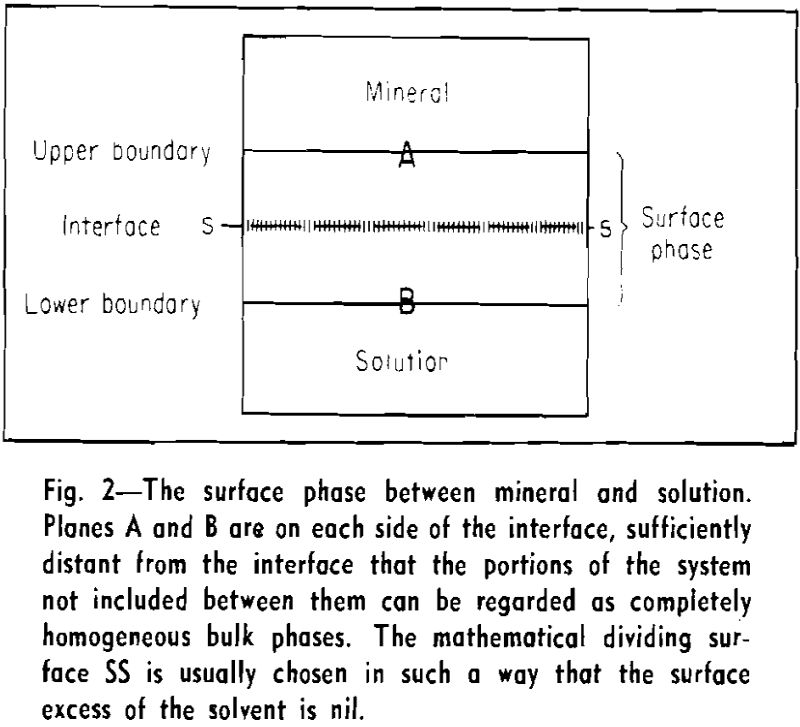
Gibbs pointed out in his fundamental treatise that the adsorption of any one substance cannot be defined in an absolute way. The adsorption of one chemical species can be expressed only in terms of that of another species. The amount adsorbed (Γi) may be defined as the excess amount of substance i present in the surface phase, that is, in the interface (or surface), plus the adjacent regions of the bulk phases.

is valid, where ni, is the number of moles of component i per unit volume. It is therefore immaterial where the mathematical dividing plane is placed or how much of the bulk phases is considered to belong to the surface phase.

Application to Flotation: Flotation systems usually contain such a large number of components that writing down the complete Gibbs equation for them, though not impossible or even difficult, would be tedious. Fortunately, in most cases what happens during simultaneous changes of all the chemical potentials is not of interest, but rather the effects produced by the addition of a single substance (collector, activator or depressant) to the system.

Influence of the Collector. A Simple Collection System: First to be considered is the addition of a collector that does not give rise to any chemical reactions or precipitations of insoluble phases. The solution already may contain any number of solutes which may or may not be adsorbed at the surface, but the concentrations and chemical potentials of these solutes will be kept constant.

If the collector is a neutral molecule, X, the Gibbs equation for addition of the collector would be

dγ = -Γ’x dµx — ΓH2O dµH2O…………………………………………….[5]

On the other hand, if the collector is an electrolyte, say C+X-, where X- is the active collector ion and C+ an inorganic cation like Na+, H+ or NH+ the Gibbs equation will contain three terms,

In Eqs. 5 and 6, the last term, ΓH2O dµH2O, is zero, if the convention is used that the adsorption of the solvent (ΓH2O) is zero.

In all cases of flotation, the collector is positively adsorbed to the mineral. This means that Γx or Γx- is a positive quantity if ΓH2O is considered to be zero. C

The conclusion is apparent, therefore, that in the collector system considered here the increase in contact angle has to be explained by a decrease of the surface tension mineral-air (γSA), a decrease which has to be larger than the decrease in γSL.

Precipitate Formed by Collector. A More Complex System: Analogous conclusions are reached in the somewhat more complicated system where the collector ion forms a precipitate with one of the ions furnished by the mineral.

For the process of adding collector to this system the essential form of the Gibbs equation is

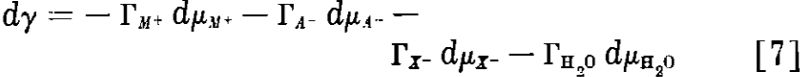
When both M+A- and M+X- are present as solid phases, the constancy of the solubility products can be expressed:

dµA- = – dµM+ = dµx-…………………………………………..[8]

With the assumption of zero adsorption of H2O, Eq. 7 then becomes

and with the condition of neutrality of the surface dy = (IV l\’a+) dfix- [10]

Activation: An activator is a solute which promotes the flotation of a mineral by a collector which otherwise would have no effect on the mineral. A generally accepted explanation of activation is that the activating ion is adsorbed on the mineral and acts as a bonding agent between the mineral and the collector.

If chloride adsorption is negligible (ΓCl- = 0) or if initial chloride concentration is large enough that the activator addition causes no appreciable change in chemical potential (dµcl- = 0), and if the convention ΓH2O = 0 is used, the Gibbs equation for activator addition simplifies to

Thus, for this simple system in which it is postulated that no precipitation or other side reaction occurs, the addition of activator lowers the surface tensions of the solid.

A common characteristic of activator-collector pairs is their tendency to react metathetically to form highly insoluble precipitates, and flotation has been observed under conditions where such reaction products are present. For the system in which the collector Na+X- and the activator Z+Cl- react to form a precipitate ZX, the equilibrium of the solution with the precipitate requires that

The Gibbs equation for addition of activator to this system then becomes

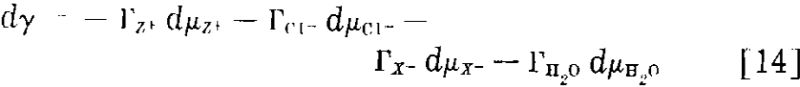
Omitting the terms for Cl- and H2O for reasons given earlier, and combining Eqs. 13 and 14

If the activating ion has valence n and forms with the collector a precipitate ZXn, Eq. 15 would become

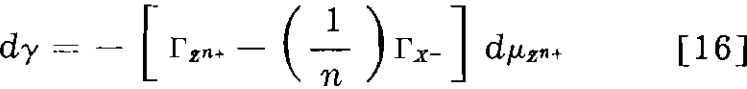
Eqs. 15 and 16 show that the direction of change of the surface tension on the addition of activator depends on the number of equivalents of activator and collector adsorbed.

Lack of Equilibrium at the Solid-Air Interface: Even if the mineral-solution interface reaches equilibrium readily, equilibrium is not necessarily reached at the mineral-air interface.

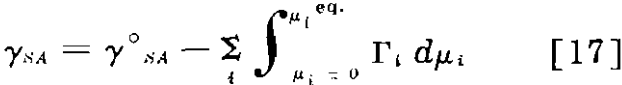
where γ°SA is the surface tension of the surface in the absence of adsorbing solutes (µi = 0) and the integral is supposed to follow only equilibrium conditions.

 

W. E. Ewers (Commonwealth Scientific and Industrial Research Organization, Melbourne, Australia)— Any attempt to elucidate further the meaning of the contact angle, particularly if it deals with the magnitudes of those mysterious quantities γSA and γSL, is certain to receive attention from those interested in the fundamentals of flotation.

Their Eq. 5

states correctly the relationship between the change in surface free energy dγ, the surface excesses Γx and ΓH2O of the components x and H2O and the changes dµx, and dµH2O in the chemical potentials of these components.

From this equation de Bruyn et al. correctly concluded that increased adsorption of the collector at the liquid solid interface would reduce the interfacial energy γSL. Their second conclusion, however, that an increase in the contact angle, corresponding to a greater decrease in γSA than in γSL, can be attributed to greater adsorption of X at the solid-air interface than at the solid-liquid interface is quite unjustified.

 

The equilibrium contact angle of the pure graphite measured under conditions designed to ensure that the surface had attained equilibrium with respect to the adsorption of water was 85.7°.

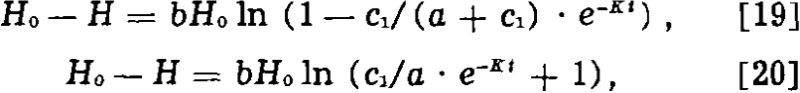
where H is the surface tension of solution, Ho that of pure water, t the time, c1 the initial concentration, K the time constant, α the concentration coefficient, and b the surface tension coefficient.

The relation between the surface pressure F and the surface concentration u was expressed as follows:

where R is the gas constant and T the absolute temperature.

Further, the relation between the surface pressure and the area S occupied by a gram molecule was expressed as follows:

FS/RT = FeF/bHo (eF/bHo – 1)……………………………………………….[22]

H cos x — Ho cos x0 = b’RT ln (c/a’ + 1)………………………………………[23]

where x is the angle of contact of solid against solution, x0 that of solid against pure water, and a’ and b’ are constants.

where B0 is the wetting tension of the surface not covered by gas molecules, Bi that of the surface perfectly covered by gas molecules, and B that corresponding to any fraction of the surface covered by gas molecules in a unit area of the surface, q1 the fraction of the area covered by the adsorbed molecules at the adsorption equilibrium, and n the time constant.

The Gibbs-Duhem relation for the solution phase, with all solutes at constant chemical potential except for the collector gives

where cx is the collector concentration in mols of X per mol H2O.

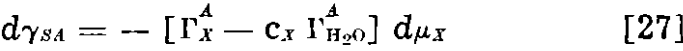
If we define Γx as (ΓAx – cx ΓAH2O), in which ΓAx and ΓAH2O are experimentally measured surface excesses in the gas-solid system, we obtain

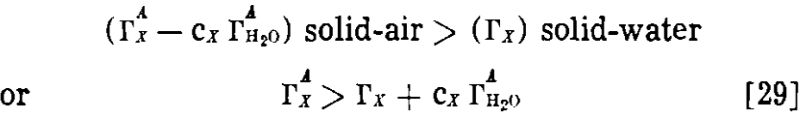
In other words, when the adsorption of water is taken into account, our case for a greater adsorption at the gas-solid surface is strengthened rather than weakened.