This paper reviews the progress made in testing the strength of rocks, ores, coal, salts, and other minerals as they are encountered in mine operations. It attempts to correlate the results of these physical measurements with technological properties more useful to the mining engineer: abrasive hardness, grindability, and behavior in comminution on one hand, and roof control, fracture of rocks in pillars, and mining methods with controlled caving on the other. In the following pages, the materials discussed will be referred to as rocks.

Basic Investigations

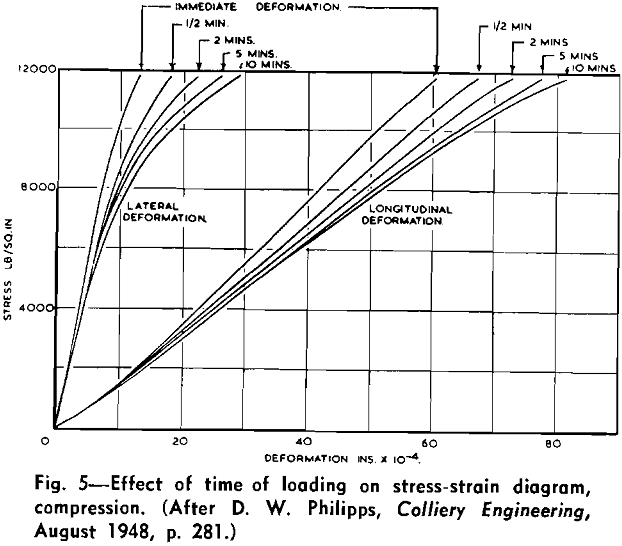
Historically, all work in the field has started with the simplest determinations such as those for crushing strength, abrasive hardness, and grindability. These serve the limited objectives in the researcher’s field of specialization: building construction, road ballast, roof control in mines, comminution, and seismic prospecting. Occasionally, fundamental properties like the modulus of elasticity E and Poisson’s ratio v have been determined with the idea that they might have some bearing on the technological properties of the material under investigation. But it was not until the work of Philipps, of Harvard University, and of the U.S. Bureau of Mines that sufficient basic data were collected to allow researchers to go beyond the technological test and find the fundamental laws behind the behavior of rocks in mine and mill operations.

The concept of strain-energy, expressed by Mr and represented graphically by the area under the stress-strain diagram, shows clearly the dependence of our rocks on the two variables, strength and elasticity.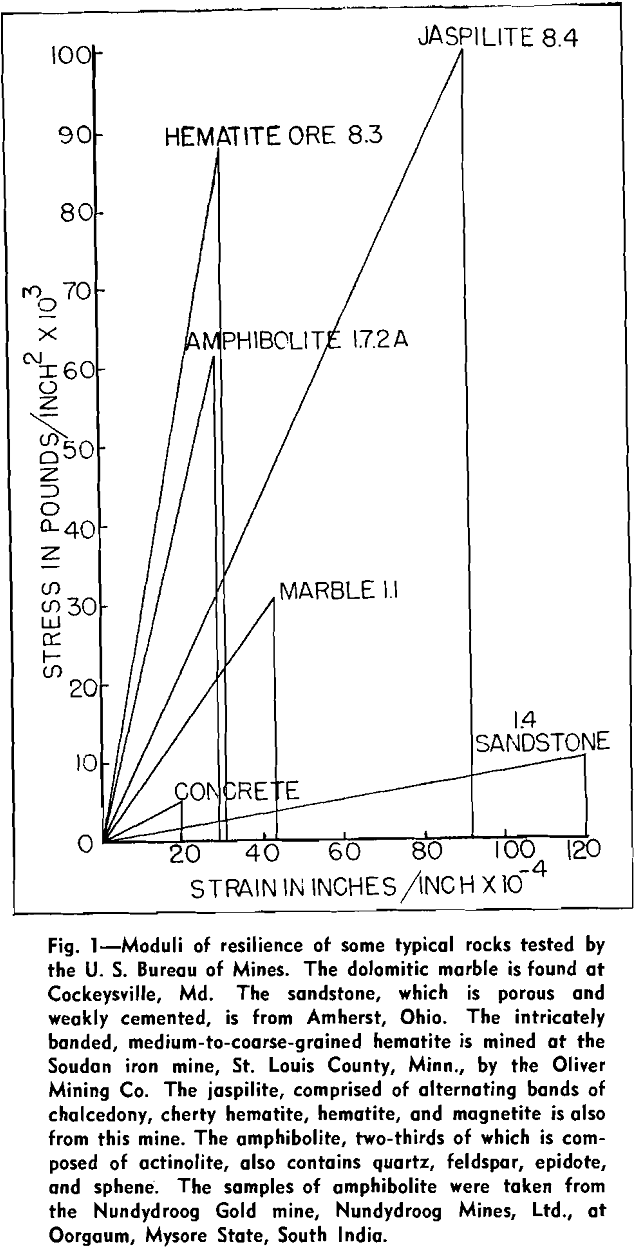

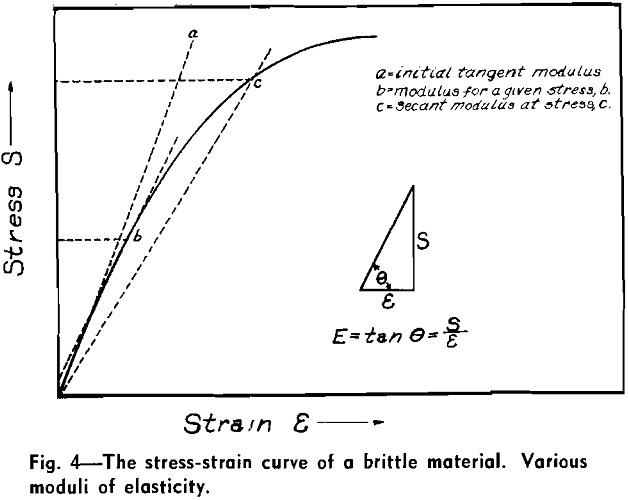
As it is difficult in this case to find a straight-line portion, or even the apparent modulus, concrete manufacturers, who have the most experience with such a curve, work with the following moduli of elasticity that can be represented by a straight line:

1. The initial tangent modulus. This is the line drawn as a tangent to the stress-strain curve through the point of origin,
2. the tangent modulus for a given stress, b, and
3. the secant modulus at a given stress, usually the proportional limit stress, if this point can be

found on the curve, or at any other assumed stress, c. This secant modulus of elasticity is the one most commonly used in design. As it is always less than the actual modulus of elasticity and less than the tangent moduli, it is also the safer one.

Applied Investigations: Relation Between Basic and Technological Properties

The fundamental physical properties discussed in the foregoing will in all probability be used only in the study of the problem of fracture of rocks. Their determination requires testing equipment that will be found only in universities and testing laboratories. Another disadvantage is that most tests (except the sonic) are destructive and require a greater number of specimens, leading to increased costs. Furthermore, a statistical average of a great number of tests has to be taken, as rocks do not possess definite properties. This is explicitly specified in the U.S. Bureau of Mines standardized tests. Here, in the case of compressive strength, it is recommended that the average of 10 determinations be used.

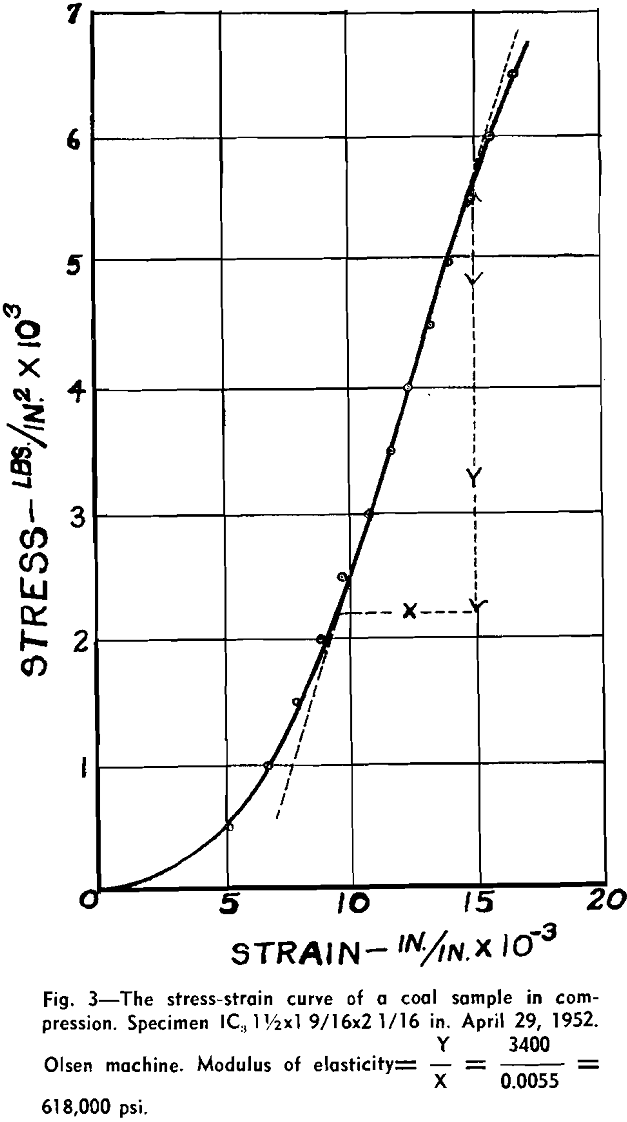
Correlation of Strength Properties with Density and Absorption

Most of the researchers quoted here have given correlations of elastic and strength properties of rocks with easily determined quantities like density, absorption percentage, or hardness. Correlation with density would be an ideal and most simple procedure, but in all the literature reviewed only one successful case has come to the writer’s attention. Kessler-Sligh in their investigation of the physical properties of limestones arrived at a straight-line expression for the ratio of compressive strength to density which is very impressive but which could not be found with any other rock. Limestone apparently is quite free of cavities, bedding planes, and other imperfections, and will give a fair straight-line expression.

Griffith has chosen a property closely related to density, namely, absorption. His argument is that “the physical behavior of rocks is conditioned much more by their relative degrees of molecular dispersion or states of aggregation than by their chemical constitution.”

Correlation of Strength Properties with Rebound Hardness

Better results are gained by the correlation of compressive strength with rebound hardness as determined with the Shore scleroscope. This too has been suggested by Griffith, and the value

So = 300 h ( 1 ± 1/10 )

has been given by him for the compressive strength (Sc) as a function of scleroscope hardness h for averages of the data rocks tested at the Iowa State College Engineering Experiment Station.

This correlation applied by the author to the group of more than 100 rocks studied by the U.S. Bureau of Mines gave better results than any other attempt. As can be seen from the curves on Fig. 6, the relation of compressive strength to scleroscope hardness can be fairly described by Sc = 400 hscler as average value. Griffith’s formula Sc = 300 hscler forms, with the rocks of the U.S. Bureau of Mines test series, the lower limiting value and Sc = 500 hscler the upper parameter, although the few extremely strong rocks found by the U.S. Bureau of Mines lie even beyond this formula. Some of the high strength values are not shown at all, as the ordinate does not extend beyond 50,000 psi.