The purpose of a surge bin between two machines is to permit either of the two machines to continue production for at least some of the time while the other machine is interrupted by break down or by preventive maintenance or by other problems up or down the line. This results in a higher capacity than would have been possible without a surge bin, particularly in the mineral industry where interruptions of production are frequent and long.

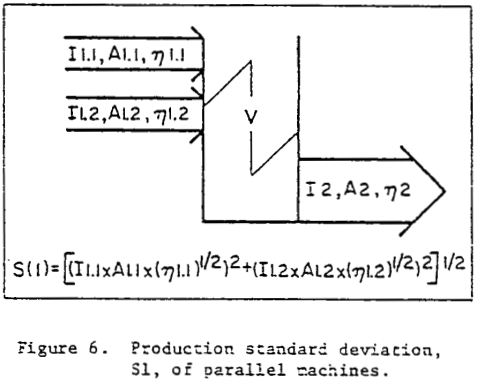
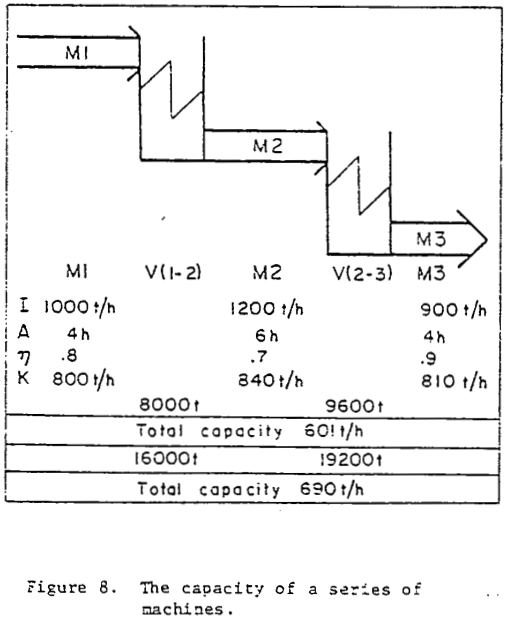
The machine 1 – surge bin – machine 2 – system

The ratio between the average length of production and the sum of the average length of production and the average length of interruption is the internal availability. The internal capacity is the product of rate and internal availability and would be the capacity of the machine if it operated between two very large bins and undisturbed of other machines.

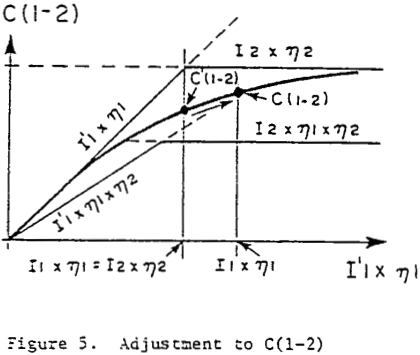
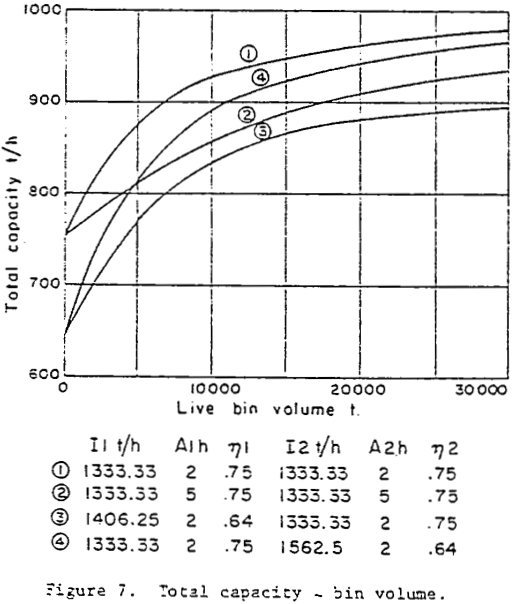
In a system with no surge volume between the two machines the ore moves ahead only when both machines are operating and only at the lower rate of the two machines rates. Installing a surge volume between them would result in an increase of production. At the limit, if a very large bin volume were installed between the two machines the total capacity of the system would approach the internal capacity of the machine with the lowest internal capacity. Intuitively one would expect that adding a certain bin volume to a small bin would result in a larger capacity increase than adding the same bin volume to an already large bin: the marginal benefit of adding volume decreases with increasing bin volume.

Production variation

The production of an isolated machine expressed in production per unit of time of operation varies from time to time. If the machine is producing continuously during the observed unit of time it obtains the highest production per time unit equal to the race. If it is stopped for preventive maintenance or broken down during the whole unit of observed time its production is nil. If production is interrupted or recommences during the observed unit of time, the production during that unit of time is somewhere between the rate and nil.

As production of the two machines vary so will the content of the bin. The content variation can be obtained by substracting the production of machine 2 from machine 1.

Under the assumption of equal internal capacities of the two machines the bin will be at an average ½ full and its content frequency function will be symmetrical. If the bin is very large the frequency function will tend towards 0 at both ends. If the bin is small the frequency function will be deformed at both ends, where the losses due to bin full or empty occur.

It has been found that sufficiently correct results will be obtained by assuming a rectangular or triangular bin content frequency function and carry out the integration at selected points. At figure 4 the principle of the integration is laid out. The loss starts when the bin content variation function passes above or below the limits of the bin.

The loss calculated following the development of the former paragraph is normalized and takes the value 1 when the bin volume is 0 and the value 0 when the bin volume is very large.

If in addition to the assumption of equal internal machine capacities it is also assumed that the rates of the two machines are equal, then the total capacity is the product of the rate with the two internal machine availabilities and with the loss factor plus the internal machine capacity multiplied by 1 minus the loss factor.