Table of Contents
A knowledge of the magnitude of the irreducible interstitial water in a porous medium is so important to petroleum engineering that its determination has become routine in core analyses.
In all geological formations there exists, in the pore spaces of the rock structure, water that is held in a state of equilibrium between capillary and hydrostatic forces. “Interstitial water” is the term given to this water and is defined as that water coexisting in the pore space with the oil prior to exploitation. The term “connate water” has often been used synonymously with this term; however, this can be true only by a specific definition since, geologically, it means the water in place at the time the rock structure was formed.
The basic definition of irreducible water is that water held in a state of equilibrium between capillary and hydrostatic forces. This water has been described by previous investigators as being held in the microcapillaries too small to support fluid flow. Actually, this fluid volume is made up of the water in the microcapillaries and as a film adhering to the surface of the crystals.
The actual mechanism of flow during desaturation is complex; however, it may be considered mainly as vapor migration by evaporation and recondensation on the multilayer film, resulting in a net loss by vapor diffusion to the drying air stream at the exterior of the sample. At the point of irreducible saturation, when the microcapillaries remain completely saturated, further migration of the meniscus results in only a small change in the adsorbed volume and the net loss in weight would be due to the evaporation of the multilayer film lining the larger capillaries. This rate of desaturation would be uniform for a short interval of time due to the approximate constant area and diffusion path.
As the evaporation proceeds, the constant rate of desaturation will decrease as the film lining the pores becomes less thick and the forces associated with the liquid-solid interface become more pronounced. The change in the rate of desaturation after the irreducible saturation has been reached will depend on the liquid and solid surface characteristics.
Follow rates of evaporation, the coefficient of diffusion friction or the change in vapor pressure with distance of diffusion inside the adsorbent is proportional to the mass of flow of vapor and a constant which is characteristic of the structure of the adsorbent. When this diffusing amount reaches the outer surfaces of the adsorbent it will be transferred to the air where the vapor pressure is P¹. The general equation combining the two diffusion processes, inside the adsorbent and from the surface to the air, is then:
Qm — K(Pv – P¹)…………………………………………………………….(1)
For practical purposes, with dry air blowing across the face of the sample, its vapor pressure P¹ in the atmosphere at a unit distance above the sample, will be small and may be neglected.
If the pressure on the liquid in the pores is exerted by virtue of the curvature of the meniscus, the relationship between the equilibrium vapor pressure Pv over the concave meniscus of a wetting liquid to the vapor pressure Po over the plane surface may be represented as a function of the radii of curvature by:

where δ is the surface tension of the liquid, M the molecular weight of the vapor, R the gas constant, T the absolute temperature, and r the radius of curvature of the meniscus.
The total volume of vapors V is then n V1 which is numerically equal to the pore volume less the liquid volume at saturation S1. A representative area for diffusion at S1 is V/L1 where L1 is the effective length of the capillary. The total mass vapor flow from the adsorbent is then:

If it is assumed that during desaturation equilibrium conditions are approximately maintained, then the combination of Equations (2) and (3) leads to a general relationship for mass vapor flow in terms of liquid and core characteristics:
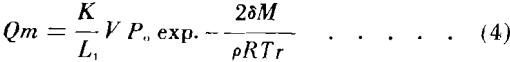
At the saturation representing irreducible volume, the change in V and r is small; K and L1 remain constant for a short interval of time such that the resulting rate of desaturation remains constant.
Experimental Procedure
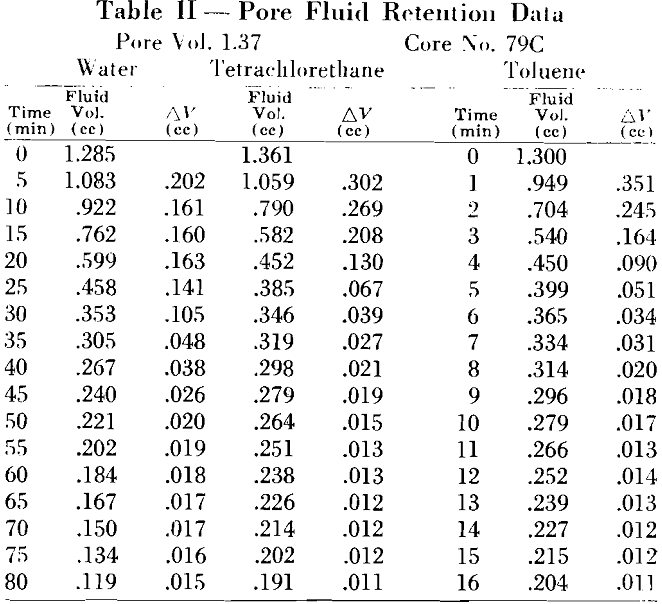
The evaporation method for determining irreducible water saturation is rapid and, in general, the experimental procedure consists as the name implies of evaporating the fluid from a saturated core until the rate of desaturation first becomes constant for a period of time. The fluid remaining in the core at the beginning of this constant rate represents the irreducible fluid volume.
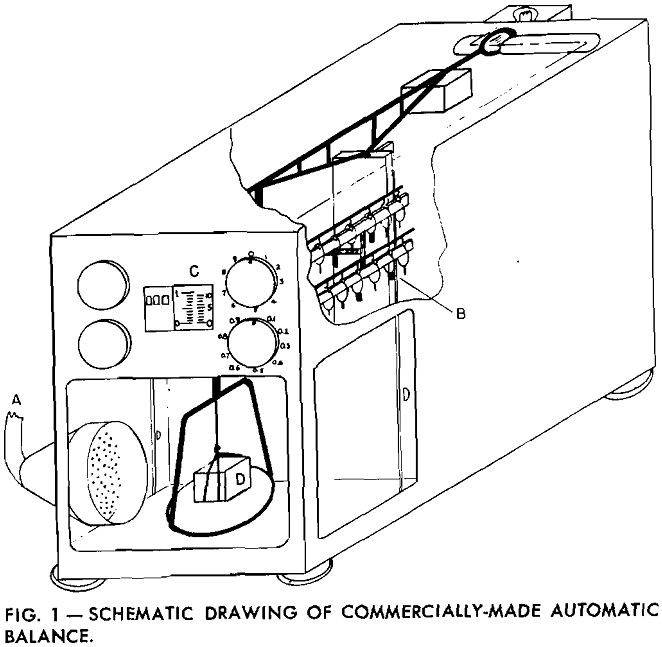
A stream of gas or air from A, passing over the sample, speeds the rate of evaporation and reduces the time interval for each test. An air flow of approximately 20 cfm was found satisfactory as it was not sufficient to agitate the balance and cause erroneous readings. During the experiment, weight readings were taken at equal intervals. These, transformed to fluid volume measurements, were plotted as a function of time.

An approximate magnitude of this volume factor can be obtained from the work on liquid adsorption by unconsoli-
dated material. It is realized that a volume factor thus determined may differ for consolidated material because of the added functions involved: however, the agreement in the experimental data indicated that either the added factors were negligible or compensating by their complexity.
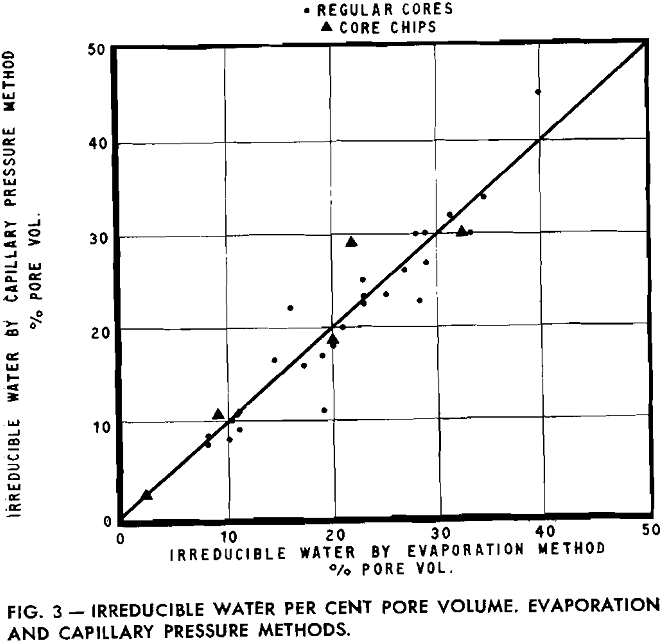
Experimental results obtained by the evaporation method were compared with measurements on the same sample by the capillary pressure method. Since this latter method has been evaluated by previous investigators, the comparison indicates that the evaporation method is a rapid means of determining irreducible water.
Capillary Pressure And Pore Radii
The role of capillary pressure has become important in the investigation of core characteristics and the values have been used by many authors to calculate pore size distribution and permeability. In the evaporation method previously described capillary pressures and pore radii are not a part of the data but a calculation of the trend in capillary pressures can be obtained by considering the vapor diffusion as represented by Equation (1). Capillary pressure and vapor pressure lowering are a function of the liquid saturation of porous media. A qualitative relationship between these functions can be obtained by considering the water and vapor as continuous phases in the system. If at any time the two phases are in equilibrium, the equation relating the vapor pressure above a curved surface with the capillary pressure is equivalent to Equation (2) and has been reported by Freundlich Calhoun and Lewis, Ledoux and others as:
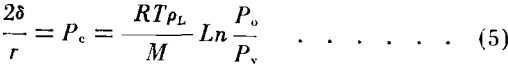
where pL is the density of the liquid.
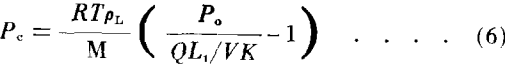
Equation (6) represents a general expression for capillary pressure in terms of vapor flow from the sample during an evaporation experiment.

Related: Best whole house water filters in 2022
