Table of Contents
The practice of the cyanide-process of gold-extraction has brought to light many important contradictions of familiar chemical analogies, which still obscure both the theory and the practice of the art with distinctions subtler and more difficult to make or follow than those which delighted the heart of the old-time metaphysician. Yet Nature herself has drawn these distinctions; and if we hope to succeed in this modern search for the Golden Fleece, we must be able to follow her through the winding labyrinth.
There are so many phases of this question that I shall attempt to touch on only one of them at this time, but it is one that lies at the root of many others.
In reviewing my paper on “ The Solution and Precipitation of Cyanide of Gold,” Mr. E. B. Wilson contends that “ in the solution of gold by means of alkaline cyanides the various reactions are determined, as to their order and intensity, by the relative position of the elements concerned in the electrochemical series, or series of voltaic tension.”
In a modified form this statement is probably true. That is to say, the difference of electrical potential in any closed electrical circuit determines the nature of the reactions which ensue. But the matter is not so simple as Mr. Wilson assumes. Recent investigations show that the order of the metals in the electrochemical series depends not only on the nature of the elements themselves, but also on the chemical composition of the solution in which they are placed; its degree of concentration; its temperature; and, in the case of gases, on the pressure.
Unless all these conditions are taken into account, inferences drawn from the electrochemical series are likely to prove more misleading than useful. The series, as quoted by Mr. Wilson from Gore, is as follows:

This series correctly shows the difference of potential in many solvents, especially in acid solutions, but the use of it for predicting the action of cyanide solutions involves several grave errors, one of which is the assumption that the nature of the solution in which substances are placed is without effect on the order of the series.
The remarkable effect of solutions of cyanide of potassium upon the relative positions of substances in the electrochemical series was first shown by Prof. Jacoby, who, called the attention of the St. Petersburg Academy of Sciences to the fact that when silver and cyanide of potassium solution replace the zinc and sulphuric acid in the Daniell cell, a strong current ensues and copper is precipitated. Ordinarily, and according to the usual inference from the above series, copper precipitates silver from its solutions; but here was a combination in which silver precipitated copper.
In the following year, Poggendorff announced that by his (now well-known) “ compensation-method,” he had found the electrochemical series in 1 part of KCy to 8 parts water—i.e., in a 12.5 per cent, solution of KCy, to be:

Gore also investigated this subject with similar results; only he showed that the order depends on concentration and temperature; and that, according to these conditions, gold may be more or less electro-positive than silver.
The variations thus discovered in the relative position of the metals in the electrochemical series at once cast a cloud on its usefulness for predicting chemical reactions; and though a great mass of experimental data was accumulated, and the most acute minds of the century were brought to bear on the problem, no explanation of these anomalies was found for many years.
It is only within the last decade that anything like a clue to the mystery has been detected; and this result has been made possible only through the combined efforts of a number of men who approached the subject from what may be almost termed its purely speculative side, without any thought of practical applications.
How that something tangible seems to be resulting from these efforts, I have thought that a brief outline of the rapid progress made in the electro-chemical theory during the last decade might be of service to those who have been too much occupied with practical details to follow theoretical investigations for themselves. Such an outline will also render more clear the bearing of the experimental work which follows.
Electrochemical Theory
Analytical Research
In the development of this subject, the efforts of investigation in the line of pure mathematics have been combined with the experimental methods of the chemist and the physicist with the happiest results.
Chief among the mathematicians in this particular held is Prof. J. Willard Gibbs, of Yale University, whose work is too little known and appreciated by his countrymen, or even by his own colleagues. His essays, published in the Transactions of the Connecticut Academy of Science, being purely mathematical, attracted but little attention in this country, but, being translated into German by Prof. Ostwald, were introduced to a public capable of appreciating them. He is now recognized in Europe as having anticipated many important discoveries with which Helmholtz had been credited. His predictions concerning the laws governing matter and energy have been verified as far as they have been tested, and are even yet far ahead of experimental verification. It is impossible to give here an adequate account of the work of this great man, but he will always be recognized as a leader in the application of mathematical analysis to the most profound physical and chemical problems.
Ions
While Gibbs and Helmholtz were busy with the mathematical side of the question, Daniell, Kohlrausch, Hittorf and many others were busy in following the experimental lines opened up by Faraday. Faraday had always assumed that the electric current was transported through a solution by discrete particles of matter, each bearing its own electric charge. To these moving particles of matter he gave the name of “ ions.” Those which move in the solution in the same direction as the positive electricity he called “ cathions,” and those which move in the opposite direction, “ anions.” The electrodes he distinguished as the “ cathode,” to which the cathions move, and the “ anode,” to which the anions move. These distinctions have proved of the greatest service; their value and meaning have been made yet more clear by the work of Daniell, and most of all by the classic experimental researches of Hittorf. The latter showed beyond question that the passage of the current was accompanied by an actual transfer of the cathions and anions through the solution in opposite directions. He and those who followed him were able to determine that these ions were sometimes simple elements, like sodium, potassium, silver, copper, etc., and at other times compound molecules like SO3, NH4, NO3, etc. Thus, while common salt would have for its cathion sodium, and for its anion chlorine, sodium nitrate would have for its cation sodium, and for its anion NO3. He proved these propositions by ingenious experimental methods which are still admired for their simplicity and certainty.
Hittorf showed also that, in the case of potassium argentocyanide, the principal cathion was not silver, but potassium, which alone traveled in the direction of the positive current. The silver traveled in the opposite direction, with the cyanogen and the negative electricity, and formed the anion (AgCy2). He explained the reduction of the silver which takes place at the cathode by proving that all (but a trace) is due to the secondary reaction which ensues when the potassium ion is deposited at the cathode and displaces an equivalent of silver from the silver cyanide there adjacent.
This experiment is so important that it will be considered more extensively below. It is sufficient in this place to say that he proved that, while an equivalent of silver was deposited at the cathode, the adjacent solution was robbed of that equivalent, and at the same time there was found an extra equivalent of potassium in the form of caustic potash, while about the anode there was an increase of one equivalent of silver and two equivalents of cyanogen. The conclusion is irresistible that the principle ions are, cathion (K), anion (AgCy,). He proved also that the ions migrate with different, moderate and easily measured velocities.
Molecular Conductivity
Meanwhile Kohlrausch, Ostwald and others were making a tedious and apparently useless investigation on the electrical conductivity of solutions of increasing dilution. The specific conductivity of dilute solutions is usually much smaller than that of more concentrated ones; but when the comparison was made on the basis, not of specific, but of molecular conductivity, a new and important law was discovered.
For the purpose of comparing the molecular conductivities of solutions, a unit known as the “ gramme-molecule ” was employed. A given volume v of solution is said to contain a “ gramme-molecule ” of a given substance whenever it contains a number of grammes of the substance equal to its molecular weight. Thus a “ gramme-molecule ” of potassium cyanide would be 65 grammes supposed to be dissolved in v liters of water. When v is one liter we should have a solution of one “ gramme-molecule ” per liter. In this case, for univalent substances, the “ gramme-molecule per liter ” is of course identical with one “ equivalent ” or a “ normal solution.”
Now, when we compare the total conducting power of a gramme-molecule of all electrolytes, we find that, as the volume v increases, and the solution becomes more dilute, the total, or molecular, conductivity of the whole volume of solution increases instead of diminishing with dilution, as the specific conductivity does. This increase is at first quite rapid; than the conductivity becomes nearly constant and increases only very slightly, to reach its maximum value for v = infinity.
Kohlrausch proved by a comparative study of these results that the total conductivity of a dilute solution is due to the velocity of the ions, and also that it is made up of the sum of the velocities of the cations and anions moving in opposite directions.
Osmotic Pressure
Meantime progress was being made in an apparently totally different field. Pfeffer, professor of botany at the University of Leipzig, made an extensive study of the osmotic transfer of solutions through the walls of plant-cells, and devised a method by which it was shown that osmotic action was capable of producing certain definite pressures. His method consisted in using a “ semi-pervious membrane ” through which the solvent, but not the solid in solution, can pass. When, for instance, a glass tube, closed at the bottom with a plug of porous earthenware coated with the semi-pervious membrane of ferrocyanide of copper, is filled with a strong solution of sugar and the lower end is placed in distilled water, the latter, being able to pass through the pores of the filter, does so; while the sugar particles, being unable to pass out, remain in the tube, and hence the solution column actually rises in the tube. Pfeffer showed that the pressure, as measured by the height of the column, was proportional to the amount of sugar in the solution and increased with the temperature.
The Gas-Law and Osmotic Pressure
These phenomena had long been supposed to be due to an attraction of the sugar for water; but the fact that the osmotic pressure was proportional to the sugar-content, and increased with the temperature, suggested to Prof. Van’t Hoff, the brilliant Hollander, that the dissolved substance acted just as a gas would do.
His reasoning was something like this: A dissolved substance exerts an osmotic pressure against the bounding surface of the liquid, just as a gas does against the walls of the vessel that contains it. But the surface of the liquid presses inwards with a pressure of above a thousand atmospheres (the Binnendruck of the Germans, which prevents the liquid from evaporating instantaneously into space). This surface-tension of the liquid resists the comparatively slight osmotic pressure, and ordinarily the latter produces no noticeable effect.
But when a semi-pervious membrane, through which water may pass, but which will filter out the sugar molecules, is interposed between the sugar solution and the clear water, the pressure of sugar molecules against the semi-pervious membrane and the upper surface of the solution raises the latter just as it would a piston; and as the sugar is unable to exert any pressure on the surface of the water on the other side of the semi-pervious membrane, the clear water freely enters the tube through the membrane as fast as the upper surface rises.
Of course, according to the gas-law, the osmotic pressure should increase with the concentration. Hence Van’t Hoff applied the gas-law, pv = RT, in which p represents the pressure, v the volume containing a gramme-molecule; T, the absolute temperature; and R, the “gas-constant.” When this formula was applied to Pfeffer’s results an almost perfect agreement was discovered; and the same result was obtained with numerous other solutions of organic substances. But when it was applied to inorganic salts, or electrolytes, it was found that the osmotic pressure was greater than that indicated by the molecular concentration. Van’t Hoff expressed this fact by the formula, pv — iRT, in which i is a coefficient greater than unity.
Here was an apparent anomaly; the osmotic pressure was apparently greater than that due to the number of molecules, that is, greater than the gas-law would indicate. Progress seemed to be stopped by a stone wall. But it was not delayed long.
Dissociation
Arrhenius, the masterly Swedish physicist, suggested a new idea. Perhaps the gas-law still holds, only the number of molecules has been increased by the dissociation of some of the dissolved substance. If a part of the molecules were supposed to be split, so as to double their number, the total number of molecules present would be increased and the gas-law might still hold. It was soon shown by Arrhenius that there was a close relation between the size of the coefficient i and the “ chemical activity ” of the substance. For instance, in the case of the inorganic acids, this coefficient was particularly large in those chemically most active, like hydrochloric and nitric acids. Assuming that in these cases the dissociation was most complete, he made another brilliant generalization. He distinguished between “ chemically active ” and “ inactive ” molecules, and claimed that the dissociated molecules were the only “ chemically active ” ones. This distinction has proved to be sound.
The next step was to show that the increase of molecular conductivity of dilute solutions was due to this same dissociation, and that the dissociated molecules alone took part in the transfer of the electrical current. Arrhenius concluded that the dissociated molecules formed the “ ions ” which Faraday had shown to be instrumental in conveying the current; that each dissociation produced a cathion which carried the positive electrical current, and an anion which carried the negative current in the opposite direction; that these alone were active in the electrical transfer; that when a substance was entirely undissociated it would he a non-conductor; and that its conducting power was directly proportional to the number of ions present.
This view was strongly contested at first. It was argued, in opposition, that such strongly combined substances as, for instance, potassium chloride, could not possibly split up in solution, even in part, into potassium and chlorine ions—that the potassium would decompose the water. But the reply was: “ What if it did ? The only effect would be to produce HCl and KHO ; these would again dissociate into H and Cl and K and HO; and the potassium and chlorine ions would still exist as before.” It was also suggested by Prof. Ostwald, of the University of Leipzig, that the ions were an allotropic modification, different from the ordinary elements, in that to the cathion was attached a positive charge, and to the anion an equal negative charge, of electricity; and that when these electrical charges were given up at the electrodes, the ions changed into the ordinary elemental form.
Ostwald was the first to defend these new views, and the position now held by the theory is largely due to his remarkable genius for outlining, executing and interpreting experimental work. Together with his students, inspired by his example, he has accomplished a great work in clearing up many difficult points as fast as they were raised.
Fig. 1 illustrates an ingenious experiment devised by Ostwald to show the bearing of the new theory. Two vessels, A and B, filled with a solution of KCl, are connected electrically by the column of solution contained in the siphon C. If the theory be correct, a large insulated conductor D, charged with negative electricity, and brought near the vessel A, will act by induction on the ions contained in A and B. The electrically positive, potassium cathions, will migrate through C and collect in A, being attracted by the negative charge on D. At the same time the electrically negative chlorine anions, repelled by the negative charge on D, will accumulate in B.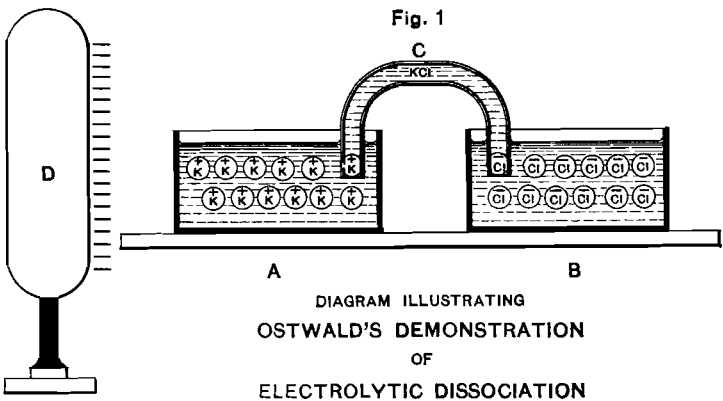
On removing C, so that A and B are disconnected electrically, and then removing D, the vessel A will contain an excess of positively electrified potassium ions, and the vessel B an excess of negatively electrified chlorine ions. So long as the vessels are not connected with each other or the earth, they will inductively remain in equilibrium and there will be no reaction between them. But according to the theory, if their contents be connected by a platinum wire, the potassium ions will give up their positive charge on the end immersed in A (hydrogen being set free by the reaction of the potassium on the water, as soon as the ions have given up their electric charge), and the chlorine ions will give up their negative charge on the end immersed in B (ordinary gaseous chlorine being similarly set free on that end of the wire).
The above experiment is difficult of actual execution on account of the enormous amount of electricity (96,540 coulombs) required by each gramme-molecule; but in a modified form of it, using a capillary mercurial cathode, Ostwald and Nernst were able to demonstrate the correctness of this view by traces of hydrogen, distinctly visible under the microscope.
Fig. 1 is therefore not so much a record of actual experimental demonstration as an ideal diagram, serving to explain the nature of the conception involved.
Altered Freezing and Boiling Points
Another important confirmation of the ideas of Arrhenius came from an entirely different quarter. It had long been known that the boiling point of an aqueous solution was raised and its freezing point lowered in proportion to its molecular concentration; and the method had even been used to determine molecular weights in cases of doubt. But here again dilute solutions proved an exception, showing variations in excess of what was due, according to the rule, to their molecular concentration. But when the behavior of dilute solutions was examined in the light of the new theory, it was found that the assumption of an increase by dissociation in the number of molecules present explained in these cases, also, the apparent anomaly. That is to say, when the rise of boiling and fall of freezing points of dilute solutions were expressed in terms of the total molecular concentration (allowing for the increase in number of molecules by dissociation, as determined by the method of electric conductivity), the observed facts accorded with the rule.
Heat of Neutralization
Another argument in favor of the dissociation hypothesis is furnished by the remarkable fact that the heat of neutralization of a gramme-molecule of all dilute acids is the same. When strong solutions of acids are neutralized with strong solutions of the several alkalis, the heat of the reaction per gramme-molecule is usually quite different; but when dilute solutions are used, the heat of neutralization per gramme-molecule is found to be practically the same for all the electrolytic salts.
This fact, inexplicable according to the usual views of chemical affinities, is a natural consequence of the dissociation-theory. The heat of combination in all these cases is practically equal to that due to the formation of a gramme-molecule of water—that is, to the combination of the atom of H in the acid with the molecule of OH in the alkali. The O and OH ions existing in water are infinitesimal in amount. Hence, when two solutions containing both in equivalent amounts are brought into contact, they unite, and the heat produced results from their combination. No heat results from the combination of the acid and alkali radical, because they were separated into ions before neutralization, and remain in the same state afterwards.
Hence, as the heat results solely from the reaction H2 + O = H2O, according to the new theory, it ought to be the same for all dilute solutions of acids and alkalies.
Solution Pressure
Professor Nernst, now of the University of Goettingen, made the next great forward step in explaining the anomalies in the electro-chemical series. He investigated very carefully the so-called “ concentration-cells.” The concentration-cell contains two electrodes of the same metal, each immersed in a solution of the same salt of the metal of its electrodes ; the only difference between the solutions being that one has a greater molecular concentration than the other. When such a cell is arranged like a Daniell cell (except that both electrodes are, say, of silver, one immersed in a normal, the other in a deci-normal solution of silver nitrate), and the electrodes are connected, a current of electricity results. From the electrode immersed in the dilute nitrate solution an equivalent of silver is dissolved, and at the same time on the electrode immersed in the concentrated solution an equivalent of silver is precipitated. The positive current flows from the electrode in the weak solution to that in the strong solution.
An electric current is thus produced from two electrodes of the same metal immersed in its own salt. Evidently, therefore, it can no longer be deemed necessary to have two different metals, or even the salts of two different metals, in order to produce a galvanic couple. But whence comes the electromotive force in this case ?
An attempt to answer this question led Nernst to propose the brilliant hypothesis which commonly bears his name and rounds out the modern theory of electromotive force. Briefly stated, it is that, for a given temperature, each metal has a certain definite “ solution-tension,” as he first called it, or “ solution-pressure,” as it has been more aptly named by Ostwald. According to Nernst’s idea, every metal immersed in a solution containing none of its ions possesses, at a given temperature, a certain “ solution-pressure ” with which its particles tend to go into solution and assume the ionic state. In doing this, each takes from the remaining metal a charge of positive electricity which it imparts to the solution. At the same time the remaining metal receives an equal charge of negative electricity. This causes the formation of Helmholtz’s “ double layer ” of oppositely electrified particles on the surface of the metal, and the process goes on until the attraction of the positively electrified ions for the negative metal just balances the solution-pressure of the metal. By reason of the enormous electrical charges of the atoms (96,540 coulombs to the gramme-molcule), it follows that only unweighable traces of the metal have to go into solution to bring about this equilibrium, which, once assumed, remains, unless a charge of positive electricity be imparted to the negatively electrified metal. When this is done, as happens when the circuit of a galvanic battery is closed, the formation of ions and the solution of the metal go on continuously. On the other hand, when a metal is immersed in a solution already charged with its own ions, these at once set up an osmotic pressure opposite to the solution-pressure, and hence, dependent on the concentration of the solution, there are three possible cases:
- The osmotic pressure of the ions already in solution may be less than the solution-pressure of the metal. Here the case is similar to the one described above, but the difference of pressure will be smaller than when no ions were originally present in the solution.
- The osmotic pressure of the ions in solution is exactly equal to the solution-pressure, and no double layer or difference of electrical pressure results between the metal and the solution. In this case the metal remains indifferent to the solution.
- The osmotic pressure of the ions already in solution is greater than the solution-pressure of the metal. In this case the ions in solution tend to precipitate themselves on the surface of the metal; and at the same time they impart their charge of positive electricity to the metal, which becomes positively electrified, while the solution which had contained an equal number of positive and negative ions becomes negatively electrified. This soon produces a new double layer of oppositely electrified ions, which brings about an equilibrium, unless a continuous stream of negative electricity is imparted to the positively electrified metal (as by completing the circuit of a galvanic battery), when the precipitation of the ions goes on continuously. The equilibrium of the double layer is brought about (for the same reason as given before) by the precipitation of unweighable traces of the ions.
According to this view, the electromotive force of a galvanic cell is just as much due to the difference of pressure between the metals tending to assume the ionic state, and the ions tending to assume the metallic state, as the force of a steam or compressed-air engine is due to the differences between the steam- or air-pressures acting on either side of the piston.
Hence, Nernst applied the laws of thermodynamics, which had been already worked out so thoroughly for gases, to this problem also, and with the most remarkable results. It is impossible to enter here into all the refinements of the subject; hut the following condensed statement will give an idea of the reasoning involved.
Starting with the well-known gas-law
(1) pv = RT
(p and P being pressures in grammes per square centimeter; V and v, the corresponding volumes in ccm. to contain one gramme- molecule; T, 273 + t degrees Centigrade; and R, the “gas- constant” = 1.96 calories), we can easily determine the maximum amount of work, A, in gramme-centimeters, done by a perfect gas, expanding at a constant temperature from a volume v to a larger volume V, and at the same time falling from a pressure P to a smaller pressure p. We have:
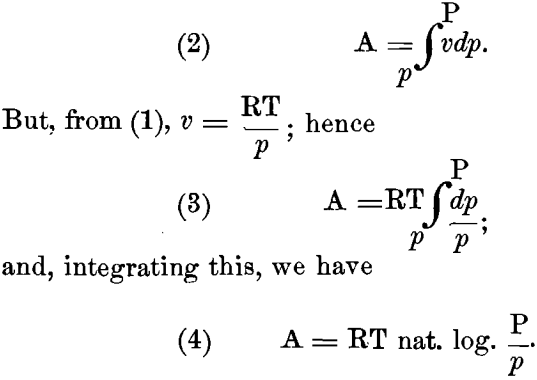
If we now suppose the gas-law to apply to the diffusion of the ions from the electrode into the solution; let P represent the “ solution-pressure ” and p the “ osmotic pressure ” of the ions of the given metal in solution; and further assume that work is done only in falling from the pressure P to the lower osmotic pressure p, and not in changing from a solution-pressure P to an equal osmotic pressure P, it follows that equation (4) will apply directly to this case also.
But we can also express the maximum work A in electrical units. If we assume that to a “ gramme equivalent ” of a univalent element is given its unit charge of e = 96,540 coulombs of electricity, and represent by the Greek letter the potential difference in volts between the metal and the solution, we may also represent the work A done, by the product π e. Hence we have:
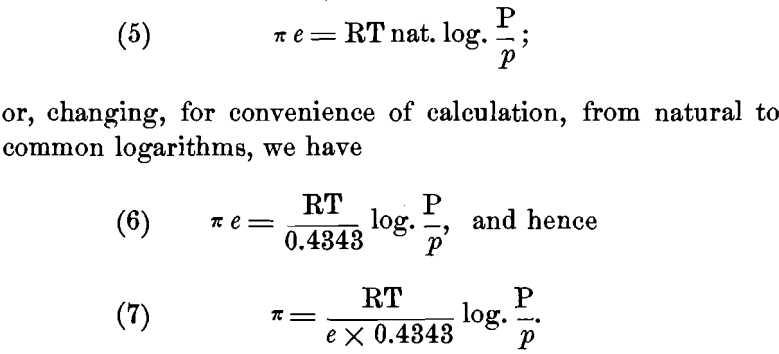
Now R = 1.96 calories, or, in electrical units, R = 1.96 x 4.24; e = 96,540 coulombs; and for ordinary temperatures t= 17° C. or T = 273 + 17 = 290° C. Substituting these values, we have:
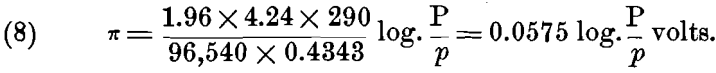
For ions that have a valency n > 1, each gramme-molecule will require n x e, or n x 96,540 electrical units, and this must be substituted in the formulas (5) to (8) instead of e; when this is done we have the general formula:
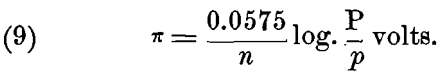
This formula, of course, is only true for t = 17° C.
I have plotted this curve in Fig. 2. It will serve for any metal in which the ratio P/p is the same. If we study the ratios of P/p we see that when P is greater than p, π always has a positive value; that is, the liquid is positively electrified by the ions which go into solution, and the remaining mass of metal is, in consequence, negatively electrified. As a further consequence, when p= 0, P/p = infinity; hence log. P/p, and hence π, equals infinity.
This, of course, is interpreted to mean that a metal brought into the presence of a solution containing none of its ions would have an infinite potential with regard to that solution; but this could only last for an infinitesimal period, after which the liquid would he impregnated with the ions of the metal. Experiment shows that none of the metals give an infinite potential in any known solution. It follows, therefore, that traces of the ions of all the metals must exist in all solutions, even though they may not be recognizable by any other chemical or physical test. The same mathematical difficulty exists with regard to the conception of a perfect vacuum, and a similar conclusion may be drawn, namely, that such a thing as a perfect vacuum is physically impossible.
When P = p, then P/p = 1, and log. P/p = 0. In this case, the potential is 0, and there is no tendency either to dissolve or to precipitate the metal.
When P is less than p, log. P/p is negative, and the solution is negatively electrified, owing to the positive ions precipitating themselves with their positive charges upon the metal, which becomes positively electrified. If p could become infinity, log P/p would become minus infinity. As a matter of fact, these values are never reached, for the simple reason that as p depends on the number of ions in a unit-volume, it follows that, on dilution, p reaches nearly a maximum value for very moderate dilutions, when dissociation of the liquid is nearly complete; and, after that, the value of p is reduced rather than increased by further dilution.
According to this view, the electromotive force of the metals in their solutions depends, for a given temperature:
- Upon the “ solution-pressure ” peculiar to each metal.
- Upon the number of ions of the given metal present in the solution in which it is immersed.
If the “ solution-pressure ” peculiar to each metal were accurately known, we might write out an absolute electromotive series for the metals. Le Blanc proposes, on the basis of the work of Neumann, and on the supposition that the osmotic pressure of a totally dissociated normal solution (containing one gramme-molecule in the dissociated state) is equal to 22 atmospheres, a series of this kind, as follows:
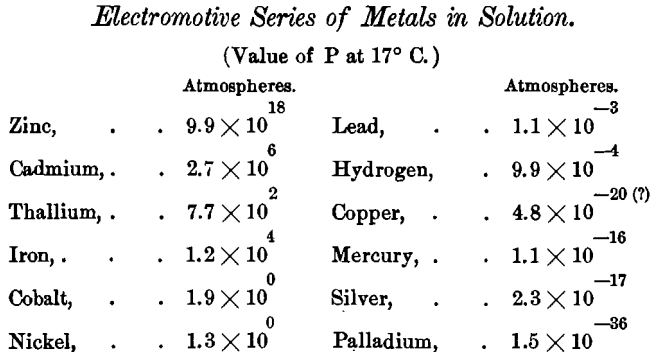
But it is in the varying number of ions present in solution that the true explanation of the apparent anomalies in the electromotive series was found. According to this theory the position of the metal in the series ought to vary in different solutions in accordance with the number of ions of the given metal that can exist in the given solution.
Complex Ions
The anomalous position of copper, gold and silver in cyanide solutions is here explained for the first time. According to this view, there are very few metallic ions of these metals in solutions of their cyanides. For example, the double cyanide of gold and potassium (potassium auro-cyanide) dissociates, in part, first into a positive ion K (+) and a negative ion AuCy2 (—). The latter, in accordance with the “ mass- law,” also dissociates, to a very slight extent, into AuCy (±) and Cy (—), and the AuCy, in accordance with the same mass-law, dissociates, to an almost infinitesimal extent, into Au (+) and Cy (—). The metallic gold ions, thus existing to an almost infinitesimal extent in cyanide solutions, are the only ones that exert an osmotic pressure against the solution-pressure of the gold. Hence, in spite of the low solution-pressure of the gold, the still lower osmotic pressure of the few gold ions present renders the potential of the gold in cyanide solutions remarkably high. Its solubility, also, is thereby explained.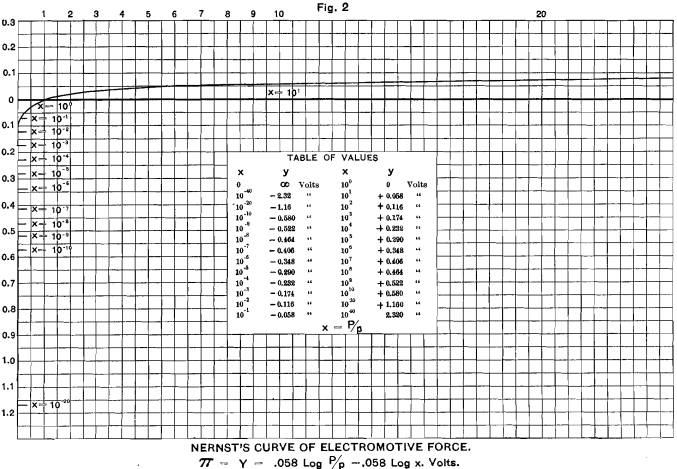
But a high potential difference does not necessarily indicate the great solubility of a metal; it may, in fact, indicate the opposite. For instance, the electromotive force of silver in cyanide of potassium solutions is high; but in sulphide of potassium solutions it is still higher—owing, in this case, to the extreme insolubility of the sulphide of silver. This extreme insolubility of the sulphide of silver reduces to a minimum the number of metallic silver ions that are present in the solution, diminishes the osmotic pressure of the ions, and hence increases the electromotive force.
The explanation of these remarkable exceptions that “ prove the rule,” is due to the work of Ostwald, who, more than any one else, has filled in the gaps and explained away the difficulties presented by the new views.
Beyond doubt, the gold, the silver and the copper in the cyanide solution are mainly combined with Cy2 to form electro-negative ions AuCy2(—), AgCy2(—), and CuCy2(—). As to silver, this conclusion is to be drawn, in fact, from Hittorf’s early experiments, and, as to gold and copper, from those of Ostwald, already described. These ions have been termed by Ostwald “ complex ions,” to indicate that they contain the metals in a combination in which their ordinary chemical reactions are entirely masked. There are many other such combinations: the thiosulphites of gold and silver, the ferrocyanides and ferricyanides, the platinochlorides, etc., all fail to answer the ordinary tests for the gold, silver, iron, and platinum that they contain. The alkaline sulphhydrates of many of the metals are also examples of the same fact.
It is for this reason that all of the ordinary reagents fail to precipitate the gold and silver from cyanide solutions. For this reason, also, the electric current causes a transfer of the electronegative ion from the negative to the positive pole, or anode, in the opposite direction to that ordinarily taken by the metals, and only the comparatively few electropositive gold ions present in the solution travel towards the cathode or negative electrode of the deposition-box. As already shown in my paper, just cited, this necessarily retards the electrodeposition of the gold from cyanide solutions. However, the potassium ions, on giving up their electric charge to the cathode, precipitate gold from the adjacent solution, and this helps matters out. Nevertheless, the travel of the AuCy2(—) ions to the anode considerably retards the precipitation of the gold.
To illustrate the great difference in the osmotic pressure exerted by the complex ions as compared with the ordinary case of dissociation, the following examples are cited from the work of Ostwald and his pupils :
Ordinary dissociation is represented by the cases of solutions of potassium chloride, copper sulphate, silver nitrate, and hydrochloric acid. These are found to be dissociated as follows:
KCl = K(+) +Cl(—) Practically wholly dissociated at M/10,000
CuSO4 = Cu(+) +SO4(—) Practically wholly dissociated at M/10,000
AgNO3 = Ag( + ) +NO3 (—) Practically wholly dissociated at M/1000
HCl = H(+) +Cl (—) Practically wholly dissociated at M/100
The above characteristic cases show that the degree of dissociation varies extremely with different salts, but with many substances, like silver nitrate and hydrochloric acid, is practically complete at very moderate dilutions.
Let us take in contrast the case of a complex ion, that produced, for instance, by the dissociation of potassium argento-cyanide. According to an investigation of Morgan, the dissociation takes place in three steps. Of these, the first is very complete:
KAgCy2 (±) = K(+) + AgCy2 (—)
(The latter is the “ complex ion.”)
The second occurs in very small amount:
AgCy2(—) = AgCy(±) + Cy(—)
The third is in almost infinitesimal traces:
AgCy (±) = Ag (+) + Cy(—).
In the case of M/20 KAgCy2, Morgan shows that the first step is almost complete; the second step is 2.76 x 10 -3 M = 5 per cent, dissociated; and the third step shows of Ag (+) ions, 3.65 x 10 -11 M = 3.65 x 108 x 1000 x 10 -11 = 3.94 x 10 -6 mg. per liter;—that is, there are only about four millionths of a milligramme of silver in the ionic state in a liter of such a solution.
Let us compare this with the dissociation in a M/20 AgNO3 solution. Morgan finds this to be 86.5 per cent, dissociated, hence a liter of such solution will contain 0.865 x 108 x 1000/20 = 4.36 x 10³ mg. of Ag(+) ions per liter.
The ratio of silver ions in the nitrate solution to those in the cyanide solution is therefore:
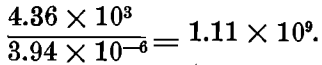
Hence, there are over a billion times as many silver ions in M/20 silver nitrate as in silver cyanide.
This makes clear at once the reason of the great difference between the osmotic pressure of the silver ions in the nitrate and in the cyanide solution, and consequently the reason why the electromotive force of silver is so much greater in the cyanide solutions. The case of potassium aurocyanide and other complex salts is entirely similar to that of potassium argentocyanide. It should be further stated that, according to this view, ions can only form or disappear in infinitesimal traces, sufficient to bring about a static equilibrium, unless they appear or disappear in pairs, positive and negative, as they do in the continuous passage of the current through the electrolytic cell. It is for this reason that it is necessary to have two electrodes to any galvanic cell, one to receive the discharge of electricity from the positively electrified cathions, and the other to receive that from the negatively electrified anions. Without both of these, a continuous current is impossible.
In considering this case of the Daniell cell, for instance: If we represent the solution-pressure of the zinc by P1, the osmotic pressure of the zinc ions present in the zinc sulphate by p1, and the similar values for the copper by P2 and for copper ions in the copper sulphate by p2 we shall have for the electromotive force of the zinc in zinc sulphate:
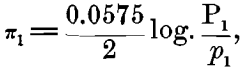
and for the copper in copper sulphate,
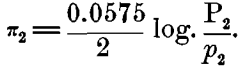
Either of these alone can give, not a continuous current, but only a static charge of ions, which prevents further action; but when they are combined on a closed circuit, as in the Daniell or gravity-cell, we have a resulting difference of potential:
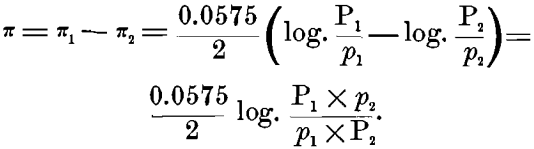
On the other hand, in a concentration-cell, with either of these metals (copper electrodes, for instance), one in a strong and the other in a weak solution of copper sulphate, we should have P1 = P2 in the above formula, and the only difference would be in the differing concentration of the ions p1 and p2 in the strong and weak solutions. Making these substitutions in the formula, we should have, in this case :
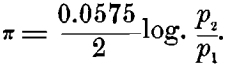
In this case it is evident that the solution-pressure of the metal itself plays no part in creating the electromotive force of the combination. It is entirely due to the relative number of ions present in the strong and weak solutions. The solution containing the smaller number of ions per unit-volume will oppose to the solution-pressure of the metal immersed in it the smaller resistance, and that metal will dissolve and the other will precipitate.
The above outline gives only in the briefest way a summary of some of the hardest thinking and closest reasoning that has been done of late in one of the most important departments of physical chemistry. It is, perhaps, too much to hope that the conclusions reached are all final. But they rest on such a firm foundation of experimental work, and explain so much that is otherwise inexplicable, that it is certain that they contain a large amount of truth. The details will probably be filled in quite differently from what we now expect, but the great mass seems to be solid gain. The importance of these new views in the study of chemical geology and the deposition of ores, in every branch of the metallurgical art and in all departments of practical chemistry, has hardly begun to be appreciated and utilized. It is not too much to say that ionic action lies at the bottom of all plant- and animal-life ; and that the new views are sure to create a revolution in the study of physiological chemistry, biology, pathology and therapeutics. In every department of physical science where they have been applied, they have acted like a new ferment; this speaks volumes for their usefulness and virility.
Electrolytic Theory
The above theories have not been received without opposition from many chemists and physicists of no little weight. Many of the first opponents to the theory have been overthrown, and point by point has been won against the strongest opposition. But the field is by no means clear of weighty objectors. The English school, led by Pickering with his “ hydrate theory,” has opposed most bitterly the new theory of “ dissociation.” Others, such as Crompton in England, and Bucherer in Germany, have proposed what may be termed the “ association ” as opposed to the “ dissociation ” theory. The battle still rages. While the issue seems certain in the main to be in favor of the new views, there is not wanting evidence of the wisdom of a compromise on certain minor but important points.
It will be noticed that the adherents of the dissociation theory neglect in toto the effect of the solvent. Formerly, Chemists fixed their eyes on the mystic power of the solvent to clear up any doubtful question. The new theorists ignore the solvent entirely. It is indeed astonishing what they have been able to explain without it, but, like Banquo’s ghost, “ it will not down.” They have assumed the solvent to be without action in bringing about dissociation and electrolysis. They have regarded it simply as of the nature of a vacuum into which the ions were free to expand, and everything has been supposed to be due to the pressure of the ions, nothing to the medium.
But already there are signs of reaction. It has been noticed that not all solvents are capable of changing salts into electrolytes. Some are almost without effect in this respect. In other words, not all liquids are capable of becoming vacua into which the ions may evaporate. This fact of itself is enough to show that the nature of the solvent is not without influence on the dissociation.
It was next noticed that most of the solvents which enable electrolysis to take place contain oxygen, and that of these, those possess the power most strongly which contain the most oxygen. Next, it was suggested that in all probability oxygen is quadrivalent rather than bivalent, as usually supposed. The fact that carbon, which is never known to be anything but quadrivalent, combines with oxygen to form carbon monoxide (CO), favors this view. If oxygen be regarded as at least potentially quadrivalent, an explanation is at once found for the well-known variations in the water of crystallization of salts; for Pickering’s remarkable series of “ hydrates;” and last, but not least, the idea suggests itself: “ May not the ions be, not merely a dissociation of the dissolved salt, but an association of the dissociated ions with one or more water molecules ?”
It was first supposed that all solvents capable of forming electrolytes contained oxygen. This was disproved by the discovery cited by Ostwald, that liquefied ammonia (NH3), a non-conductor, becomes a conductor when salts are dissolved in it. This was cited to prove that the ionizing force was not due to the presence of oxygen. But it was pointed out by Bruehl, that, like oxygen, the nitrogen in NH3 has two unsatisfied valencies, which are thus capable of acting like it in producing ionization. He predicts that anhydrous HCN when liquefied, as well as PCl3 and ASCl3, will be likely to have similar effects for similar reasons. Nernst has also called attention to the singular proportionality between the dissociating power of solvents and their dielectric constant. The latter are as follows for certain solvents :

This series might almost serve as showing the relative dissociating-power of these substances.
Thwing had also called attention to the remarkable difference of the dielectric constants between water and ice, that of water at 0° C. being 79.46, and that of ice at —2° C. being 3.36 only. He also gives 10.30 as the constant for liquid acetic acid, and 2.79 for solid. In all these cases, the dissociating power increased with the dielectric constant. This points to relations worth following to a conclusion.
It does seem, then, as if the adherents of the dissociation theory had ignored too much the effect of the solvent, and as if the final theory must be enlarged to include it. Why should the action of the solvent be ignored ? Its chemical action, it is true, is often slight, but when we take into account the effect (in dilute solutions) of its relatively great mass, does not this explain why dilute solutions are more dissociated than strong ones? In the latter, the cohesion of the solid still maintains, even in solution, a certain effect; but as the mass of the salt diminishes, and that of the solvent increases, the latter makes up by its mass what it lacks in intensity.
If the solvent is without effect, why does not the solution-pressure of the metals cause them to ionize as freely into a vacuum, or into the air ? And why should one solvent be effective and not another?
The dissociation-controversy in England waxed particularly warm in the numbers of Nature published.
One can hardly read this discussion without feeling that, on the whole, the dissociation theory has the better of it. But the associationists, led by Pickering, are not wholly wrong. Pickering cites one experiment that is worth quoting. He says that when a solution of propyl-alcohol in water is placed within a semi-permeable membrane, the water from without passes through the membrane into the interior. This seems to prove that the membrane is pervious to water but not to propyl-alcohol. But, he adds, when the same vessel is immersed in propyl-alcohol the propyl-alcohol passes in through the membrane, but the water cannot get out. This would seem to prove that the membrane was pervious to the propyl-alcohol but not to the water. He considers this a reductio ad absurdum. But Whetham points out that the experiment may be interpreted to mean that the membrane is pervious to either water or to propyl-alcohol, but not to their associated molecules or to the solution of one in the other.
Whetham also points out that the assumption that the ions are dissociated from each other does not in any way contradict the assumption that they are severally associated in some, as yet unknown, manner with the solvent.
Lord Kelvin (loc. cit, p. 273) takes an agnostic, if not skeptical, position. After stating the problem of osmotic pressure, he says:
“ No molecular theory can, for sugar or common salt or alcohol dissolved in water, tell us what is the true osmotic pressure against a membrane permeable to water only, without taking into account laws, quite unknown to us at present, regarding the three sets of mutual attractions or repulsions : (1) between the molecules of dissolved substance; (2) between the molecules of the water; (3) between the molecules of the dissolved substance and the molecules of the water.”
He follows this with a warning against undue haste in accepting theoretical views as settled while they are still open to debate.
On p. 461 (loc. cit.) Prof. J. Willard Gibbs shows that in the case cited by Lord Kelvin, for dilute solutions, where the relation of the density and pressure of the dissolved substance becomes like that of a gas, it is only necessary to have a single numerical constant in addition to the relation between the density and the osmotic pressure to solve the problem.
It must be remembered that the greatest triumphs of the new theory are confined to dilute solutions, but a complete theory of solutions must, of course, include all states from the dilute solution through the saturated solution to the solid substance with its various hydrates.
In describing the condition of affairs assumed in the new theory of ionic dissociation, Le Blanc says :
“ The parts resulting from the dissociation (the ions) are electrically charged, and contain equivalent amounts of positive and negative electricity. It is natural to ask: Whence come these sudden charges of electricity ? They seem to be produced from nothing. An answer that seems satisfactory is not difficult to give. It is known that metallic potassium and iodine combine to form potassium iodide. In this combination heat is generated, which shows that the two have entered into a state in which they contain less energy than before. A certain amount of chemical energy doubtless still remains in the compound, and when the salt is dissolved in water, the greater part of this chemical energy is changed into electrical, through, the influence of the solvent. This is the energy seated in the charges of the ions. The potassium ion is positively, and the iodine negatively electric. By the aid of the electric current, it is possible to add to these ions the energy in the form of electricity necessary to give them the energy they originally possessed as elements. In such a case, they separate in the ordinary molecular forms at the electrodes.”
It will be noticed that in this explanation of the mode of formation of the ions on the dissociation hypothesis, Le Blanc uses the phrase: “ through the influence of the solvent.” That is, he seems to recognize the need of bringing this influence into the problem. He does not attempt to show how it acts. But if it is able to alter such strong affinities as those of potassium and chlorine, or even of potassium and iodine, by changing the chemical into electric energy, such action is surely worth studying most closely.
I am firmly convinced that the next great advance will be made when the effect of the solvent is more closely studied. But while believing that the association or loose combination of the water-molecules with the dissociated ions plays an important, though as yet unknown, part in electrolysis, I shall, in what follows, continue to use the method of nomenclature already in use for the ions, in the absence of a better system.
