Trends in extractive metallurgy in recent years from milling and smelting of high-grade ores toward heap leaching and electrowinning of low-grade or marginal ores, have resulted in increased reliance on solvent extraction as a key part of profitable operations. Consequently, solvent extraction processes and reagents have been extensively studied, resulting in greatly improved techniques and extractants. Solvent extraction modeling, which predicts extraction under various conditions, has been used as a tool by researchers and some industrial chemists to decrease the number of time consuming and laborious shake-out tests needed to produce data to operate effectively the extraction unit. Modeling of nickel extraction from ammoniacal solutions was the goal of this work.

Often-cited earlier modeling work centered on copper extraction from acidic solutions with chelating hydroxyoximes. A statistical model of copper-ammoniacal systems was developed by Valdes using very high concentrations of aqueous copper. Establishment of extraction mechanisms and development of appropriate equations for ammoniacal systems was done with copper and nickel by Cooper and Rice. The work of Cooper was in some ways similar to this report in that he predicted copper and nickel extraction using LIX 64N with only a 6-pct error. However, some important aspects were not considered or reported. No equations were given for the prediction of other extraction governing quantities such as NH4+, free NH3, SO4²-, or pH. The origin of some of the equations was left unclear, and the metal to extractant ratio was higher than might be expected in industrial situations. Rice developed an excellent theoretically based equation for the prediction of nickel extraction from ammoniacal solutions. His work was done under idealized conditions at relatively dilute aqueous nickel concentrations and using only a single extractant concentration. The possible use of his derivation methods or equations for metals other than nickel, such as copper, was not attempted.

Some proposed nickel processes use an ammonia-ammonium carbonate leach, other processes produce ammonia-ammonium sulfate leach liquors. Modeling these types of systems is much more involved than for acidic systems, due mainly to the fact that there are additional ammonia complexes to identify and the resulting equations are increasingly complex. Brown developed a thorough model for an ammoniacal-carbonate system, but gave no extraction constants and only briefly described the model. He reported on only a single extractant at a fixed concentration. Agarwal discussed a major influencing factor, the effect of free ammonia on extraction efficiency.

A model that began with a limited number of starting conditions and accurately predicted not only the metal (copper) loading concentration, but also the concentrations of other species, including free NH3, organic NH3, and metal concentration in raffinates, and pH and metal coordination numbers, was developed and reported by Nilsen of the U.S. Bureau of Mines. The model worked well over a wide range of operating conditions for both ammoniacal sulfate and carbonate systems, and for extractants LIX 64N and P5100.

The Bureau, in an endeavor to expand the knowledge and improve the processes of solvent extraction, initiated a research project that would produce a nickel prediction model similar to the previously mentioned copper model. There is little other reported work on nickel, and that is usually centered on prediction of only nickel over a narrow range of conditions. The Bureau sought to develop a versatile model that would predict several influencing quantities such as: raffinate NH4+, pH, Ni, free NH3, coordination numbers, as well as nickel loading on the organic. Adapting the successful copper modeling techniques to the nickel data would not only decrease the time needed to develop a complete new model, but would show the adaptability for this type of model. Nickel sulfate and carbonate systems were studied using LIX 64N and P5100, with extractant concentrations ranging from 1 to 25 pct. All data were obtained for equilibrium conditions at 25° or 40° C. Development of an acceptable level of prediction was more difficult for the nickel systems, due partly to the fact that nickel has more and higher coordination numbers. This report is meant to be a companion report to the copper report and is intended not only to broaden nickel extraction knowledge, but to show the adaptability of the previous copper model.

Experimental

Reagents and Solutions

Two ammoniacal nickel systems were investigated in the laboratory work: nickel-ammonia-sulfate (Ni-NH3-SO4) and nickel-ammonia-carbonate (Ni-NH3-CO3). The solutions were prepared with reagent-grade chemicals and de-ionized distilled water.

Two commonly used commercial extractants were used in this study, LIX 64N and P5100. To simulate industrial practice, the extractants were used as received without purification, although the diluted extractants were conditioned by preliminary loading and stripping as recommended by Ritcey. The extractants were diluted to nominal compositions of 1, 10, and 25 vol pct with either Kermac 470B or Solvesso 100. The effective concentration of the extractant in each solution was determined by saturating with copper by repeated contact with excess copper ammonium sulfate solution at pH = 7.5. This saturation loading was used to calculate the molar concentration of the extractant.

Tests and Procedures

The tests were divided into shakeout and loading curve series. A shakeout test consisted of placing 50 mL each of a specific aqueous phase and a specific organic phase in a separatory funnel, shaking for 30 min in a thermostated shaker at 25° or 40° C, allowing the phases to settle and finally separating them. Preliminary tests indicated that 30 min was much longer than necessary to reach equilibrium. A shakeout series includes all the shakeout tests involving the range of aqueous-phase compositions extracted with a specific composition of extractant. A loading curve series is a limited shakeout series using a particular ionic strength and achieving a specific value of pH in the final (equilibrium) aqueous phase.

The aqueous feed concentrations used are shown in table 1. Nickel concentrations were chosen to cover the range from 25 to 120 pct of the stoichiometric capacity of the solvent being contacted. The desired ionic strength was obtained by adjusting the concentration of ammonium sulfate or ammonium carbonate. The pH of the feed liquor was adjusted by addition of ammonia at the beginning of each test.

After completion of the shakeout tests, the feed liquors and raffmates were analyzed for pH, Ni, SO4, or CO2T, (the total of CO2-containing species including CO2, CO3²-, HCO3-, NH2COO, etc.), NH4T (the total of all NH3- containing species including NH3, NH4+, i Ni(NH3)i²+, etc.), and in the sulfate system for NH3, (complexed) and NH3 (total). Nickel was determined by titration with ethylenediaminetetraacetic acid (EDTA) or induction coupled plasma spectrometry. Sulfate was measured gravimetrically as the BaSO4 precipitate. The CO2T was measured with a Leco carbon-sulfur analyzer, where the aqueous samples were ignited and the CO2 measured by infrared absorption. The NH4T was determined by a modified Kjeldahl method. In the sulfate system, the NH3 (total) was analyzed by acid titration, and the NH3 (complexed) (the sum of the NH3 in the Ni(NH3)x²+ complexes) was calculated by estimating the mean coordination number by absorption spectrophotometry and multiplying by the nickel concentration.

The final organic phases were analyzed for Ni and NH3. The nickel concentration in the organic phase was determined by wet ashing the organic sample and analyzing the resultant aqueous solution as above. The NH3 in the organic phases was determined by stripping with sulfuric acid solution and analyzing for NH4+, as above.

In the shakeout series designed to measure the effects of initial pH at various conditions, nickel concentrations corresponded to 25, 50, 75, 100, and 120 pct of the stoichiometric extractant concentration. The pH of the feed liquor was set at 7.5, 8.5, or 9.5 in the sulfate tests and 8.0, 9.0, or 10.0 in the carbonate tests. The ammonium sulfate or ammonium carbonate concentration was nominally 1M or 2M, while the nominal extractant concentration was 1, 10, or 25 vol pct.

The loading curve series, designed to measure nickel extraction at a given equilibrium raffinate pH, are more useful from a theoretical point of view, but are not as directly applicable to the usual industrial situation. These tests were also more difficult to conduct because the initial pH had to be adjusted to produce the desired raffinate pH, and this adjustment was often more difficult than expected. Therefore, only a few loading curve series were run, and these were generally near the mid-range of the conditions studied.

Precision

The major experimental series were run in triplicate to estimate experimental reproducibility. The estimated relative standard deviation for experimental replication was about 2 pct for SO4²-, 7 pct for Ni extraction, and 14 pct for NH3 extraction. The repeatability of raffinate pH was about ±0.05 pH unit. The accuracy of the pH measurements was estimated to average ±0.02 pH unit.

Mathematical Basis for Model

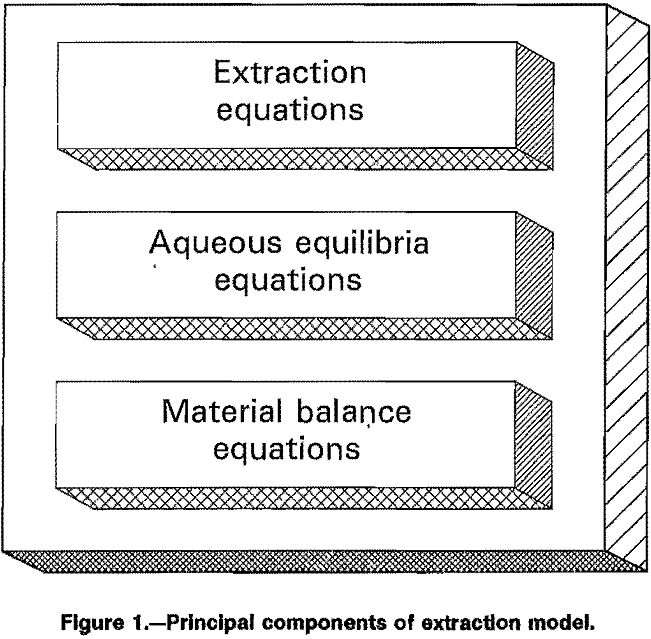
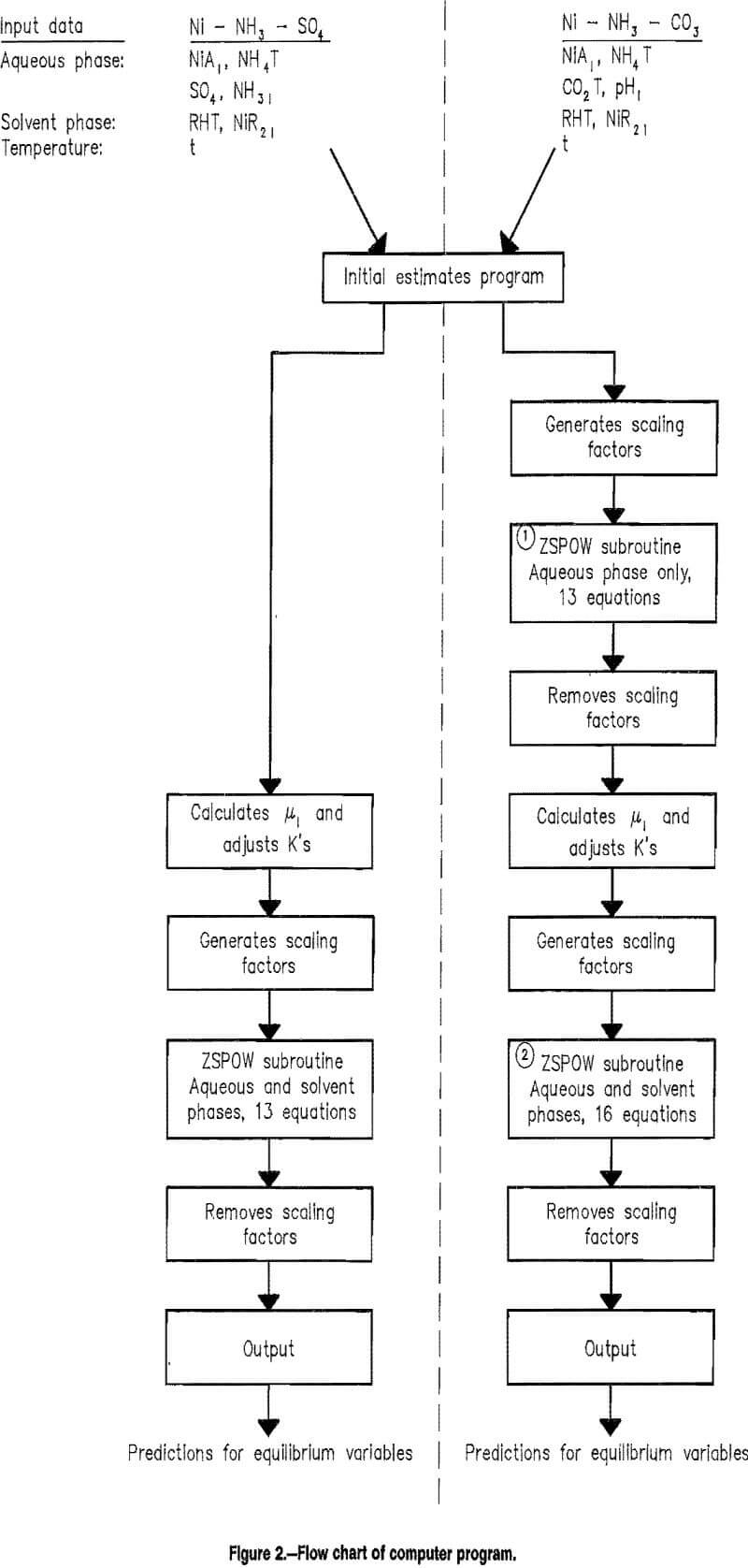
The mathematical model uses the known starting conditions (nickel concentration, ammonium salt concentration, pH, extractant concentration, etc.) to calculate the final compositions after extraction. Thus, the extraction model includes equations describing the extraction equilibria, the various equilibria in the aqueous phase, and the appropriate material balance equations (fig. 1).

Extraction Equations

A major objective of this research was to develop a mathematical equation describing the equilibrium relationship for extraction of nickel from ammoniacal solutions over a broad range of conditions. Extraction of ammonia must also be considered in such systems. Either of the two general classes of equations could be used to meet the

objective: mechanistic or empirical. Each class has its advantages and disadvantages, and both procedures were attempted in this research.

The mechanistic approach assumes a set of reaction equations which is thought to describe the actual reaction mechanism. If the correct reactions are selected, then the set of mechanistic equations should describe the extraction over the full range of possible conditions. However, the complete and correct reaction set is not known. The procedure then becomes largely a matter of intuition about the chemistry of the extraction applied to trial-and-error.

The extraction of divalent cations from ammoniacal solutions by hydroxyoximes has often been represented simply by the reaction equation;

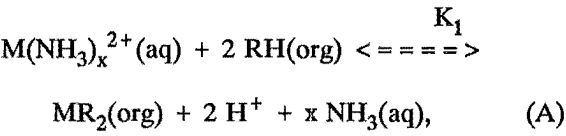
where M = divalent metal, nickel in this case,
RH = extractant in the solvent phase,
x = average coordination number of the metal ion,
and K1 = equilibrium constant for the reaction.

However, a better approach would be to assume the reactions

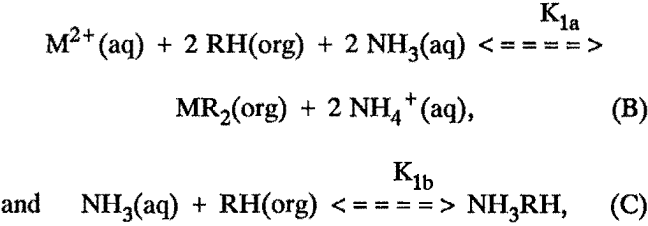
and include the aqueous equilibria equations discussed later. In general, the equilibrium constants in these equations cannot be determined analytically, and iterative methods must be used. These equations ignore some of the details of the chemistry involved, such as the possible polymerization of the extractant, possible complexation of the extracted molecule by additional extractant, etc. Unfortunately, inclusion of these possibilities increases the mathematical difficulty considerably, and preliminary efforts did not show a significant improvement of the fit to the data.

Empirical extraction equations ignore the actual reaction mechanism, and simply use a form and parameters that fit the experimental data. Usually, the form of the equation selected is one that is mathematically tractable. The advantage of the empirical equations is that useful results can be obtained relatively easily. The disadvantages are that the equations reveal nothing of the reaction mechanisms and are usually applicable only to a limited range of conditions.

The empirical equations used were fairly simple logarithmic equations of the form:

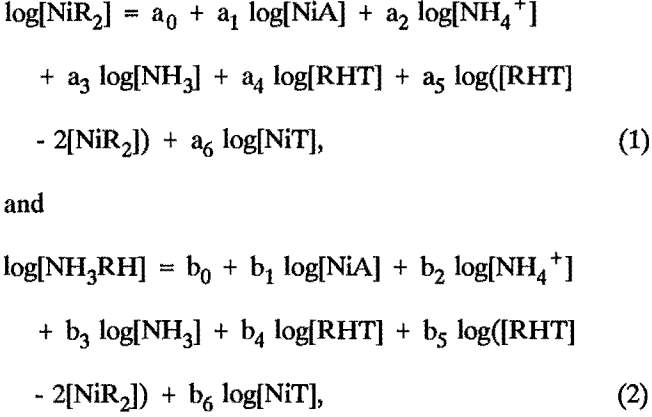
where [NiR2] = the concentration of extracted Ni,
[NH3RH] = the concentration of extracted NH3,
[NiA] = the concentration of Ni in the final aqueous phase,
[NiT] = the total of the concentrations of Ni in the test,
[NH4+] = the concentration of the NH4+ ion in the final aqueous phase,
[NH3] = the concentration of the aqueous NH3 in the final aqueous phase,
[RHT] = the total equivalent concentration of all the extractant-containing species in the test;

and a0, a1 and b0, b1 are coefficients that depend on the extractant, diluent, and temperature used.

The coefficients were determined by using stepwise multilinear regression to find the best fit to the experimentally measured equilibrium concentrations. Only those coefficients that had less than a 5-pct probability of being zero were included in the final equations.

Aqueous Equilibria Equations

In addition to the equilibrium extraction expressions, the overall extraction model must include the aqueous equilibrium reactions and mass balance equations. The aqueous chemistry in the ammonium sulfate solutions must include the following equilibria:

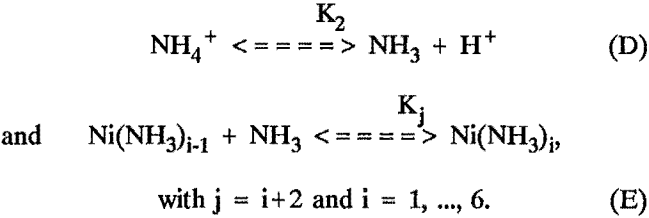
When modeling extraction from ammonium carbonate solutions, the following additional equilibria were considered:

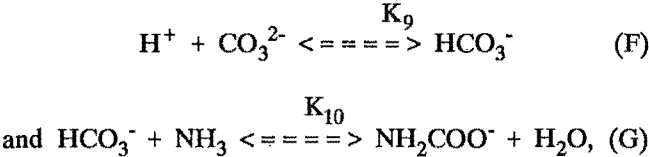
but carbonate-containing complexes and free carbon di-oxide were neglected.

Equilibrium Constants and Expressions

Numerical equilibrium constants or expressions are necessary to use the equilibrium equations. In most cases, literature values were adequate, but in some cases it was necessary to develop empirical expressions to describe the equilibria in the high-ionic-strength solutions of this investigation.

An empirical equation for the effective equilibrium constant for the dissociation of ammonium ion in ammonium sulfate solutions was reported in a previous report. This equation is

-log(K2) = 0.1774 + 2,727/T + 0.2985 (µ)½…………………………….(3)

where concentrations are expressed in moles per liter,

log = logarithm to base 10,
T = temperature, K,
and µ = the ionic strength.

In the ammonium carbonate system, the authors found that the carbonate-bicarbonate equilibrium constant can be estimated as

log(K9) = 7.68 + 652/T……………………………………………………………….(4)

An equation was obtained from the literature for the equilibrium constant for carbamate formation at various temperatures:

log(K10) = -3.7 + 1,260/T…………………………………………………………(5)

Literature values were used for the nickel-ammine complex instability constants:

log(K3) = 2.72 + adj…………………………………………………(6)

log(K4) = 2.17 + adj………………………………………………….(7)

log(K5) = 1.66 + adj…………………………………………………(8)

log(K6) = 1.12 + adj…………………………………………………(9)

log(K7) = 0.67 + adj……………………………………………….(10)

and log(K8) = -0.03 + adj………………………………………..(11)

where adj is a uniform adjustment for temperature and ionic strength,

adj = 0.054 µI – 860 (1/298 – 1/T)…………………………………………..(12)

The mean coordination numbers calculated from these constants and their equilibrium equations compared well with experimental coordination numbers determined from the wavelength of the spectrophotometric absorption peak.

Material Balance Equations

The extraction equations were developed from measured equilibrium concentrations, but in most applications only the starting conditions would be known. Therefore, supplemental mass-balance equations are used to provide the connection of starting conditions to equilibrium conditions.

The supplemental equations for the Ni-NH3-SO4 systems included the following equations:

Nickel balance:

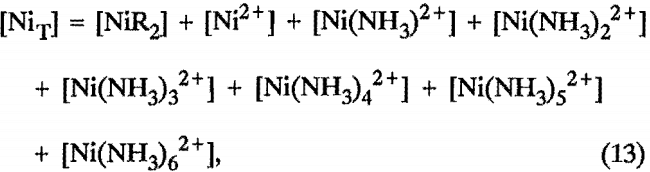
where [NiT] represents the total nickel in the system, including the nickel concentration in the feed liquor and any residual nickel in the extractant solution.

Total ammonia balance:

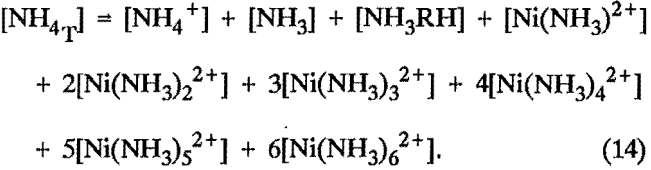
Extractant balance:

[RHT] = [RH] + 2[NiR2] + [NH3RH]………………………………………………(15)

Ionic balance:

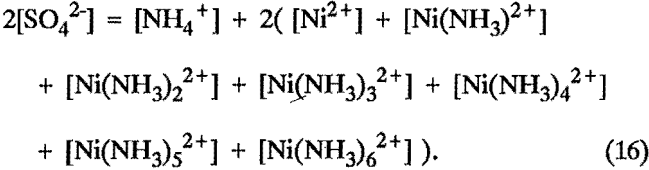
The [OH-] and [H+] ions were neglected because of their low concentrations.

In the carbonate system, some modifications to the balances of the sulfate system were necessary.

Total carbon dioxide balance:

[CO2T] = [CO3²-| + [HCO3-] + [NH2COO-]………………………………………….(17)

Ionic balance must be changed by replacing 2[SO4²-] with the sum:

2[CO3²-] + [HCO3-] + [NH2COO-]………………………………………………………….(18)

Computer Program

The application of all these mathematical relationships, which constitute the extraction model, to calculate the equilibrium concentrations from starting conditions involves the solution of a set of simultaneous nonlinear equations. An overview of the computer program is shown in the flow charts of figure 2. The procedure followed in this research was a FORTRAN program calling the IMSL subroutine ZSPOW, which uses a modified Newton procedure to iteratively solve the set of equations. Such iterative solutions require initial estimates of the variables, so the first part of the program used simplifying assumptions to obtain first estimates of the concentrations. To give each of the equations equal weight and put the variables in a range for best solutions, the variables were coded by mathematical transformations. Then the set of equations was solved, the variables were decoded, and the results were reported. One characteristic of an iterative solution to a problem is that a solution is not always obtained; sometimes the result oscillates or diverges. The subroutine tests for convergence, and if the result does not converge in 100 iterations, then the set of equations is considered not to have a solution. Also different solutions are sometimes found when different initial estimates are used.

A printout of the program is available from the authors on request.

Results and Discussion

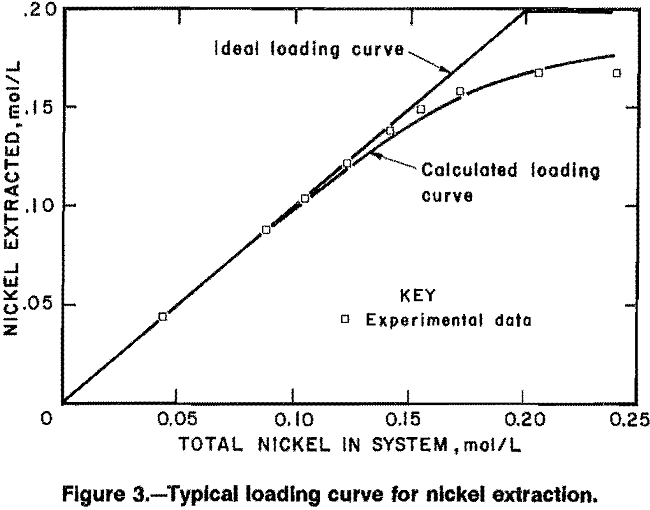
Typical loading-test data are shown in figure 3, along with the ideal-loading curve and the calculated loading curve. These data were obtained at approximately constant conditions of [NH4+] = 2.5 mol/L, [NH3] = 0.4 mol/L, and pH = 8.5, with increasing values of total nickel in the system, [NiT], The ideal-loading curve represents the case where essentially all of the nickel in the system is extracted by the solvent until the stoichiometric capacity is reached, and above that point the amount of nickel extracted remains constant. The calculated loading curve was obtained by using a simplified form of the equilibrium equation that represents reaction B at constant conditions,

[NiR2] = Kap [NiA] [RH]2……………………………………………………….(19)

with the apparent equilibrium constant, Kap = 1,250. The average error in this case is less than 3 pct. A small set of data, such as this loading curve, usually can be fit by an equilibrium equation, but a more general relationship, to fit data obtained over a broad range of conditions, requires consideration of all the reactions in the aqueous and organic phases.

Several mechanistic extraction equations were developed for extraction with LIX 64N in Kermac 470B at 40° C. The sets of equilibrium constants that fit best, and the resultant average errors, are shown in table 2. The average error of about 27 pct is larger than expected, but the simplest set of equations was tested in the full model anyway. However, mechanistic equations to fit the data obtained under other conditions gave worse results.

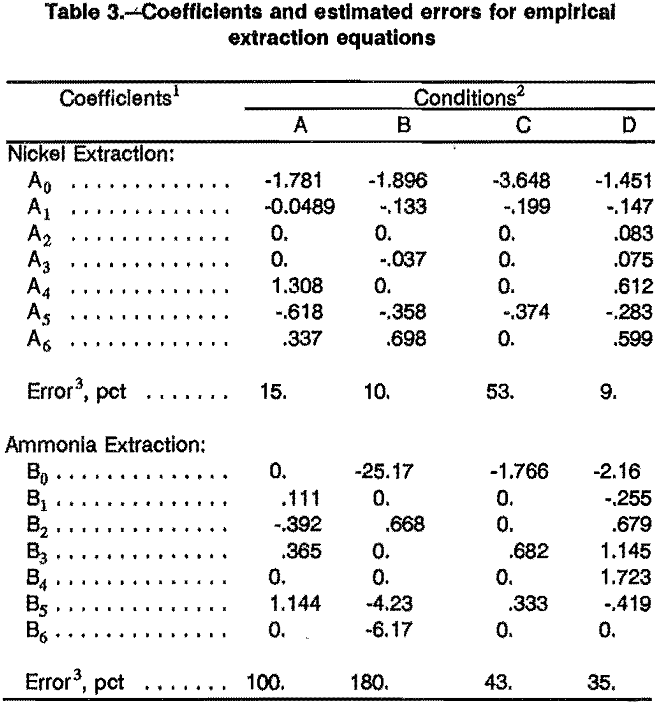
Empirical equilibrium equations were obtained for all conditions used. The coefficients and average errors are shown in table 3. The estimated nickel extraction errors for the tests using Kermac 470B solvent were 15 pct or less, and will be used in the full model. The estimated error for the tests using Solvesso 100 was around 50 pct, and a full model was not developed for these conditions.

Using the extraction equations discussed above, models were developed for the extraction of nickel from the two principal ammoniacal systems that have been used in the hydrometallurgical processing of ores, ammonium sulfate and ammonium carbonate. When the mechanistic-based equilibrium equations were used to model the extraction with LIX 64N in Kermac 470B at 40° C, the model tended to give poor results and often did not converge. Also, the empirical equation in the model of the 25° C data was not successful because of poor convergence.

Because of the difficulties encountered at the other conditions, the results presented here correspond only to the extraction of nickel at 40° C with solvents containing LIX 64N or P5100, each in Kermac 470B. The computer models used the appropriate empirical equilibrium equations. Table 4 shows the results of applying the model to a specific extraction test. Comparison of the predicted concentrations with the actual measured concentrations shows that in this case the prediction was fairly good.

The application of the model using initial conditions from all of the tests is summarized in table 5. The data only apply to ammoniacal conditions, so the few cases in which the pH dropped below 7.0 were not included in this summary. The average error for nickel extraction at the various conditions ranged from 5 to 27 pct, while that for ammonia extraction ranged from 40 to 100 pct. The unusually good fit of the model to the carbonate data using LIX 64N, average error of 5 pct, may be fortuitous.

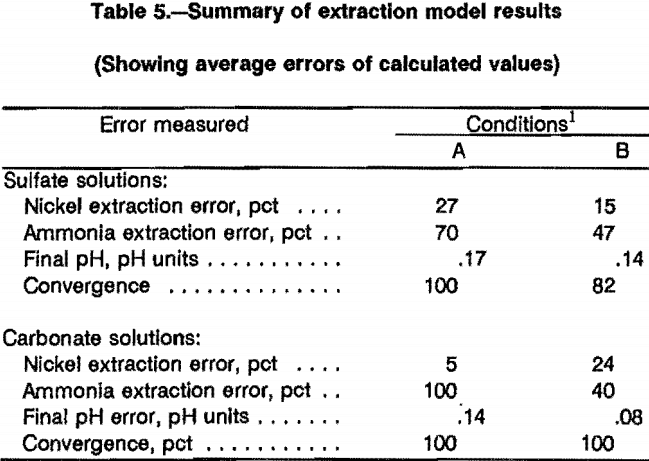
The results of the computer modeling are shown in figures 4 and 5, where the predicted nickel extraction is plotted against the experimentally measured extraction. Perfect prediction would lie along the diagonal line. Figure 4 shows the results for extraction with LIX 64N, with 4A showing extraction from ammonium sulfate solutions and 4B from ammonium carbonate solutions. In figure 4A, the data are generally grouped around the diagonal line, with a fairly large scatter; two points predict substantially less extraction than was measured. In 4B, the data are grouped even more closely to the diagonal line.

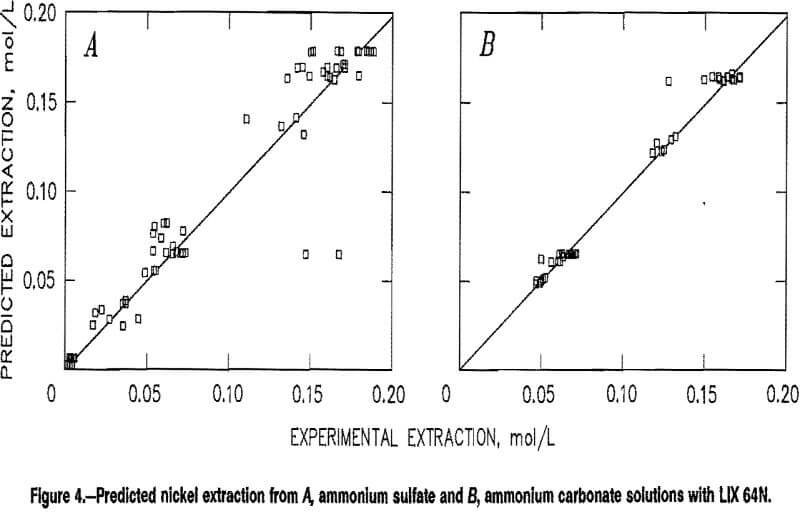
Figure 5 shows the results of applying the computer model for extraction with P5100; again 5A is for extraction from ammonium sulfate solutions and 5B from ammonium carbonate solutions. In both cases about half the data are grouped closely to the diagonal line, and the remainder of the data seem to show a systematic trend to predict lower than actual extraction. This appears to be a systematic deviation, but might indicate the effects of the initial estimates subprogram used.

Conclusions

Solvent extraction experiments were conducted over a wide range of conditions, extracting nickel from ammonium sulfate and ammonium carbonate solutions. A computer model was developed that was successful in predicting nickel extraction to within about 15 pct under certain conditions. Most of the experiments used LIX 64N extractant dissolved in Kermac 470B at 40° C. The initial nickel concentration ranged from 0.003 to 0.24 mol/L; the total concentration of all the ammonium species ranged from about 0.2 to 7.2 mol/L; and the pH ranged from 7.5 to 10. Additional tests were made, generally over a smaller range of concentrations: some at 25° C, some using Solvesso 100 diluent, and some using P5100 extractant.

Sets of mathematical equations were developed to describe the nickel extraction and ammonia extraction at the final equilibrium. A set of equations based on the assumed chemical reactions was moderately successful in describing the equilibrium relationships of the primary data set, but was not successful for the data at the other conditions. Empirical equations were found that better described the equilibrium relationships for all the data sets, except that using the Solvesso diluent.

Models incorporating the equilibrium equations with aqueous equilibria and material balance equations were used to predict equilibrium conditions from initial conditions for the experiments using LIX 64N or P5100 in Kermac 470B at 40° C. Models developed for the other conditions failed to converge for a majority of the tests. Perhaps the failure to converge, and even some of the poor predictions in those cases that did converge, are the result of the initial estimates used. Unfortunately, better methods of making the initial estimates have not yet been found.

At least two areas of potential future research are indicated: (1) Find methods to improve the convergence for the extended conditions (at 25° C, or using the more aromatic solvent), probably by improving the initial estimates. (2) Identify more completely the reaction species so that mechanistic equilibrium equations can replace the empirical equations.