The laws of comminution of Kick and Rittinger have been debated for many years. Certain data obtained from ball mill and drop tests are found to be in approximate agreement with Rittinger’s law while other data would seem to support Kick’s law. In all these tests the energy required to produce a wide variety of particle sizes has been studied. Surface area has also been measured with considerable difficulty, at first because it was thought that the energy associated with crushing was that required to create new surface, later because of precedent and because a more fundamental variable was unknown.

Because of its industrial importance, comminution has commanded considerable technical attention and has been the subject of continuous study for nearly a century. A number of empirical rules have been proposed to make it possible for grinding energies to be predicted. Of these so-called laws of comminution those bearing the names of Kick and Rittinger have been most widely applied and debated.

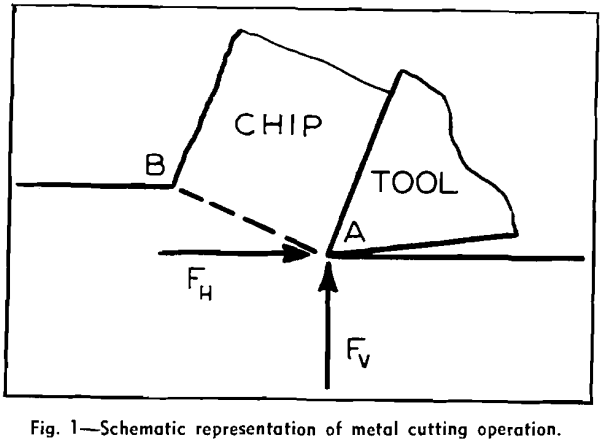
Kick’s law is based upon a critical strain energy concept. It states that the energy required to fracture a specimen is directly proportional to its volume and independent of the number or size of particles into which it is reduced. Stated algebraically this is

U = K1 V…………………………………………………………………………[1]

where U is the energy to which the volume V must be subjected to cause fracture and K, is a proportionality constant.

U = K2 (A2 – A1)……………………………………………………………[2]

where U is the energy required to crush a material when the change in area involved is (A2 – A1), and K2 is a proportionality constant.

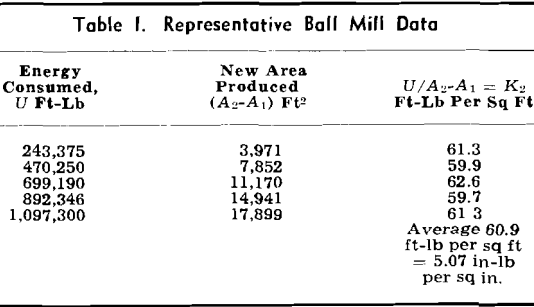
Investigators using Rittinger’s law have found that crushing efficiencies are generally extremely low. Some data of Martin who crushed quartz in an 18 x 18-in. tube ball mill using 1-in. diam balls are shown in Table I.

In addition to comminution there is a second grinding process practiced on a wide industrial scale. This is the type of grinding done in the machine shop, where the objective is to produce a smooth, dimensionally accurate surface. Unlike the powders produced in comminution, the small chips formed in machine grinding are not of value and hence are usually discarded. Even though the objectives in comminution and machine grinding are diametrically opposed, there is considerable similarity between the two processes.

 

 

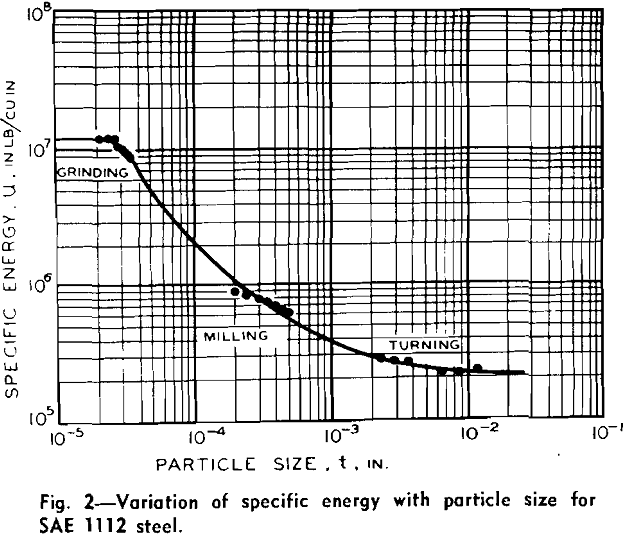
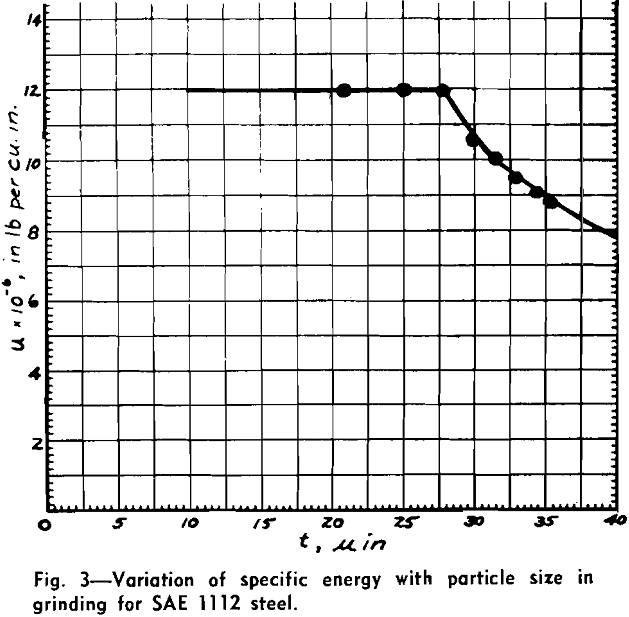
The calculation of the energy consumed per unit volume of metal cut or specific energy is one of the parameters which has proved to be very important in metal cutting studies. When the depth of cut, t, taken by a tool, is decreased, the specific energy, u, is found to increase.

When an energy balance is made for a cutting operation it is found that practically all the energy is associated with the shear and friction processes. As in comminution, the surface energy involved in the generation of new surface is negligible, and energy associated with change in velocity of the metal as it crosses the shear plane also can be neglected.

u = us + uf………………………………………………………………………[3]

where u is the total energy per unit volume of metal cut, u, is the shear energy per unit volume, and u, the energy per unit volume required to overcome friction on the tool face. Since in plastic flow the shear energy per unit volume (us) is equal to the product of the average shear stress and the shear strain, then

u ≅ 2 us ≅ 2τγ………………………………………………………………….[4]

Since γ is approximately 3

τ ≅ u/6…………………………………………………………………………….[5]

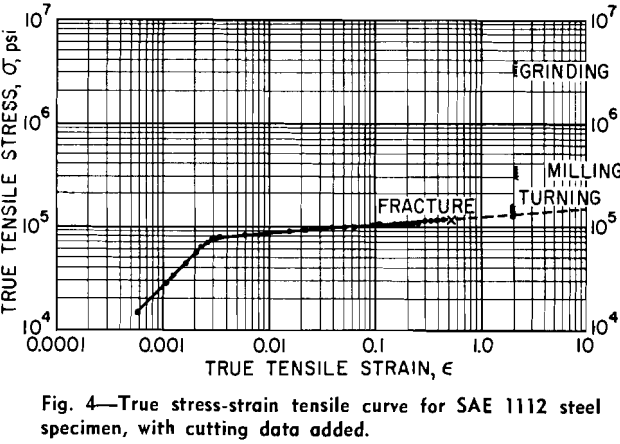
For a long time physicists have held that metals should exhibit much higher values of flow stress and strength than they actually do. The strength of a metal specimen is found to be G/2π, where G is the elastic shear modulus of the metal, in one approximate calculation based upon the forces required to slide one layer of atoms over another in a material having a perfect lattice structure. For steel, G is about 11.5×10 6 psi, and hence the theoretical shear strength of a steel specimen with no lattice imperfections should be about 1.8×10 6 psi, i.e., 11.5×10 6/2π. This value is seen to be in good agreement with the 2×10 6 psi observed for the maximum shear stress in fine grinding. I

The laws of Kick and Rittinger will now be interpreted in terms of the metal-cutting data that have been presented. If both sides of Eq. 1 are divided by the volume of the particle, then

u = U/V = K1………………………………………………………………………[6]

which states that the energy per unit volume is a constant.

V1 = V2 = V…………………………………………………………….[7]

If both sides of Eq. 2 are then divided by V,

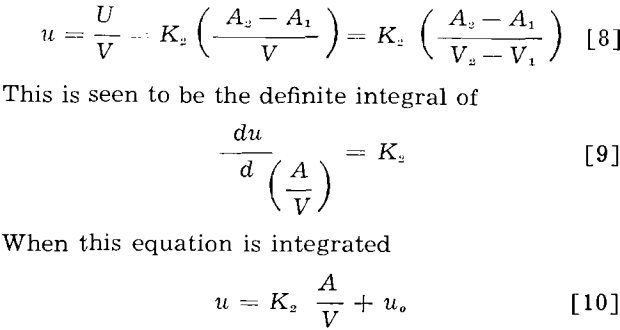
is obtained where uo is the integration constant. However, as indicated in Eq. 11,

A/V = l/t………………………………………………………………….[11]

V varies directly with the product of A and t where t is a mean thickness of the layer removed. Hence, from Eq. 10 and 11

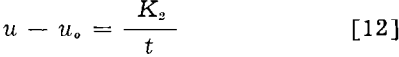
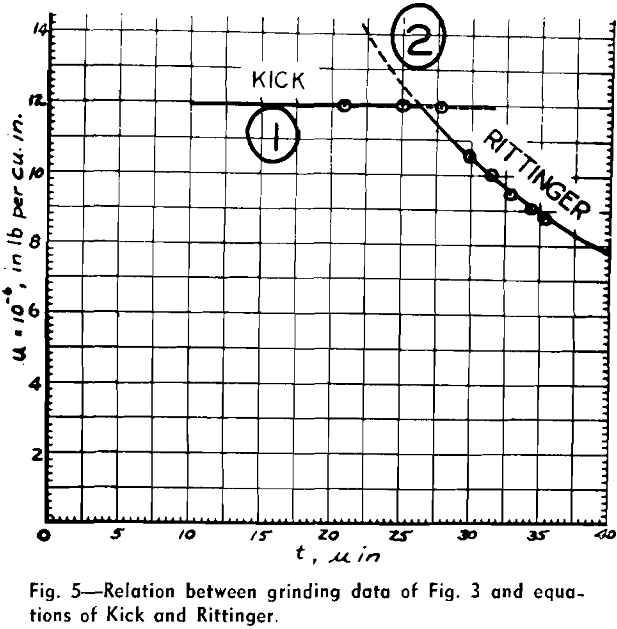
In Fig. 5 the data of Fig. 3 are shown replotted, and curve 2 is drawn in accordance with Eq. 11, the constants being:

uo = 200,000 in.-lb per cu in.
K2 = 300 in.-lb per sq in.

This curve is seen to be in good agreement with the grinding data. However, when this same curve, 2, is plotted with all the cutting data, see Fig. 6, the agreement is not quite as good. The milling data would appear to be in better agreement with curve 3 having constants

uo = 416,000 in.-lb per cu in.
K2 = 103 in.-lb per sq in.

From this comparison of the laws of Kick and

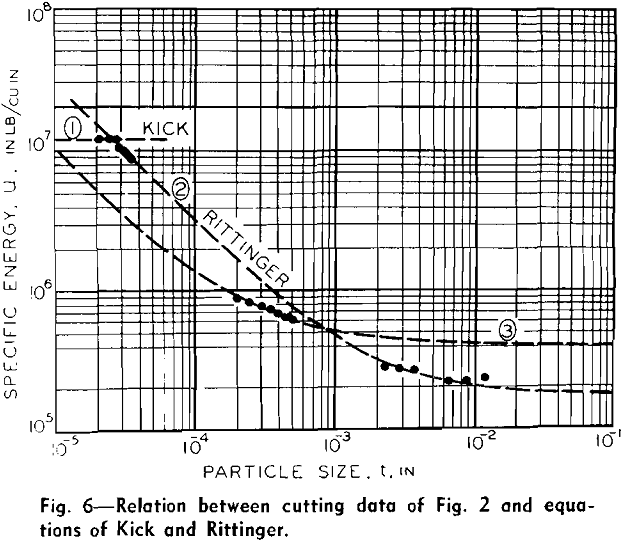
Rittinger with metal cutting data it is evident that Kick’s expression

U = 11.95 V in.-lb……………………………………………..[13]

is in good agreement with cutting data when the depth of cut is less than about ¾ micron, while Rittinger’s expression

U = 300 ΔA in.-lb……………………………………………..[14]

is in good agreement with the grinding data, while the expression

U = 103 ΔA…………………………………………………….[15]

 

u – 200,000 = 300/t in.-lb. per cu in………………………………………….[16]

Mineral Grinding

To investigate any differences that might be observed between the machine grinding of ductile metals and materials normally considered brittle, tests similar to those already described for metals were performed on minerals. The detailed test procedure is to be found in reference. Some grinding tests were run using a 46-grit 8-structure aluminum oxide wheel, while others were made using a 24-grit aluminum oxide abrasive belt. The belt made it possible to remove chips of greater size than could be handled by the wheel.

tinger’s law holds quite well over a limited range of size it must only be regarded as a first approximation when it is applied over a wider range.

Plastic flow in grinding or any type of cutting process can be carried to far greater strains without rupture than in the case of a tensile specimen. For example, the strain to rupture in a true-stress-strain tensile test is about 0.5, while the corresponding strain in cutting the same material will be 2.0 or more without rupture. The reason for these large strains lies in the fact that a large normal stress is present on the shear plane in cutting, and this normal stress increases the rupture stress.