Basic Principles: In a batch mill the length of time during which the material is ground is a direct measure of the energy expended on the material, except possibly for exceedingly fine grinding. The following analysis pertains to a continuous mill operating under these conditions.
dE = -C dx/x n…………………………………………..(1)
where dE is an infinitesimal energy expenditure, C a constant, dx an infinitesimal size change, x the particle size, and n a constant. F
(dtr)P = -C’ dx/x”………………………………………………………..(1a)
where dtr is an infinitesimal time during which a particle of size x is in the mill, and C’ is a constant.
A ground product never consists of particles of single size but always comprises a distribution of sizes. In comminution, the expenditure of energy causes a lateral shift in the size distribution.
y = 100 (x/k)a………………………………………………(2)
or in differential form:
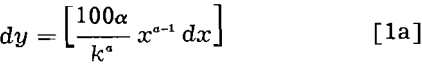
where y is percentage of material finer than size x, α is a constant that determines weight distribution among particles of various sizes, and k the size modulus that denotes the theoretically maximum-sized particle in any size distribution.
By considering the energy required to reduce an element of weight of material, dy, from size xm, to size x, the element of time during which the material must remain in the mill at constant power will be
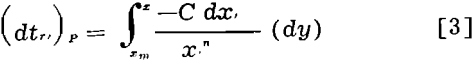
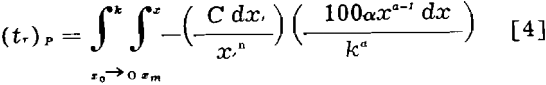
where xo, the size of material when y is zero, approaches zero. Thus for reducing material of large initial size to a product conforming to the Schuhmann size distribution of size modulus, k, the retention time within a continuously operating mill is given by
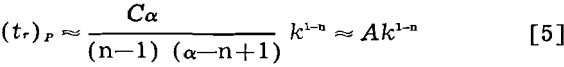
If an ore is ground in the vibratory ball mill under conditions where the retention time varies, a log-log plot of the size modulus, k, vs the retention time at constant power, (tr)P, should yield a straight line of slope 1-n.
Where the feed and product size distributions have identical values of α, and where the feed term is not negligible, the general equation will have the following form:
![]()
where kp and kf are the size moduli of the product and feed, respectively.
Materials and Method: A 15×15-in. Allis-Chalmers vibratory ball mill was operated in continuous open circuit to dry grind chromite. This mill, which was charged with 332 lb of balls (3 pct 1 in. by 7/8 in., 60 pct 7/8 by ¾ in., 37 pct ¾ by 5/8 in.), required 5.60 ± 0.05 kw for operation at a frequency of 1260 rpm and a vibration radius of 9/32 in.
The procedure used in the experimentation was to pass about 1000 lb of ore through the mill at 1200 lb per hr. The product from the mill was passed through the mill again at 1200 lb per hr until five passes had been made. In each case, samples of the product were taken after 5, 10, 20, 30, and 40 min of operation. Size distributions of these samples were identical, which shows that steady state had been reached before 5 min had elapsed.
Experimental Results: These data show that the product from the first pass through the mill has attained the equilibrium value of a, namely, 0.80, and that the size distributions are shifted laterally with each subsequent pass through the mill. In each case the size distributions are parallel straight lines over an important part, and the size modulus is the extrapolated straight-line portion to y = 100.
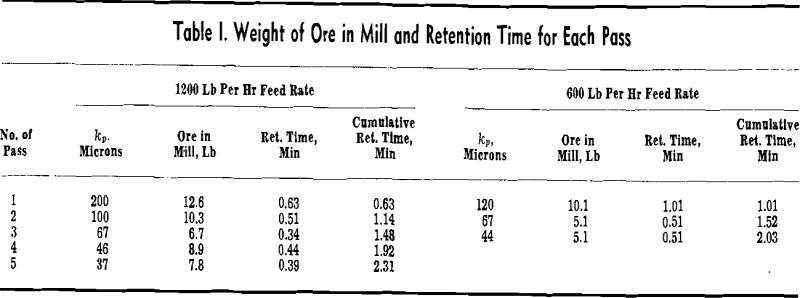
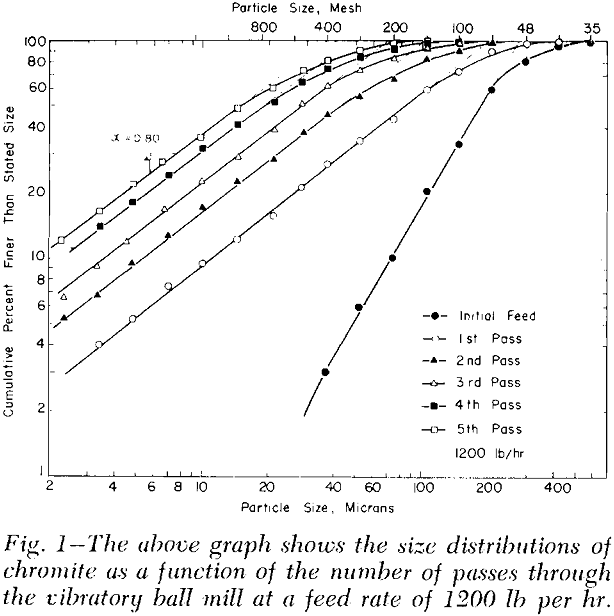
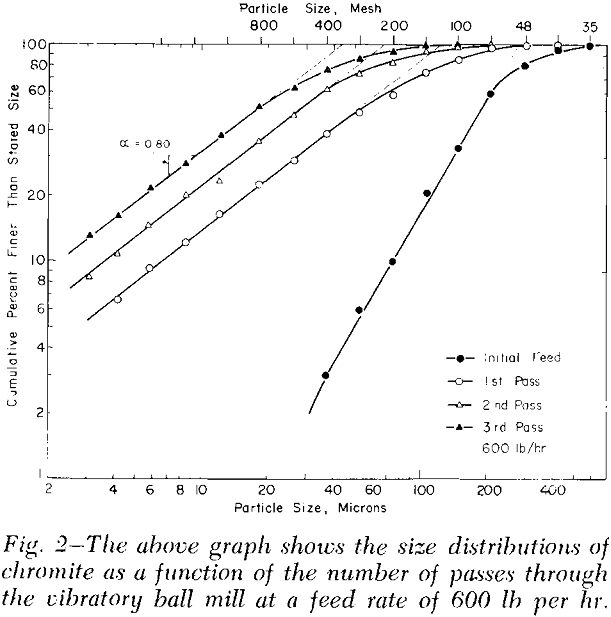
Since relatively coarse chromite was ground at constant power in the vibratory ball mill, n can be evaluated according to Eq. 5 by plotting on log-log paper the size modulus, k, vs the cumulative retention time, (Tr)p.
Discussion of Results: The experimental data reported in this paper show that for a vibratory ball mill operating continuously in open circuit, at constant power input, size moduli of the products are determined by total retention time within the mill, regardless of feed rate. Thus, for a continuously operating low-level discharge mill retention time determines how long any given particle is subjected to the mill action. In batch grinding the total grinding time is the retention time, and doubling the grinding time doubles the retention time. However, in continuous grinding the factors which determine retention time are complex in that retention time depends on flow characteristics of the material passing through the mill. For dry grinding in a vibratory mill, the scale-up of batch laboratory tests to continuous operation will be difficult without a knowledge of retention time, and this may entail experimental determination of retention time.

