Two particles in mutual contact form a system which is not in thermo-dynamical equilibrium, because its total surface free energy is not a minimum. If such a system is left for a certain period of time, the bonding of the two particles will take place in order to decrease the total surface area, even though the temperature is lower than the melting point. This phenomenon of bonding of two or more particles with the application of heat only and at temperatures below melting point of any component of the system will be called sintering, although the powder metallurgists use this term in a broader sense, including the presence of molten phase and pressure. It is the objective of this paper to study this process and the mechanisms involved in it.

J. Frenkel was the first to make a serious attempt to develop a theory of sintering. He assumed that the process consists of a slow deformation of crystalline particles under the influence of surface tension which reduces to a viscous flow where the coefficient of viscosity η is related to the self-diffusion coefficient D by the following equation

1/η = Dδ/kT……………………………………………………………….[1]

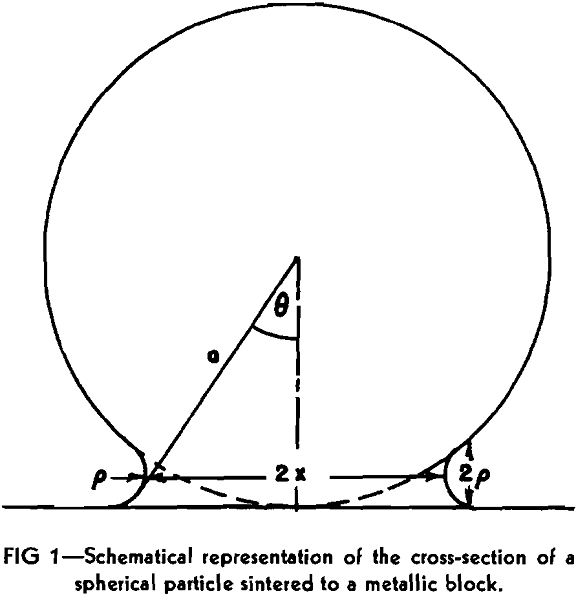
where δ is interatomic distance, k the Boltzman constant, and T the absolute temperature. This type of viscous flow of a crystalline substance is essentially different from the ordinary plastic flow. The latter is a specific property of crystals and cannot take place in amorphous bodies. According to Frenkel this viscous type of flow is due to the diffusion of the holes or vacancies arising in the lattice. He was able to derive an equation relating the growth of the interface between two spherical crystalline particles or between a particle and a semi-infinite crystal (Fig 1) to time t at constant temperature. This relationship can be written as follows:

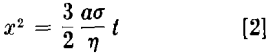
where x is the radius of the interface assumed to be circular, a the original radius of the sphere and σ surface tension of the material. The other assumptions are that x/a is less than 0.3 and that during the period t the original radius, a, of the metallic particle did not change appreciably.

 

Evaporation and Condensation

According to the kinetic theory the rate G of evaporation of a gas from a surface above which the equilibrium pressure is p1 and the rate of condensation on a neighboring surface of pressure p2 is

G = K(p1 – p2)…………………………………………………………………….[3]

where K is a function of temperature only.

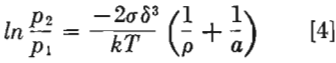
G = K’/P………………………………………………………………………….[5]

p = x²/2a

G = K”/x²

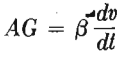
where β is independent of time.

In other words if the mechanism of evaporation and condensation were responsible for the formation of interface between particles, the radius of the junction should grow with such a rate that its cube would be proportional to time.

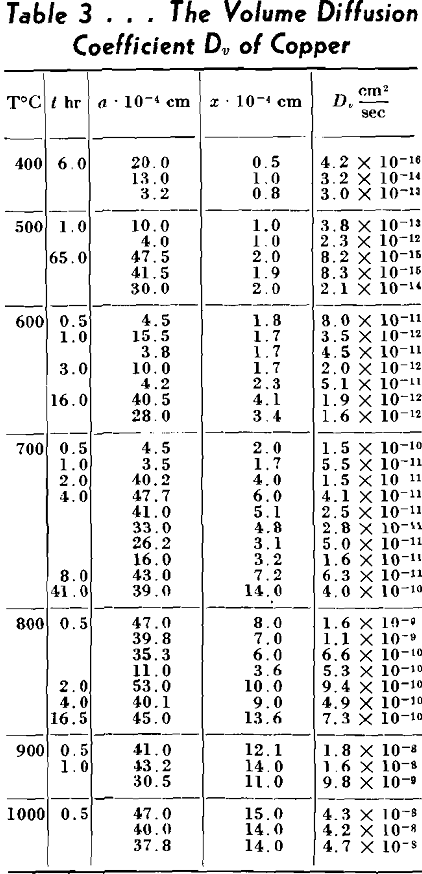
Volume Diffusion

If we assume the vacancy theory of diffusion, then the area near the

interface should have higher hole concentration than the remaining body of the particle. This is due to the fact that near the interface, where the radius of curvature is small the surface energy is very high and it can be lowered by decreasing the surface area. The decrease in surface area is produced by an increase in the interface volume which is accomplished by a larger concentration of vacancies present in that region. If the interstitial atom mechanism is assumed, the junction area should be deprived of the interstitial atoms in order to decrease the total surface. This causes the flow of atoms from the other parts of our system to the junction.

Experimental Method

In order to study experimentally the

 

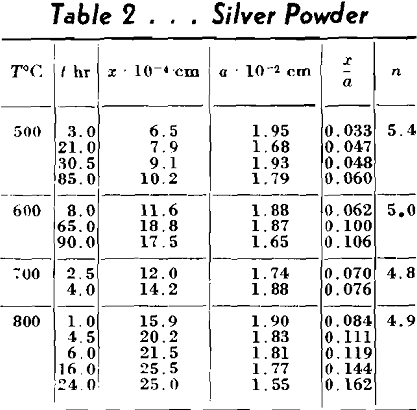
The metals used in these experiments were copper and silver. The copper was round, atomized powder obtained from Greenback Industries, Inc. The diameters of these particles ranged from 4 to 100µ. The powder was fractionated by the elutriation method into three lots. The first lot contained particles greater than 35µ in diameter. The second particles between 15-35µ and the third, particles less than 15µ. The silver used was coarse atomized powder of about 350µ, in diameter furnished by Stevens Institute of Technology. This powder consisted of almost perfectly spherical particles as can be ascertained from Fig 3, a and b. The copper powder contained some oxygen so it was reduced by packing it in carbon and heating in a hydrogen atmosphere at 900°C for 18-24 hr. The resulting powder developed some blow holes. The copper blocks were cast of oxygen free high conductivity copper, the silver was spectroscopically pure. Their surfaces were thoroughly polished and cleaned by etching before the powders were dispersed on them. The copper was etched with ammonium hydroxide plus hydrogen peroxide and the silver specimens with potassium dichromate. After heating, the specimens were plated with nickel in order to avoid loosening or deforming the interfaces during the subsequent metallographic operations.

As nobody has ever before measured the coefficient of surface self-diffusion, data obtained in this work cannot be checked but the order of magnitude appears to be reasonable. The fact that energies of activation of volume and surface diffusions are nearly equal may very well be explained by Schottky’s mechanism of diffusion. According to him all vacancies are generated on the surface, consequently the energy of the formation of vacancy should be the same in both cases.