Table of Contents
The adaptation of European methods of concentrating ores to suit the conditions of this country has followed the lines that simplify machinery, diminish labor and increase capacity. Noteworthy instances are the substitution of hydraulic classifiers for the last one or two trommels in the series, and the substitution of a distributing-tank for the slimes in the place of the Spitzkasten.
The question may be fairly asked, At what point do losses become serious in consequence of these changes? It is to study this question that the investigation herein described has been undertaken. After the losses are located and the methods of stopping them are pointed out, it will then lie with the individual mill to decide whether or not the plans proposed will save sufficient value to warrant their adoption.
In the discussion of sorting followed by sizing, as the terms are used in this paper, we have to deal with the preparation of slimes by the Spitzkasten for subsequent washing upon the slime-table.
The Spitzkasten, or pointed box, is an inverted hollow pyramid, generally of wood, usually with four faces or sides coming together in a point below. The sides can have, according to Rittinger, a minimum angle of slope of 50° with the horizontal. The feed-water carrying fine slimes (less than 0.01 inch, or 0.25 mm. in diameter) for treatment is fed at one end and carefully distributed over the whole width. The outlet is over the opposite end. The water-current passes direct from inlet to outlet, and has usually been regarded as a surface-layer passing over without much disturbing the stagnant layer of water below. Under such conditions the coarser grains of quartz, together with finer grains of the heavier metallic mineral—for example, galena—drop out of the current into the stagnant water below, and, settling to the apex, are discharged through a pipe or spigot. Several pointed boxes in series, each larger than its predecessor, will give a series of products, each of which is finer than its predecessor, and the particles will be approximately sorted according to the law of free-settling particles. This process of grouping together grains of metallic or specifically heavier mineral, which are smaller in size, with those of the non-metallic or specifically lighter mineral that are relatively larger in size, is called sorting the slimes, and the series of products are called slime-sorts.
A slime-table for washing ores has a true surface, either a plane or a much-flattened cone, with gentle slope, and upon the upper margin of it water is evenly distributed. The layer or film of water has an approximately even thickness if the table is plane, or a gradually decreasing thickness if the table is a convex cone, varied only by a series of slight waves, and is continuously moving down in the direction of steepest slope.
If, now, one of the above sorted products is placed upon such a slime-table, the particles of galena, for example, being small, settle upon the table and do not move, or move but slowly because they are in the lower slow-moving portion of the water-film, while the quartz-grains, being larger, reach up into the quick-moving water and are carried forward rapidly.
The operation of separating small grains from large grains is technically called sizing, whether it is done by putting the grains on a sieve of such a mesh that it allows the smaller grains to pass through while it holds back the larger grains, or, on the other hand, is done by a slime-table, which rolls the large grains rapidly towards its margin, but moves the small grains slowly or not at all.
By combining the two principles—namely, the Spitzkasten and the slime-table—we have what is called separation by sorting followed by sizing.
There is a dearth of exact data upon the laws defining the water-quantity and slope-angle best adapted for the treatment of the different slime-sorts upon slime-tables, and it is to supply this deficiency that the present investigation has been undertaken. The different writers give us figures derived empirically from mill-practice. Linkenbach gives for stationary slime-tables :
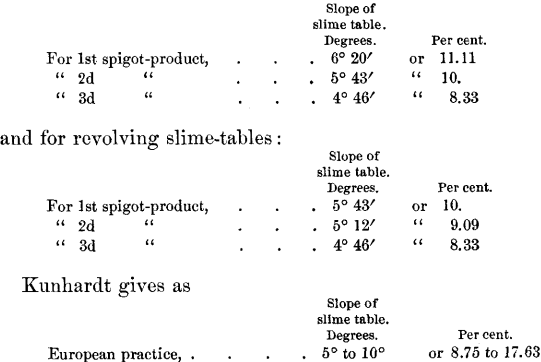
United States practice is illustrated by the list on the following page, comprising 25 slime-tables, in 20 mills, located in about 10 different districts. In this list a represents convex conical revolving tables ; b, convex stationary tables, and c, concave conical revolving tables.
To design machines of this class intelligently, we need to have exact data as to the angle at which :
- The quartz starts to roll.
- The quartz is all moving.
- The heavy mineral starts.
- The heavy mineral is all moving.
These observations should be taken with many different slime-sorts and quantities of water, ranging from very small to very large, to cover all possible demands.
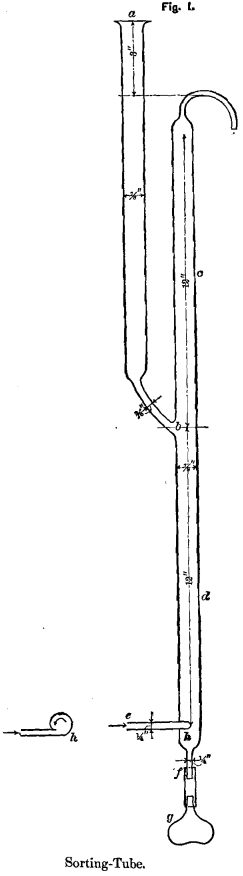
To obtain the desired experimental data, the author required at the outset a set of products as perfectly sorted as possible. For this purpose the sorting-tube, Fig. 1, was designed. Hydraulic water is fed at e at a constant rate, admitted by a dial-cock at constant pressure, guaranteed by an overflow column-pipe to give constant head. This passes up and overflows at i, at any desired speed. If k be the average area in square centimeters of the tube cd, then the grammes or cubic centimeters l of water delivered per minute at i, divided by k, will give the upward velocity m of the water in centimeters per minute :
m = l/k.
The same result may be obtained in inches per minute by weighing the water in pounds as follows: The pounds of water
at 62° F., p, delivered per minute at i, multiplied by 27.712, gives cubic inches, and this product divided by the area r in square inches gives the ascending velocity s in inches per minute :
s = 27.712 p/r.
The sorted products were obtained by feeding at a, in very small quantities at a time, mixed grains of quartz and galena, which had passed through a limiting-sieve of 10 meshes to the linear inch, and therefore contained grains of both minerals ranging from that size down to dust. The grains became subject to the action of the current at b. If they were light enough to rise in the current flowing at any given time they were discharged at i. If heavy enough to fall, they passed down to the bulb g. The rising portion c of the tube is 12 inches long, to give a heavy grain that distance to repent and return. The falling portion d of the tube is also 12 inches long, to give a light grain the same opportunity. A rotary motion is given to the water in d, to prevent a downward current on one side and an excess of upward current on the other. If the mixed quartz and galena is fed slowly, so that “ free-settling ” conditions prevail while the water is rising—for example, 40 millimeters per second—it yields two products: the overflow-grains which rise in a 40-mm. current, the bulb-grains which fall in the same current. If, now, we feed the above bulb-grains to the tube when the water is rising 50 mm. per second, it again yields two products: overflow-grains which rise in a 50-mm. current, and bulb-grains which fall in the same current. This second overflow is defined as consisting of grains of quartz and galena which, under free-settling conditions, fall in a 40-mm. current and rise in a 50-mm. current.
To obtain a complete set of products, as perfectly defined as the above, the water-current was rated at frequent intervals all the way from 0.0496 inches (1.261 mm.) per second to 7.8259 inches (198.777 mm.) per second. And to obtain further information, the length and width of each of ten grains of quartz and also of galena were measured by microscope-micrometer for each product. The average of the ten measures of length and of width (twenty in all) is called the average diameter of the grains. These figures are given in inches and in metric measures in Table I., together with the ratio of the average diameters of quartz and galena. The specific gravity of the quartz is 2.640 and that of the galena is 7.586.
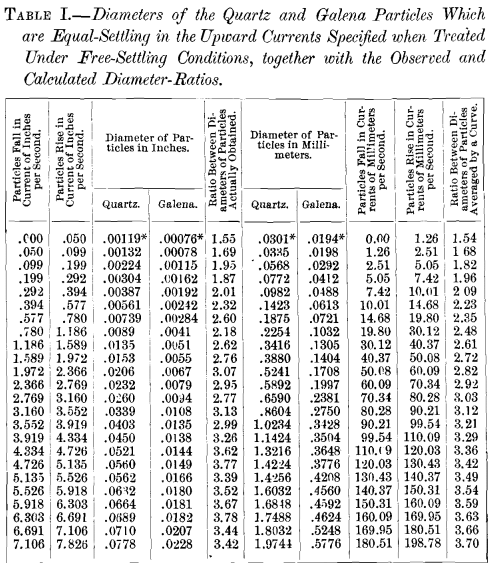
Before passing to the next step in our subject it is interesting to note that in the sorting by the sorting-tube, Fig. 1, the values here obtained for grains settling under free-settling conditions corroborate those given in “ Close Sizing Before Jigging,” showing again that for fine sizes the free-settling ratio of the diameter of the quartz particle to that of the galena particle is less than Rittinger’s formula would give, and that the ratio decreases as the diameters decrease (see Table I.). The measures of the diameters given in “ Close Sizing Before Jigging ” were made by sieves. The measures for this paper were made by micrometer in a microscope, and are therefore probably more accurate than those of the former.
The sorting apparatus having been obtained, and with it a very perfect set of sorted products, it was necessary next to prepare an accurate sizing-apparatus or slime-table. This is shown in elevation in Fig. 2 and in plan in Fig. 3.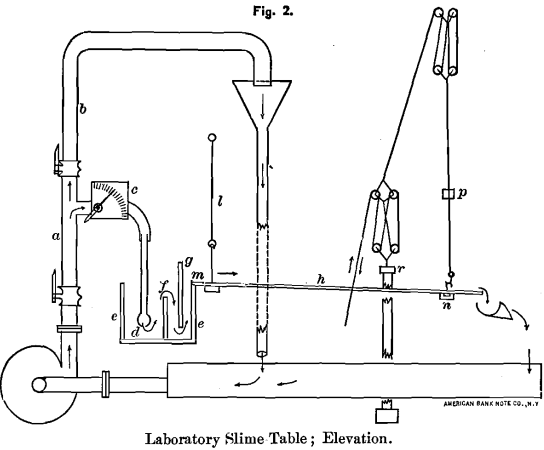
This apparatus (see Fig. 2) consists of a plane plate-glass h, with ground surface, capable of being fed with an even flow of water and of being tilted at any angle. The details are as follows:
a. A hydrant of 2-inch pipe supplied with water by a centrifugal pump.
b. A column-pipe, 8 feet high, to completely even up the pressure.
c. A dial-cock and hose for delivering constant quantities of water to the table.
d. A long rose-pipe delivering water the whole length of the distributing-tank e, which has a dam f, a baffle-plate or gate g, and an outlet over a straight edge, m.
h. A plate-glass ground surface, 2 feet wide, 4 feet long, suspended on two rods, l, at the head, and at the foot by a block and tackle, multiplying the movement 20 times by 4 double pulleys.
This table has a surface well adapted to its work. It appeared to be rough enough to cause the particle to roll, but not rough enough to obstruct its passage. It can be tilted at any angle from level to 45° slope and adjusted with minute accuracy. The angles were measured
by a Linton level, with a probable error of five minutes of arc; the film thickness on the crest and trough of the waves was measured by a micrometer gauge reading to 0.001 inch, with probable error in reading of 0.002 inch on wave-crests and 0.004 inch in the troughs, and where there was no wave, 0.002 inch. The sands to be treated were put on at 23 inches from the head and spread out in a straight line about 8 inches long at right angles to the direction of flow to prevent the grains from hindering each other. The quantity of water flowing was weighed in a bucket with a spring-balance weighing to sixty pounds, and reading to one-tenth of a pound, the limit of error being about 1 per cent.
An experiment is begun by gauging the water to a given number of pounds flowing off the tail. The charge of grains of quartz and galena is then put in place and the table is slowly tilted until
(1) the first grain of quartz starts.
Then, the angle of slope and the thickness of film on crest and trough are taken.
 The slope is increased gradually till each of the following events has occurred, stopping to take the above measures at each point :
The slope is increased gradually till each of the following events has occurred, stopping to take the above measures at each point :
(2) All the grains of quartz move.
(3) The first grain of galena moves.
(4) All the grains of galena move.
After these four sets of observations are concluded, the water is set at another rate of flow in pounds per minute and the whole series is recorded again. In this way the conditions are studied with small intervals, from a quantity of water which breaks down because it is too little at one end of the series, to a quantity which is absurdly large at the other end. The little end of the series for small grains was where the water failed to cover the table, for large grains, where events 2 and 4 occurred at nearly the same angle.
It will be observed that the method employed was to measure angles, films, etc., at the moment when a body at rest begins to move. If the opposite plan, namely, to measure angles, films, etc., when a moving body comes to rest, had been adopted, it would have represented more exactly what happens upon a convex conical slime-table. The difficulties of making the tests by the latter method caused the selection of the former. The difference in results is that the figures for angles given in the table are slightly larger than they would be if the coming-to- rest method had been employed.
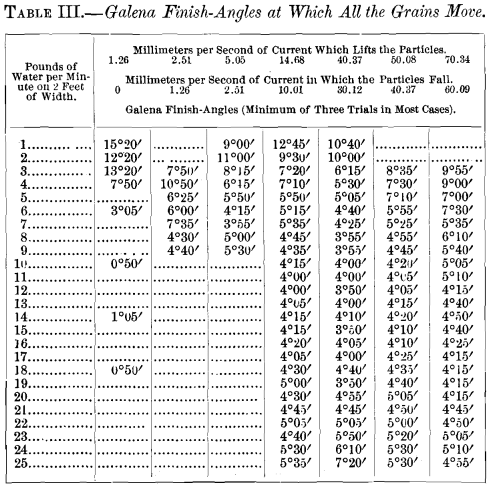
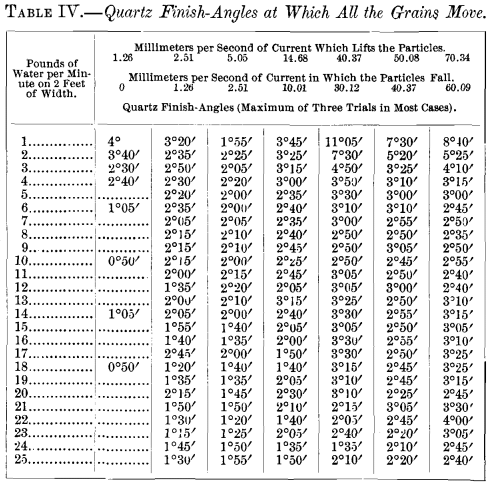
A portion of the measurements of angles obtained in this work are presented in Tables III. and IV.
Table III. gives the slope-angles at which all the particles of each of the different sorts of galena start to move. In most cases each figure is the lowest of three observations. They are called the finish-angles of galena.
Table IV. gives the slope-angles at which all the particles of each of the different sorts of quartz start to move. In most cases each figure is the highest of three observations. They are called the finish-angles of quartz.
This finish-angle of quartz is believed by the author to be the most important angle of all. From a table set at this angle nearly all the quartz will roll off, and nearly all the galena will remain on it at rest.
The starting-angles did not appear to the author to have the same value as the finish-angles in guiding the judgment for best slope and water for a given slime-sort, and have, therefore, been omitted.
In examining the starting-angles of galena and quartz it was noticed that the first grain of galena often starts at an angle smaller than the finish-angle of quartz. This is not as serious a matter as it appears, for several reasons. First, there were only a few light grains of galena that started before the quartz; secondly, they moved slowly, so that the quartz easily overtook and left them behind; and, thirdly, the occurrence was confined to those experiments that were near the least water-quantity, and therefore outside of the range of the best working conditions.
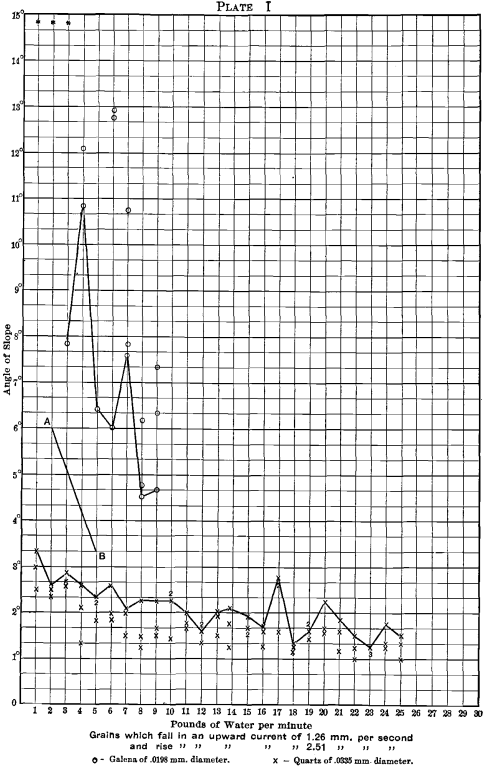
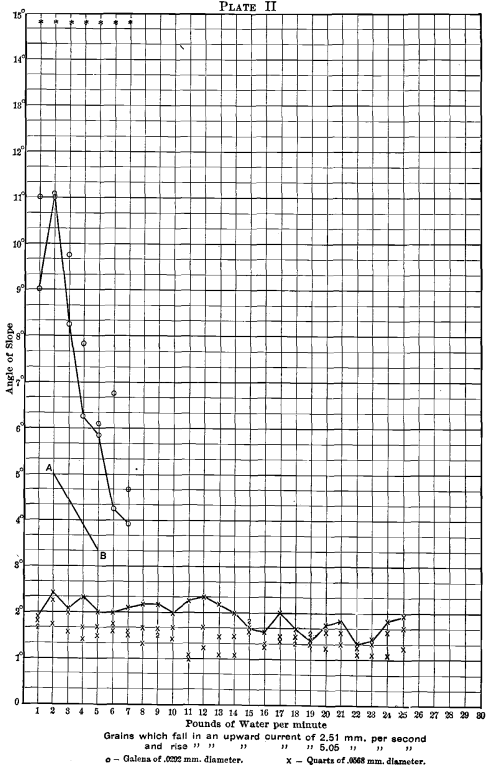
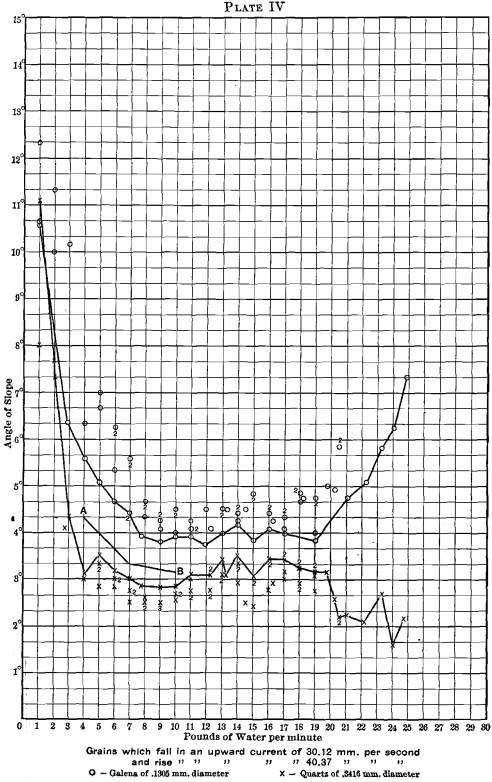
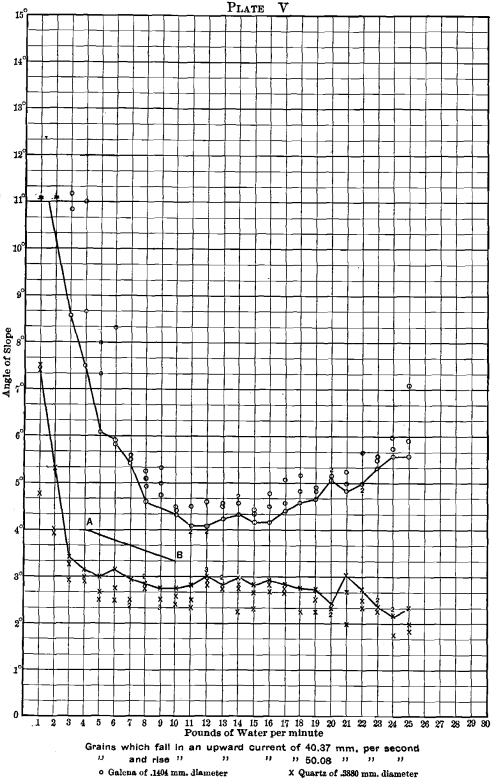
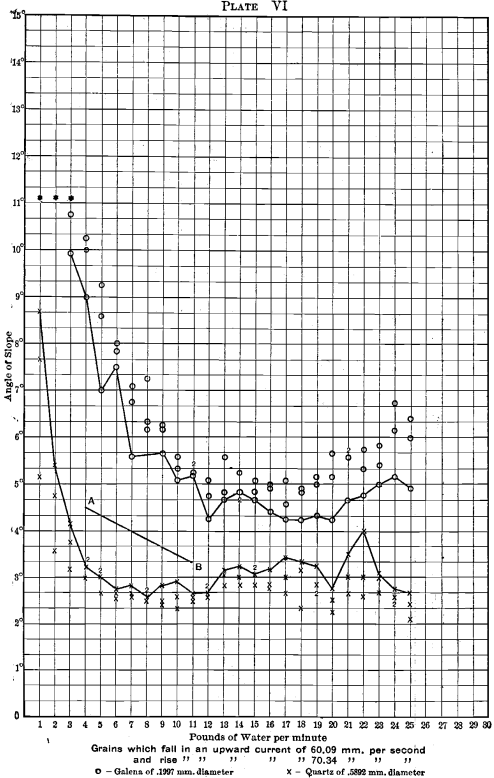
A few representative examples of the finish-angles of quartz and galena are plotted in Plates I. to VI. The vertical dimension (ordinate) gives the angle of slope; the horizontal dimension (abscissa) gives the amount of water per minute for 2 feet of width. The sizes of the grains and the sorting currents that are selected for plotting are given in Table II.:
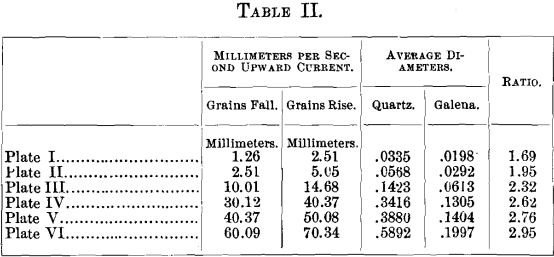
Three experiments were tried upon each water-quantity for each slime-sort, and the three readings are given upon the plates.
To aid in interpreting the curves, a line has been drawn joining the largest quartz-angles, and also the smallest galena-angles for each water-quantity.
The finish-angles of galena have been erased from Plates I. and II. for values of water above 8 pounds, since great difficulty was
experienced in eliminating the personal equation so as to obtain satisfactory values for these two plates. The difficulty lies in the fact that the bulk of the galena went off at very low angles, while a few grains hung on till the angle was extremely large.
Grains that are finer than those shown upon Plate I.—namely, slime-sort which rises in currents from 0. to 1.26 millimeters per second—give a very wide space between the quartz and galena for 1 pound of water; but the angles converge and meet at about 8 to 10 pounds of water; and with these and larger quantities of water all the grains of both minerals go off the table together at a little less than 2° slope.
Tables III. and IV. are taken from the curves and show the minimum galena finish-angles and the maximum quartz finish-angles of the three experiments in each case.
Water-Films
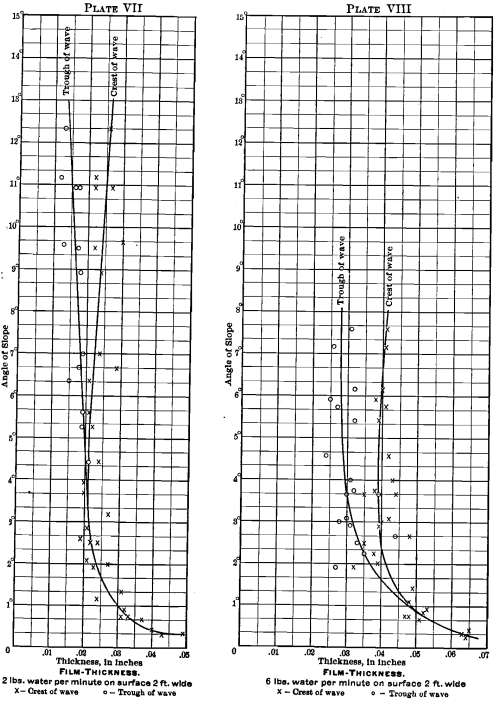
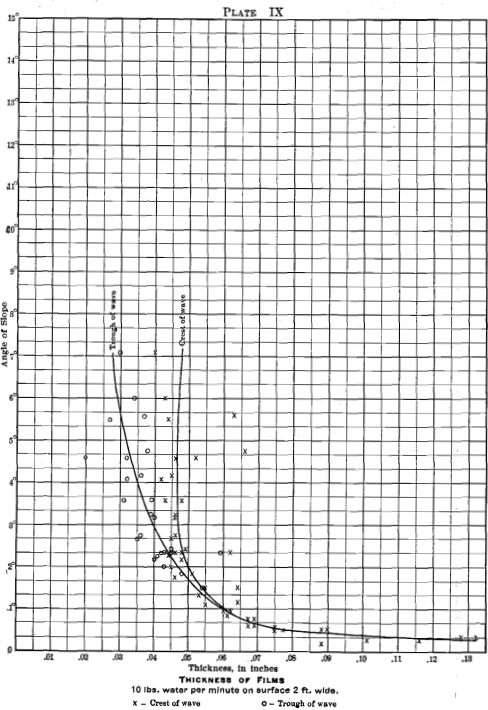
Plates VII., VIII. and IX. are examples selected out of the fifteen plates which were drawn to get average
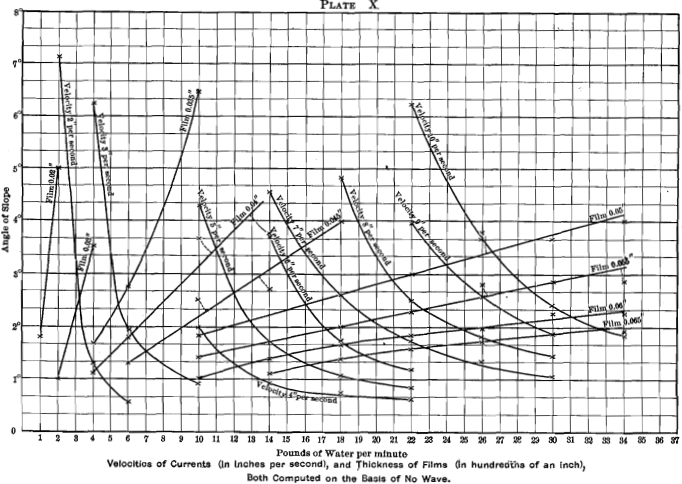
values for the thickness of water-film. Each plate represents a single rate of water-feed, and has all the film-thicknesses recorded for that weight of water. From these observations average curves are drawn, and each point on the curves represents : (1) the thickness of film (abscissa) which the given quantity of water will have with any angle of slope (ordinate); (2) where waves form, the angle at which the tendency begins is shown; and (3) the average heights of both crest and trough are given. These film-thicknesses are considered important aids to interpreting the effects of the finish-angles of Tables III. and IV. and Plates I. to VI. The complete set of values of these film-thicknesses is given in Table VI. Curves of water-thickness are also given on Plate X. These latter values are calculated from the figures given in Table VI. by assuming
that the mean thickness of the film is one-third the way from the thickness of the trough to the thickness of the crest.
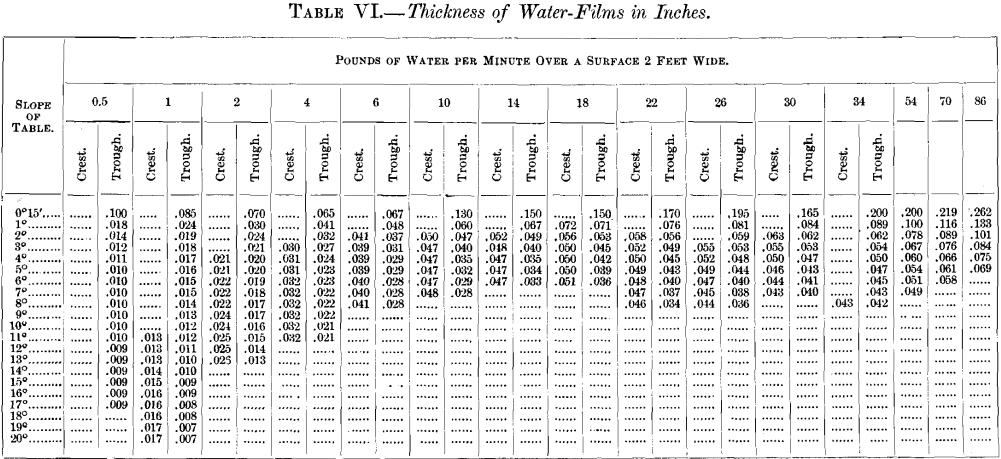
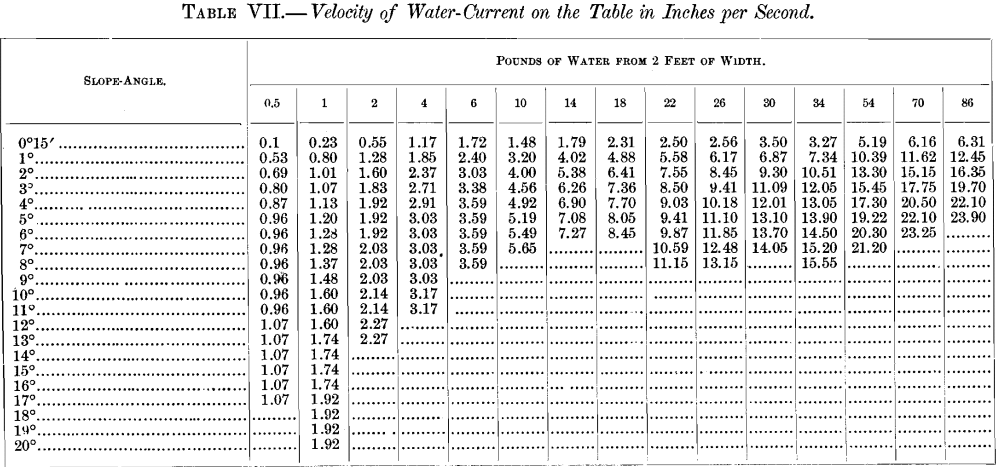
Velocity of the Current.—The velocity of the water-current (see Table VII. and Plate X.) is computed upon the assumption that the average thickness of film is one-third of the way between the thickness of the trough and that of the crest. These velocities will have a bearing upon the carrying-power of the water, and, therefore, upon the work of the slime-table.
Waves.—The tendency to form waves is best shown in Plate XI. The lines marked 10, 15, 20 per cent, and so on trace out that part of the field where the wave is elevated above the trough to a height of 10, 15, 20 per cent, and so on, of the thickness of the trough. Plate XI. was prepared from fifteen plates, of which Plates VII., VIII. and IX. are three, and from Table VI. This is an exceedingly interesting plate. It explains much that happens upon a table.
Conclusions
Preliminary Classification
Custom in this country has very nearly abolished classification of slimes. In some instances the overflow of the last hydraulic classifier is sent to a Spitzkasten apparatus with two or three pointed boxes, the product from each box going to its table; but it is more common to send these slimes to a distributing-tank, which sends whole slime to each of the tables, all of which are fed alike with a like quality of slime.
Is this wise ? The author is of the opinion that it is not wise, for the following reasons: Practice employs 6 to 14 pounds, or an average of about 10 pounds of water per minute on every 2 feet of width. This quantity washes away with the tailings the whole of the first slime-sort shown in Tables III. and IV. on any slime-table that has a slope of 0.42 inch or more per foot, while, in fact, there is scarcely a table in the United States that has less than ¾-inch slope to 1 foot. Again, upon a glance across Table IV., it is noticeable that heavier slime- sorts are not suited to the same angle as lighter slime-sorts with the same water.
Quartz and Galena-Curves
In Plates III., IV., V. and VI. the quartz-curve, passing from left to right, first drops somewhat, then bends round to nearly horizontal, diminishing a little as the water increases, and, except for the sudden fall at the left, it is nearly straight.
The galena-curve behaves very differently. It begins quite high up on the left, falls down rapidly as the water increases, then assumes a horizontal direction, and finally rises again to a considerably increased angle with large quantities of water.
Two questions arise, both of which are of interest in ore-dressing : 1. What is the cause of difference between the quartz- and galena-curves ? and 2. To what conclusions does it point ?
First, as to the cause. Referring to Plate XI., one sees that the tendency to form waves almost exactly corresponds to the galena curves (see Plates III., IV., V., VI.), that is to say, where the waves form freely, there the galena moves with a low angle. The higher the wave, the lower the angle at which the galena moves. This tendency of the waves to hurry the galena off the edge of the table, under the conditions here considered, suggests harm to the table-work. The waves might not be a hindrance to the ore-dresser if the quartz were affected in the same way as the galena. This, however, is not the case; the quartz is all washed off the table at an angle of slope at which the waves are slight, or do not exist at all. On this account the quartz does not show a corresponding dropping of the angle with that shown by galena. It is quite fair to presume that, if some way could be devised of killing the waves, galena would have a curve far up in the steep angles and parallel with the quartz all across.
Secondly, to what conclusions does this curious phenomenon point? The wider the interval between the quartz and the galena, the better would the field appear to be for treatment. If, for instance, all the quartz can be washed off while all the galena can stay at rest upon the table, then the results should be of the best. Now, there are two areas where the curves recede from each other. One is in the small water-quantities (2 pounds to 6 pounds), the other is out towards 20 and 25 pounds. These two areas point out two places of good treatment. The 25- pound area may be ruled out on account of the large quantity of water needed, unless there be special cases or special designs made which will enable the large quantity of water to treat also a large quantity of ore and so justify its adoption. We are left then for the most work to the small water area from 2 to 6 pounds of water, more or less, and to quartz-angles that are a little steeper in this part of the field.
Criticism may be directed towards the fact that these tests have been made with a plane table, whereas most of the wash-
ing is done upon convex conical tables. In reply it may be said that the convex table has a speed of flow and a thickness of film diminishing from the center towards the circumference, but the amount of change is very slight for 1 foot of distance when near the circumference of the table. If, therefore, the water be adjusted to give the quantity desired for the space, say from 1 to 2 feet from the margin, the conditions should be found there to be practically the same as on the plane table. No matter what may have happened higher up the slope, when the grains reach this foot of surface they should obey the law and stop or roll according to their size, the degree of slope and the amount of water.
Slope Angles & Water Quantities of Best Treatment
To bring the results down to a practical basis a line A B of “ best treatment ” has been drawn upon each of the Plates I. to VI. Somewhere upon this line, in the author’s opinion, will be found the best treatment for the particular slime-sort. The water-quantities and slope-angles for the two points A and B are given in Table V.
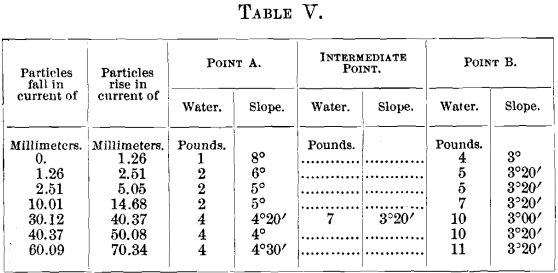
These slime-sorts can be grouped together into three classes :
I. Particles which fall in 30 mm. and rise in 70 mm. per second current.
II. Particles which fall in 1.26 and rise in 30 mm.
III. Particles which rise in 1.26 mm.
If these three great groups are adopted they will probably each be found to contain particles sufficiently near each other in behavior to be treated alike.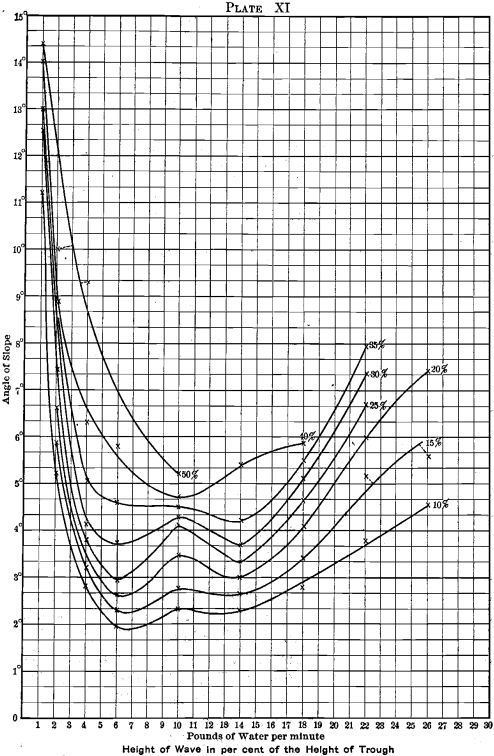
The plates clearly suggest a small quantity of water and steeper slopes for finer products, and a large quantity of water and gentler slopes for coarser products. The author has already seen, in the course of these experiments, indications that, in products which are well sorted, galena and quartz are susceptible of separation by large water-quantity and flat slope, even when the quartz is as large as 10-mesh.
Present and Proposed Practice Compared
Present practice uses tables ranging in slope from ¾ inch to 1½ inches to the foot. It also uses quantities of water for 2 feet of width that range from 6 pounds to 14 pounds. If we put the average at 10 pounds and consider a table with 1½-inch slope to the foot, then comparing Tables III. and IV. and also Plates I. to VI. we see that both the quartz and the galena are moving for the edge of the table. They are, in fact, racing and the quartz is winning the race.
A table with ¾-inch slope to the foot, and with 6 to 7 pounds water would be, for some slime-sorts, within the author’s figures; and the galena would be largely at rest upon the table, with the quartz departing from it. We may compare the two methods then by the two words “ racing ” and “ departure.” Most of the tables at present used are working in the portion of the field where the quartz and galena curves are closest together, and would seem therefore least advantageously placed. They are able to do this, because they are working upon the “racing” principle. The method of departure which the author suggests selects its area where the curves are far apart, where the galena may easily be put to rest upon the table and the quartz roll away and leave it behind.
Thus far, in this comparison, the ground has been taken that slimes should be sorted with a positive hydraulic and that an angle slightly larger than the quartz finish-angle is the right one to use, and the inference might be drawn that the writer condemns all the tables at present used. It would not be fair to the present practice or to the writer to close this paper without further reference to this point. The present plan uses the Spitzkasten, or the settling-tank, to distribute pulp to the tables. With the former the coarser slime-sorts have with them finer slime-sorts which the tables throw wholly away; with the latter all the tables have fine slime-sorts which they throw away. Both systems usually send to waste the overflows, which may contain quantities of valuable ore.
The mill-man has had in his possession no remedy for this throwing away of so much fine ore. In the first place, he has had no device for preventing the great volume of water from coming to this point, and no better way of handling it has been devised than to settle out what could be settled quickly, to treat it on a table, saving what could be got and to let the rest go.
A proposition, then, which asks for positive hydraulic to really classify the slimes, and does not diminish the quantity of the water until the last slime-sort is reached can hardly find favor unless it also suggests a way for diminishing the great quantity of water coming to this point. The author thinks this can be done by diminishing the number of ordinary hydraulic classifiers. They are all great diluters, and simply add water at that point which is to rob the treatment of large quantities of fine slimes, which must be lost in consequence.
Why cannot the European limit of 1½ mm., or even finer holes, for the last trommel be adopted ? One mill now operating in the United States is sifting down to ½ mm. and jigging the last-sized product with very clean tails—cleaner, in the author’s opinion, than those of jigs which are treating separator- spigots, except, perhaps, those run on the Lake Superior basis, with finishing jigs below.
The author believes that if our mills should use more trommels, carrying the sifting to a much finer point than at present, the tailings of the fine jigs would be cleaner and the systematic concentration of slimes possible.
The overflow of the Spitzkasten, or the distributing-tank, should not go to waste. It should all go over tables with suitable slope, water-quantity and speed.
Shaker Table Speed
It will be clear that with the gentler slopes and water-quantities proposed by the author the tables must also move more slowly to give time for the quartz to roll off. Instead of the present speed of one revolution per minute for a 17-foot table the speed must be diminished to one revolution in three minutes, five minutes or even more, as the work in hand demands.
The more the subject is studied the more intricate it seems to be; and when one hears that the slime-table has been tried at this place and at that, has proved a failure and has been thrown out, one is inclined to think that its principles were not understood, and that with a better knowledge of the apparatus such cases would be rare.
I wish to give credit to Messrs. William A. Tucker, Charles D. Demond and B. Stoughton for the good work they have done in the experimental part of the preparation of this paper.
