It is often necessary to calculate the size of a mine hoisting system required to raise a given quantity of material, either as a preliminary to the detail design of the machinery, or to decide whether machinery on hand or offered by a manufacturer is adapted to the work to be done.

The first element of the problem to be determined is the load to be raised. In a mine that is already developed, this is limited by the size of car that can be hoisted out of the mine and that will pass through the underground gangways. If these place no limits on the design, the size of the load will depend on the output desired per day, and on the number of hoists that can be made per day. The latter are fixed by the time required per hoist and the number of hours available for hoisting, after deducting from the working-day the time required for raising and lowering men, sending down supplies, and for the many small delays in handling cars. It must also be decided whether the hoisting is to be done in one shift or in all of them.

As an example, assume an output of 400 tons per 10 hours; shaft, with two compartments, 1000 ft. deep; hoisting in balance ; time available for hoisting, 6 h.; engine can hoist load in 1.5 min., and time to change cars 0.5 min. (the change at top and bottom of shaft being made at the same time). Then, 30 cars can be raised per hour, or 180 cars in 6 hours. This would require cars of 400 ÷ 180 = 2.22 tons capacity, to handle the desired output.

With a single shaft, the time to raise one load is the time to change or load cars at the bottom, hoist loads, change cars or dump at the top, and lower the empty cars; while, in a double shaft, two cars could be handled while the above programme was being carried out in a single shaft, as the second load would be raised while the first empty was going back down, and changing of cars at the top and bottom would be going on simultaneously.

Ropes

Having settled the size of the useful load to be hoisted, the size of the rope must be determined. This must be strong enough to hoist the total load, including its own weight, and to withstand the starting-stresses due to picking up the load suddenly when the rope is slack. Experiments have shown that, in starting with six inches of slack rope, the stress in the rope is about double that due to picking up the load gently.

Expressing these stresses in a formula, let

K = stress in rope in pounds, at the head sheave, at the instant of picking up the load.
W = weight of gross load in pounds.
R = weight of rope in pounds.
F = friction in pounds = weight of all moving parts multiplied by f.
f = coefficient of friction.

Then K = 2 W+ R + F…………………………. (1)

This stress should not exceed 1/7 of the ultimate strength of the rope. The coefficient of friction, f, may be taken as .01 for vertical shafts, and as .02 to .04 for inclined shafts with rope well supported on rollers.

As an example, required to find size of rope necessary to hoist a total load of 5000 lbs. from a vertical shaft 1500 ft. deep. Assume, for a trial solution, that rope weighs 2 lbs. per ft. From equation 1, K=5000 lbs. X 2 +1500 X 2 lbs. + .01 X 8000 lbs. = 13,080 lbs., and ultimate strength of rope should be 7 X 13,080 =91,560 lbs., which would require a 1¼-inch- diameter flexible cast-steel rope, having an ultimate strength of 100,000 lbs., and weighing 2.45 lbs. per ft. This weight would increase R in above equation, and make 7 x K = 96,285, which is still less than the ultimate strength of the rope chosen. If a rope of lighter weight is desired, a plow-steel rope could be used instead of the cast-steel.

If the shaft is inclined, the stress in the rope due to the weight hoisted will vary with the sine of the angle of inclination, thus:

K = (2 W + R) sin x + F,……………………………………. (2)

in which x is the angle of inclination. Here the friction is also affected by the slope, and varies with the cosine of x, or F = f (W+R) cos x; f may be taken as .02.

In the following discussion the loads will be considered as being hoisted from vertical shafts, as the principle remains the same for both classes, the only difference being that the stresses in the rope and on the engine and other parts of the machinery change with changes in the slope.

Drums

The minimum diameter of the drums is determined by the size of the rope used, and the larger the drums the smaller will be the bending-stresses and the more strength will be available for useful work.

Mr. William Hewitt has shown that, when the diameter of the sheave or drum is 44.5 times the diameter of a 19-wire cast-steel rope, the bending-stresses are 2/3 and the remaining useful strength is 1/3 of the “ maximum safe load ” that the rope will carry. The “ maximum safe load ” is taken as 1/3 the ultimate strength. This is well below the elastic limit of the wire. Thus the available strength is only 1/9 of the ultimate. In order to cut down the bending-stresses so as to leave of the ultimate strength of the rope available for useful work, the sheaves must be about 80 times the diameter of the rope. Other grades of rope require different diameter of drums, as will be seen by studying Tables I. and II.

Table II. is based on the formula k = Ea/2.06 R/d + C in which

k represents the bending-stress in pounds, E the modulus of elasticity = 28,500,000, a the aggregate area of the wires in square inches, R the radius of the bend in inches, d the diameter of the individual wires in inches, and C a constant depending on the number of wires in the strand. The values of d and C are, for 19-wire hoisting-rope : d = 1/15 diameter of rope, and C= 45.9.

As an example, required the working-load of a 1-in. cast-steel rope running over a 6-ft. sheave. From Table II. the bending-stress is found to be 9937 lbs., and from Table I. the “ maximum safe stress ” is found to be 22,667 lbs. The difference, 12,730 lbs., is the working-load.

The size of the rope fixes the minimum diameter of the

drum, but questions of speed and length of drum also influence the final choice of the diameter.

The maximum length of a drum, aside from question of room, is controlled by the allowable fleet-angle, that is, the acute angle included between two lines drawn from the ends of the drum to the head sheave. This angle should not exceed 6°, in order that the rope may lead well on to the head sheave, and so that one rope will not grind or mount the next one in winding onto the drum. It is usual to place the drum far enough back from the head sheave to keep the fleet-angle within the limit; but where it cannot be done, it is necessary to guide the rope onto the head sheave and onto the drum by rollers or sheaves running on vertical spindles. The bisectrix of the fleet-angle should strike the middle of the drum.

Types of Hoisting-Engines

Single-cylinder engines are used in mining to replace man- or animal-power for light work.

They are always geared and provided with a flywheel on the crank-shaft. They must be started to a fair speed, in order that the fly-wheel may develop sufficient momentum to carry the crank over the center, before the friction is thrown in to pick up the load. The cylinder should have 75 per cent, more power than is necessary simply to raise the load, in order that speed may be maintained.

Double-cylinder engines are used for all the regular work of mining. They may be divided into the following classes:

I. Geared:—Single Cylindrical Drum.
Double Cylindrical Drum.
Double Conical Drum.

II. Direct Acting:—Single Cylindrical Drum.
Double Cylindrical Drum.
Double Conical Drum.
Koepe System.
Reels for flat rope.

Each of these has a field of its own to which it is best adapted. Thus, the geared engine is used mostly for shallow depths and small outputs per day, while the direct-acting engine is used where the output is large. There are many cases near the dividing-line in which either type of engine will give equally good results, and it is largely a matter of personal choice as to which is used.

Geared engines are made with small cylinders, and the engine proper runs at a speed of 100 to 200 r. p. m. The gearing usually gives a reduction of 1/3 to 1/5 so that the drum revolves at a moderate speed. The small cylinders make the first cost lower than that of a direct-acting engine; but the gearing for large hoists is a serious objection. The main gear has about the same diameter as the drum, so as to keep the pressure on the teeth as low as possible; and hence it has a circumferential speed equal to the speed of hoisting. Gearing, under very favorable conditions, should not run at a speed over 1200 ft. per min., and with the large cast gears and the rough work to which hoisting-engines are subjected, the speed should probably not exceed 900 ft. per min. If the average speed of hoisting is kept at about 2/3 of this maximum, the average speed will not exceed 600 ft. per min. This speed will allow the use of moderate-sized drums and keep the piston- speeds within the limits of good practice.

That gearing is liable to cause trouble and make considerable noise when run at a high speed, has been forcibly impressed on the mind of the writer by his experience in charge of a geared hoister, made by a reliable manufacturer, having cylinders each 18 in. dia. by 24 in. stroke, and two drums, each 7 ft. 6 in. dia. by 5 ft. face, on which three main gears, between 7 and 8 ft. dia., 3 in. pitch, and 9 in. face, were broken inside of nine months. The gears cost about $3000 each, besides the labor of replacing and the loss of 24 hours in changing the old for a new one. The engine was hoisting from a shaft 1000 ft. deep in about 1¼ min. The load of ore was 2½ tons.

Direct-acting engines should not be used for hoisting-speeds of less than 500 ft. per min., as the piston-speed will be too slow for economy. They can readily be run at an average speed of 1500 ft. per min., and the largest engines can be run as much as 2500 ft. per min., if the shafts are deep.

Single-drum engines are limited to small outputs per day, or to places where the first cost of the plant is so important as to outweigh the loss in increased operating-expenses. This type of engine has many applications, as for sinking winzes, and for other inside work; also for shaft-sinking, and for working coal-mines on a small scale, where the cost of fuel is small, as waste material is burned. They are largely used in the Joplin, Mo., district, where the hoisting is from vertical shafts 100 ft. deep, the output often only 25 to 50 tons per day, and the ore is raised in buckets without guides, thus keeping the dead weight small, as compared with weight of ore raised. They are not adapted for regular mining work on a large scale, as the work expended in raising the cage, car and rope, each trip, would exceed the work of raising the ore.

Double-drum engines overcome the dead-work of hoisting the ore-carriers by balancing the weight of the cage and car in one compartment against those in the other. They are thus more economical to operate than a single-drum engine, and the cost of installing will probably not be over 50 per cent, greater than for a single-drum engine. The cost of sinking a shaft large enough for two hoisting-compartments and a manway is not much more than that of a shaft with only one hoisting-compartment and a manway; the head buildings must be nearly the same in either case; and the double-drum engine will have smaller cylinders, thus partly offsetting the cost of the second drum.

With cylindrical drums, the ropes in the two compartments, from the cages to the head sheaves, are of constantly varying lengths, and are in balance only when the cages are passing at the center. With double conical drums, the work on the engine is kept constant by giving the cage at the bottom the short leverage of the small end of the drum, and the cage at the top the longer leverage of the large end of the drum.

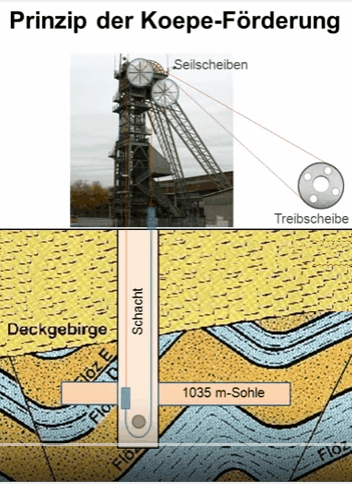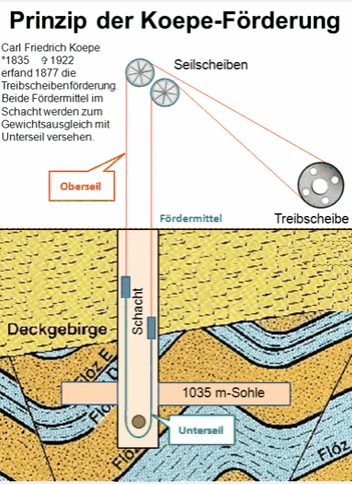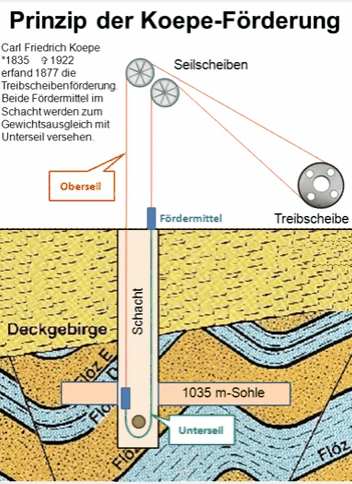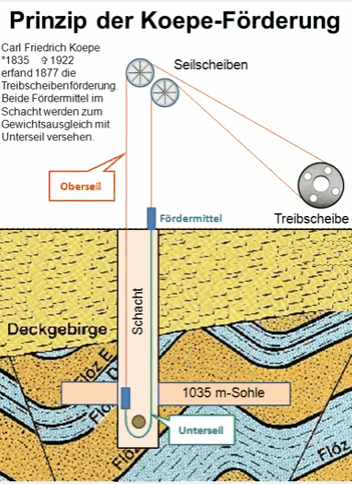
The Koepe system, as applied to a double-compartment shaft, has a tail-rope passing from the bottom of one cage down and around an idle sheave at the bottom of the shaft, and up to the other cage. Thus the weight of the rope in the two compartments is exactly equal, and the whole hoisting mechanism is in balance at all points of the trip.

The flat-rope system of hoisting attempts to equalize the work on the engine by coiling a rope of rectangular cross-section on a reel, like a surveyor’s linen tape; so that the diameter of the reel increases and the leverage of the load increases as the weight of the constantly shortening rope decreases. Thus the work on the engine is kept constant, when the rate of increase of leverage and decrease of weight are in inverse proportion to each other. The flat ropes, however, are heavier than round ropes of the same strength, are shorter-lived, and cost more at first and for subsequent care. The flat-rope system is very largely used in Montana, and in some other districts which have followed the Montana practice.

The peculiarities of the different types of engines are brought out more fully by the calculation of the size of their cylinders when equipped with the different arrangements of drums.

Calculation of the Cylinders

The maximum work on the engine is in picking up the load and in overcoming its inertia. At this time one crank may be on a dead center, so that all the work must be done by the other. At this part of the hoist, steam will be admitted for the full stroke and at its maximum throttle-pressure.

Hoisting-engines belong to the slow-speed type of engines. Their valves are simple slide-valves in all but the largest sizes, and then they are usually of the Corliss class. They seldom have governing-devices, their speed being determined by the hoisting-engineer by means of the throttle, the link-motion and the brake.

With these classes of engines the piston-speed may be taken at 200 to 400 ft. per min. for engines of 12- to 24-in. stroke,, and from 400 to 600 ft. per min. for those with 24- to 72-in. strokes. Very high-grade engines, with other valve-gearing, may run at higher piston-speeds.

At the instant of starting, the power in one cylinder acting on the crank, in the top or bottom position, must have a moment equal to or greater than the moment of the unbalanced load pulling from the circumference of the drum. After starting, the other cylinder comes in to accelerate the speed, and the two together are able to hoist the load with steam partially cut off and still maintain the full speed.

In all the following equations, let

W = weight of unbalanced load in pounds.
C = weight of cage and car,
O = weight of ore, and
R = weight of rope, all in pounds.
D = diameter of drum in feet.
P = M E P = mean effective steam-pressure in cylinder in lbs. per sq. inch.
A = area of cylinder in sq. inches.
L = length of stroke in feet.
S = speed of hoisting in ft. per min.
R = number of revolutions of engine per min.
F = friction in pounds,
f = coefficient of friction.
r = ratio of diameter of piston to length of stroke, both being in feet or both in inches, = stroke/diameter
d = diameter of piston in inches,
e = efficiency of engine.
g = ratio of gearing = diameter of gear/diameter of pinion

Then, for a single-drum, direct-acting engine, Fig. 1, the moment of the load = (W + F) D/2 and the moment of the engine = (P x A x e)L/2. Placing these equal to each other,

(W + F) D/2 = (P x A x e)L/2…………………………………….(4)

If the drum is geared, the engine will make g revolutions to one of the drum, or the leverage of the engine is increased to g times what it would be if directly connected, and the equation becomes

(W + F) D/2 = P x A x L x e x g/2………………………………….(5)

This is the general equation for all hoisting-engines. If they are directly connected, the ratio of gearing, g, equals 1.

https://www.youtube.com/watch?v=l7-ju2b4h2U

When the weight of the load, size of the drum, and steam pressure are given to determine the size of the cylinders, there are two unknown quantities in the equation, viz.: A and L. Here L can be assumed and the equation solved for A, from which the diameter can be obtained. The usual practice is so to proportion the cylinder that the length of travel is 1¼ to 2½ times the diameter of the piston. If the value of L chosen for trial gives a ratio of stroke to diameter outside of these limits, another value must be taken for L, and another solution made. If the ratio is decided upon first, then the area can be expressed in terms of the stroke, and there is only one unknown quantity in the equation. Thus rd =12L or d = 12L/r (12L being the length of the stroke in inches), and A = π d²/h = π x 144L²/4r²; which substituted in equation 5 , gives

Having obtained the size of cylinders, and knowing the speed of hoisting and size of drum, the speed of the engine can be obtained, and the speed of the piston can be investigated. The speed of hoisting, in feet per min., divided by the circumference in feet, will give the number of revolutions of the drum per minute. If the drum is geared, the engine will make g times as many r. p. m. (revolutions per minute) as the drum, and

N = S/πD x g……………………………………(7)

The piston-speed in feet per min. = 2L x N, or

Piston-speed = 2LS/πD x g………………………(8)

Where the engine is direct-acting, g = 1 in both equations, 7 and 8.

The horse-power available for hoisting when the engine is running at full speed will be expressed by the formula :

H. P. of engine = P x L x A x 2N/33000 x e………………………….(9)

and the horse-power required to raise the load will be:

H. P. of load = (W + F) S/33000…………………….(10)

In the examples here given the weight of the car is taken as 2/5, and the weight of the cage as 3/5 of the weight of the ore hoisted. These together make the dead load, C, equal to the weight of the ore, O. These are sufficiently close to the usual practice for an illustration of the method of using the formulas.

As an example, take a double-cylinder engine geared to a single drum, to find the size of cylinders required under the following known conditions : Vertical shaft is 400 ft. deep, cage to be hoisted in one minute; the-weights are, cage 900 lbs., car 600 lbs., ore 1500 lbs., rope 400 lbs.; steam pressure, P, is 60 lbs., e = 0.7, g = 4/1, f = .01 (assumed), D = 4 ft. and L may be taken as 1½ ft. for a trial solution; then,

The stroke, L, was taken as 18 inches for a trial solution, and this gives a well-proportioned cylinder, viz., 8½ in. in dia. x 18 in. stroke.

The speed of the piston can be tested by equation 8:

Piston-speed = 2LS/πD x g = 2 x 1½ x 400 x 4/3.1416 x 4 = 382 ft. per min.

which is within the limits for these engines.

From equations 9 and 10 combined, the mean effective-pressure required in the cylinders to perform the work can be determined. Substituting the known values in these equations, placing one equal to the other, and solving, we have

which, with 60 lbs. at throttle, corresponds to a cut-off of about ½. As both cylinders are in use, the area has been doubled in the above calculation.

With double-drum hoisters, where the descending cage and car counterbalance the ascending ones, the general equation 5 still applies, but the value of W and F are changed. Referring to Fig. 2, when a loaded car is to be started from the bottom of the shaft and an empty car is being lowered at the same time,

W= (R + C + O) — C = R + O, and
F = (R + 2C + O)f,

which values must be used in the first member of equation 5.

As an example, take a hoister raising a load from a double-compartment shaft 2000 ft. deep in one minute : O = 5000 lbs., C= 5000 lbs., R = 6000 lbs., D = 8 ft., P = 60 lbs., engine directly connected (hence g = 1), f = 0.01, e = 0.7. Taking L = 4 ft. for a trial and substituting in equation 5 to find the size of cylinders,

This gives a cylinder 26 1/8 in. in diameter by 48 in. stroke.

Determining the piston-speed by equation 8,

While the proportions of the cylinders follow the usual practice, the piston-speed exceeds the limits previously set for this class of engines, viz., 400 to 600 ft. per min. This speed can be reduced by choosing a smaller value for L in equation 5, which will give a cylinder larger in diameter. Thus, if the length had been taken as 44 in., or L = 3 2/3 ft., d would have been 27¼ in., and the ratio 12L/d = 1.6+, and the piston-speed = 584 ft. per min.

Or, instead of shortening the stroke, the number of revolutions can be cut down by increasing the diameter of the drum; thus, if D = 9 ft. and L = 4 ft., d will be 27¾ in., the ratio 12L/d = 1.73, and the piston-speed = 566 ft. per min.

Conical drums, as already noted, are intended to equalize the varying load on the engine, due to the change in length and weight of the rope as the cage ascends and descends. As these engines are used where every economy is desirable, they are usually direct-acting and fitted with double drums.

The minimum diameter of the drums is determined by the size of the rope.

Referring to Fig. 3, let D represent the small diameter of the drum in feet;

y = diameter of large end of drum in feet.
C = weight of cage and car in pounds.
O = weight of ore in pounds.
Rl = weight of the long length of rope when cage bottom of the shaft.
Rs = weight of the short length of rope when cage top of the shaft.
Then,

(C + O + Rl) D/2 – (C + Rs) y/2 = moment of the resistance when the load is at the bottom, Fig. 3, position A, and (C+O+Rs)y/2-(C+Rl)D/2 = moment of the resistance when the load is at the top, Fig. 3, position B. The object of the conical drums being to keep this moment constant, these two values must be equal, and

(C + O + Rl)D — (C + Rs)y = (C + O + Rs)y — (C + Rl)D…………(11)

Solve for y. Then, taking either end case, say when the load is at the bottom, the moment of the resistance of the loads, with friction added, must equal the moment of the power of the engine. This, following the same form as equation 5, gives:

Taking as an example the one used for the engine with double cylindrical drums, depth of shaft 2000 ft. plus 33 1/3 ft. to head sheave above landing, S = 2000 ft. per min., O = 5000 lbs., C = 5000 lbs., Rl = 6100 lbs., Rs. = 100 lbs., D = 7 ft., P = 60 lbs., g = 1, f = .01, e = 0.7, L for trial = 4 ft., to find diameter of cylinder.

From equation 11,

(C + O + Rl)D — (C+Rs)y = (C + O + Rs) y — (C + Rl) D, (16100 x 7) — (5100 y) (10100y) — (11100 x 7),

whence, y = 12.52 ft. = diameter of large end of drum.

Substituting in equation 12,

D being taken here as the mean diameter.

There must be a division left between the ropes on a conical drum in order to furnish positive grooves for the rope, so that the large coils cannot slip down over the smaller ones; hence the drum must be longer than those of the cylindrical design, even when the mean diameter of the conical drum is the same as the diameter of a cylindrical one.

In the Koepe system, as applied to a double-compartment shaft, there is a tail-rope of the same weight as the hoisting-rope fastened to the bottom of one of the cages, passed around a sheave in a pit at the bottom of the shaft, and attached to the bottom of the other cage. Then, in whatever position the cages are in the shaft, there is the same weight of rope hanging in each compartment. Thus the entire weight of the hoisting mechanism is in perfect balance at all times, and the engine only has to raise the weight of the ore and overcome the friction of the moving parts. The main rope may be wound on a pair of cylindrical drums, or it can be wrapped back and forth over a pair of multiple-grooved sheaves, as is done in rope drives for many purposes. It is essential that a positive grip is taken on the rope by the driving mechanism, or else its creeping on the driving-sheaves will make the indicators show a false position for the cages, and make accidents of overwinding a great, source of danger.

The calculation of the size of the engines required can be made by equation 5. The engines would usually be direct-acting.

As an example, assume the same conditions as have been used before:

S = 2000 ft. per min. O = 5000 lbs. C = 5000 lbs. R = 6000 lbs. P = 60 lbs., e = 0.7, f = 0.01, g = 1, D = 8 ft., L = 4 ft., for trial.

This is a rather small diameter for a cylinder of this length, as its length is 2 2/3 times the diameter, which exceeds the ratio already recommended. If L were taken as 36 inches, the area would be 335 sq. in., corresponding to 20 5/8 in. diameter, which gives a cylinder with better proportions.

The piston-speed can be obtained from equation 8, and the mean effective-pressure required, when hoisting at full speed, can be found from equations 9 and 10 combined.

It is interesting to compare the sizes of the three types of engines, hoisting the same load at the same speed. These tabulated are:

The conditions in all of the above were the same as used in former examples, except that the diameters of drums are all taken as 9.76 ft., which is the mean diameter of the conical drums. The engines are direct-acting, the shaft has double compartments, and the cages work in balance; C =5000 lbs., O = 5000 lbs., R = 6100 lbs., P = 60 lbs., L = 4 ft., f = .01, e = 0.7, g = 1, S = 2000 ft. The piston-speed is 522 ft. per min. in each case.

The table shows that cylindrical drums are not as economical to operate as either the conical drums or the Koepe system. The conical drums are expensive to make, as the grooves have to be formed spirally and with an increasing radius, and each problem requires a specially-designed drum, so there can be little use made of stock patterns. They are only used where the rope is heavy, and the economy of accurate counter-balancing is clearly indicated, and will offset the extra cost of manufacture.

The Koepe system is a simple method of counter-balancing, and the principle could often be applied to existing plants with cylindrical drums by adding a tail-rope and an idle sheave at the bottom of the shaft, provided there is sufficient sump-room for the sheave and its slide. The objection to the Koepe system, where used without drums, is the liability of the ropes to creep on the sheaves, causing the indicators to give a false record and so increase the danger of overwinding.

Flat ropes of rectangular cross-section are wound on a reel like a tape. When the load starts from the bottom of the shaft the rope winds on the center of the reel, which is of small diameter, and then, as the load rises, the successive layers increase the diameter of the coil on the reel; thus the leverage of the load increases and the weight decreases. If the original diameter of the barrel of the reel and the thickness of the rope are properly chosen, the moment of the resistance will be constant.

The proportions of the reel can be found as follows :

Let D = diameter of the barrel in feet.
y= diameter of coil of rope, when cage is at the top, in ft,
C = weight of cage and car, O = weight of ore, and R = weight of rope, all in pounds, as before.
l = length of rope or depth of shaft in feet,
t = thickness of rope in inches,
n = number of layers of rope in coil.

Then, referring to Fig. 4, y + D/2 π x n = l, and (y – D)12/2t = n.

Substituting the latter value of n in the first equation gives

From equation 13, knowing t, the value of y can be obtained, or having decided on y, the equation can be solved for t. The minimum diameter of the barrel, D, depends on the thickness of the rope, and can be calculated from Mr. Hewitt’s equation, previously given : k = Ea/2.06 R/d + C in which k= bending-stress in pounds, E = modulus of elasticity = 28,500,000, a = aggregate area of the wire in sq. in., R = radius of the bend in inches, d = diameter of individual wires, and C a constant depending on the number of wires in a strand. With flat rope, d = 1/6 the thickness of the rope, and C = 27.54.

The moment of the resistance at starting the load would be the moment of the weight, C + O + R plus the friction, acting with the lever arm D/2 as in equation 5.

The ideal case would be one in which the work of hoisting was constant at every part of the hoist; but the thickness of the rope may be such that the leverage of the load increases faster or slower than the weight of the load decreases, thus making the work on the engine to vary daring the trip. In such a case, the design must be tested with the cage at various points, to make sure that the engine has sufficient power to handle the loads at the desired speed at all points. For this, equations 9 and 10 may be used.

Generally these hoists are arranged in pairs, so that one cage ascends while the other descends. Then the necessary large diameter of the reel, to make the work constant on the engine, can be found by equation 11, used for conical drums, and the size of the engine from equation 12. After this the thickness of the rope can be found by equation 13.

If the reels cannot be made of such diameter as to make the work of hoisting uniform throughout the trip, with a reasonable thickness of rope, then the case must be considered by itself, and the design must be tested with the cage in positions sufficiently numerous to prove that the engine that will start the load is strong enough to handle it at all points.