H. J. Kamack (E. I. du Pont de Nemours & Co., Inc., Wilmington, Del.)—Rittinger’s law usually is stated to the following effect: “The work (or energy) consumed in particle size reduction is proportional to the new surface area produced.” The law has been stated substantially in this way by Taggart, Berry, Dalla Valle, Coghill and DeVaney, Richards and Locke, Gross and many others, and, according to Gaudin was originally expressed by Rittinger in the same form. Consequently there can be little doubt that this is the understanding of the law among most workers in the field of particle size reduction. Bond and Wang, however, express the law in the form the useful work accomplished. The distinction is critical, for in the form used by Bond and Wang the law becomes, as they themselves remark “merely a more or less arbitrary definition of useful work,” while in its usual sense the law expresses a physical hypothesis which has been verified experimentally within certain limitations.
Considering the way the law has been used, it might be stated more explicitly as follows: “In a given machine operating under a given set of constant operating conditions, the work consumed in the particle size reduction of a given material is proportional to the new surface area produced.” Or, as Coghill and deVaney have said, “the (Rittinger) law holds only when the tests being compared are made under analogous conditions.” There are occasions when the law transcends these limitations; for example, the surface area produced per unit energy consumption for a given material in a ball mill does not vary much over a fairly wide range of operating conditions. But by and large, the surface area production per unit energy consumption will vary with the operating conditions, the type of machine, and the material. The essence of Rittinger’s law is that the surface area production per unit energy consumption is independent of the particle size, and this has been verified experimentally by numerous workers for numerous materials, within certain limits. An important limitation is that when one grinds to very small particle sizes, agglomerative forces may tend to interfere with size reduction so that the surface area increases less rapidly than Rittinger’s law would predict. Within such limitations, Rittinger’s law can be regarded as empirically established.
Strain-Energy Theory: According to this hypothesis, the work consumed in size reduction of a particular material is proportional to (n + 2) (n — 1) /n, where n is the reduction ratio. This expression is approximately equal to n (the difference never exceeds 12.5 pct of n when n is greater than 1.66). When the cumulative size distributions of feed and product are nearly parallel, Bond and Wang define n as F/P, where F and P are the sizes which pass 80 pct of the feed and product, respectively. When the feed is closely sized, Bond and Wang describe a method for calculating an average value of n. In either case, it can be shown that n represents approximately the ratio Dr/Dp, where D denotes specific surface average particle size and the subscripts f and p refer to feed and product, respectively. D (in cm) is defined by the relation
D = 6/(SA) (Sp)
where SA is the specific surface area of the material in sq cm/g and Sp is its specific gravity.
According to the strain-energy theory, then, the work consumed in size reduction of a particular material is proportional to Df/Dp, while according to Rittinger’s law it is proportioned to
1/Dp – 1/Df
Consequently, if one starts with a given feed size, and comminutes until the reduction ratio is fairly large, both Rittinger’s law and the strain-energy law predict that the energy consumption will be inversely proportional to the specific surface average particle size of the product.
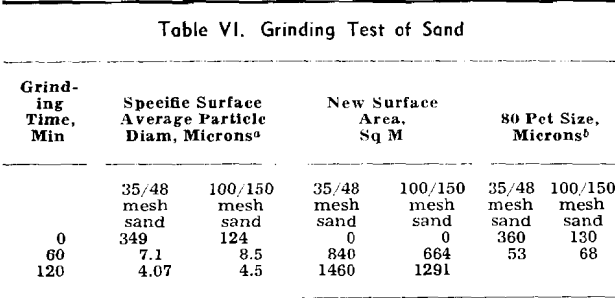
The arguments which Bond and Wang present against the Rittinger theory do not stand up under critical examination. The “strain-energy” theory which they propose instead is not supported by the empirical data they present and is disproved (for grinding) by an experiment which shows that for sand the energy required for grinding is not necessarily proportional to the reduction ratio.
F. C. Bond (authors’ reply)—The distinction between total work input and useful work accomplished in the statement of the first form of the Rittinger theory is important, since it is obvious that in a machine whose mechanical efficiency is different at different product sizes the work consumed in particle size reduction is not proportional to the new surface area produced; unless it should happen that the true relationship between useful work accomplished and surface area produced should compensate for the difference in mechanical efficiency. In a given machine operating under a given set of constant operating conditions the absolute mechanical efficiency is not necessarily constant at different feed and product sizes.
The power required to rotate a ball or rod mill when the feed is cut off is approximately the same as that required when grinding, and it is difficult to imagine that when 99 pct of the feed is cut off the relationship between energy input and surface area production remains constant.

