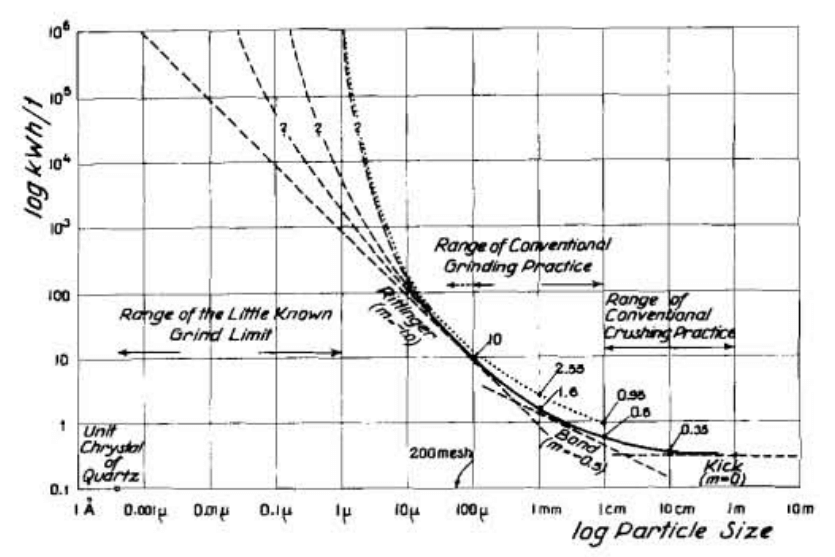
Many power-based grinding models exist, and most operators are familiar with Fred Bond’s “third theory”. Bond’s model is most commonly used to describe primary and secondary grinding to product sizes above, for example, 100 µm. Operators sometimes use Bond’s equation to describe grinding in situations where it is not appropriate, such as fine grinding below 50 µm. Using an alternative model would be a better choice in this situation.

Bond’s equation is one in a large family of models. Related equations better suited to fine grinding include the “signature plot”, Von Rittinger’s model and Charles’ equation. These models have a similar form to Bond’s and can be fit to industrial regrind mills and laboratory tests using the simple regression tools in the charts of computer spreadsheets. Operators will find that fine grinding calculations are both easier and more accurate when using the alternative equations to fit their regrind milling surveys or when performing laboratory regrind mill scale-up for plant design.

None of these models are new: Charles’ equation was published in 1957 and Von Rittinger’s model was proposed in 1867. A quick refresh how to apply these equations can turn these oddities from the undergraduate curriculum into useful tools for plant optimization. They can be fit to any type of mill including stirred and tumbling ball mills.