The purpose of this study was to measure the vapor pressure of silver as the first step in the determination of activities in silver alloys and to test the limitations of the method adopted. In order to work at low pressures, below 2×10-² mm of mercury, the orifice effusion technique was employed. To shorten the time of collection of silver from the atomic beam, radioactive silver (Ag110) was used as a tracer.
The rate of effusion of a monatomic vapor from an “ideal” orifice, where the thickness of the orifice edge is negligible compared with the orifice diameter, can be readily calculated from the kinetic theory of gases,
G = √M a p/√2πRT…………………………………………………….[1]
where G is the weight of material effusing from the orifice per unit time; p is the vapor pressure at oven temperature, T; R is the gas constant; M is the molecular weight of the vapor; and a is the orifice area.
Consolidating constants and expressing as the weight of material effusing from the orifice in a period of time, t,
GT = (5.83) (10-²) (√M) (a) (t) (p)/√T………………………………….[2]
where GT is total weight of monatomic vapor effused (g); M is molecular weight of the effusing tracer vapor; a is orifice area (cm²); t is time of effusion (sec); p is vapor pressure of effusing material (mm of Hg); and T is oven temperature (°K).
GT = Gθ/1 – cos²θ = Gθ/sin²θ……………………………………………….[3]
GT = Gθ (D² + 4d²)/D²………………………………………………….[4]
Gθ110 = CT/CS · Ws…………………………………………………[5]
To correct for difference in weights between Ag and Ag110, the factor √110/107.88 must be introduced if results are to be reported as the vapor pressure of the normal mixture of stable silver isotopes or
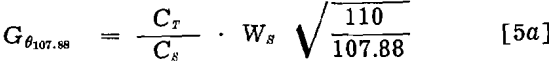
Substituting the equivalents for Gθ107.88 and GT and solving eq 2 for p107.88, the final equation is obtained,
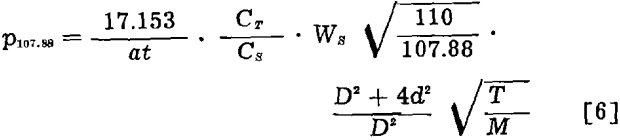
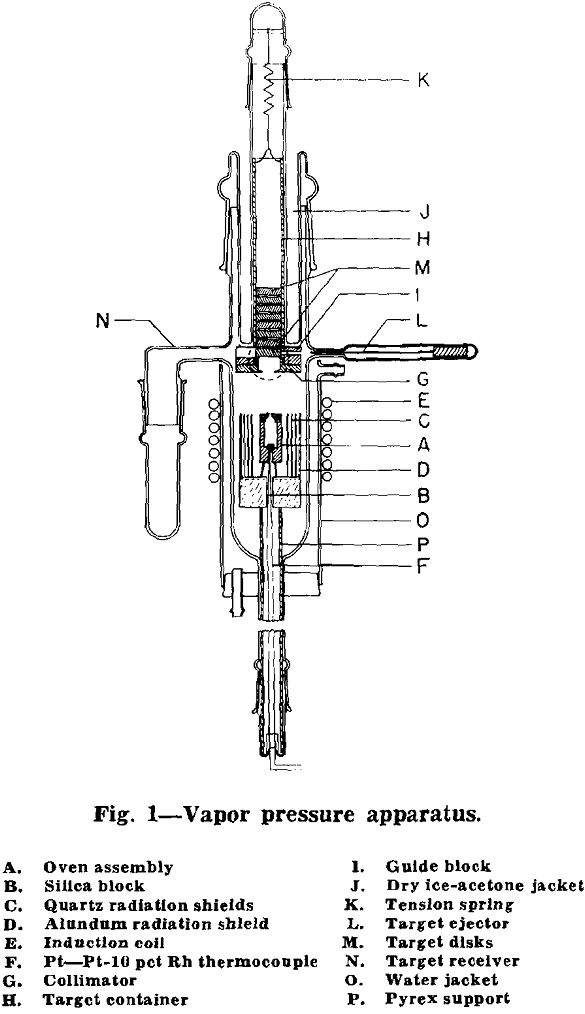
Apparatus
The oven assembly (A) consisted of a tantalum body containing the Ag + Ag110 covered by a nickel oven lid upon which was welded a 0.003 in. nickel orifice plate. Orifices were prepared from the nickel sheet by dimpling and then polishing the convex protrusion until a hole of the desired diameter was produced. The coolest portion of the oven, hence the effective temperature of the system, was that of the oven base where temperature measurements were made.
The oven was supported by three, pointed tungsten wire legs which rested in a conical hole, V-groove, and rectangular notch in the silica block (B). The cell was surrounded by three, concentric, clear quartz radiation shields (C), between which was placed 0.003 in. slotted tantalum sheet. An outer shield of alundum (D) surrounded the entire assembly. Heating of the oven was effected by the externally wound induction coil (E).
The oven charge was prepared by diluting 1/5 unit of radioactive Ag110 ( ≈ 7 millicurie) with 2.7 g of fine silver powder, Lot No. 4303-D of the U. S. Metals Refining Co. Since the radioisotope was received as AgNO3, it was necessary to precipitate Ag110 as the hydroxide and then decompose this to metallic Ag110 by heating.
Following melting to effect homogenization of Ag110 throughout the charge, a weighed sample was taken from the oven and dissolved in dilute HNO3. An aliquot part representing 18.8 micrograms of the oven charge was then evaporated upon one of the target disks for use as a standard.
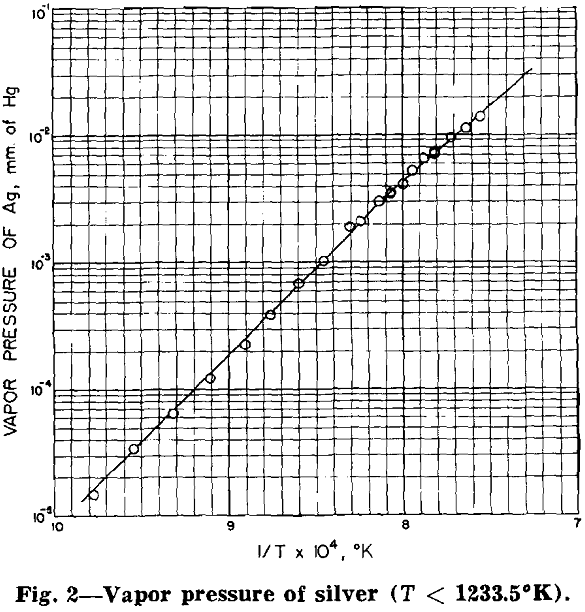
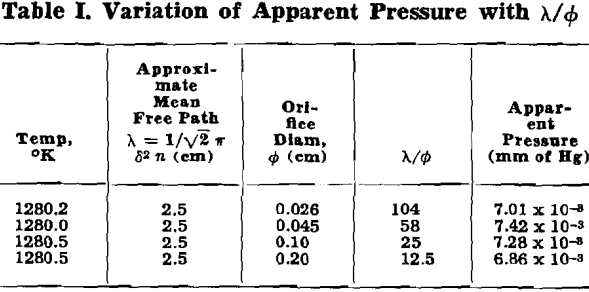
The geometrical conditions applicable to and the results of 21 target exposures, covering the temperature range 1023.6° to 1323.8°K, are given in table II. The methods of determining orifice area (a), orifice to collimator distance (d), exposure time (t), average temperature (T), and the weight of target silver (CT/CS · Ws√110/107.88) have been previously described.
With the pressure at the melting point fixed, the best line for the solid phase was recalculated to give that shown in fig. 2. The applicable equation follows:
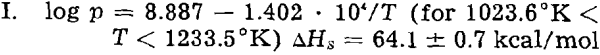
where ΔHs is the heat of sublimation.
Since the experimental data included in this paper cover only a relatively narrow portion of the liquid silver range, the curve for temperatures greater than 1233.5 °K has been recalculated to include the data of both von Wartenberg and Fischer for reasons to be discussed later.
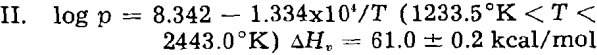
where ΔHv is the heat of vaporization. From this curve, the boiling point of silver is calculated to be 2443.0 °K.
Of the previous studies on the vapor pressure of silver, only one, that of Jones, Langmuir, and Mackay, covered the low-temperature range included in this work. Their results were obtained from free vaporization of silver from a heated filament, and it has been realized for some time that their values are much too low.

