This chart consists of triangles representing horizontal, vertical, and inclined distances. Any one unknown distance can be determined when the other two are known. For distances greater than the limits of the chart, divide the given dimensions by a figure to bring within the range of the chart. Multiply the result by the same figure to restore the proportions. Example: Conveyor 180 ft. horizontal distance, 48 ft. lift. Divide by 2, giving 90 ft. and 24 ft. The intersection of a vertical line from the*90 ft. HORIZONTAL DISTANCE with a horizontal line from the 24 ft. LIFT would occur at a point (on the 15° line) corresponding to a radius length of 93 ft. (approx.). Multiplying by 2, the actual incline length is 186 ft. The angle is 15° in both cases.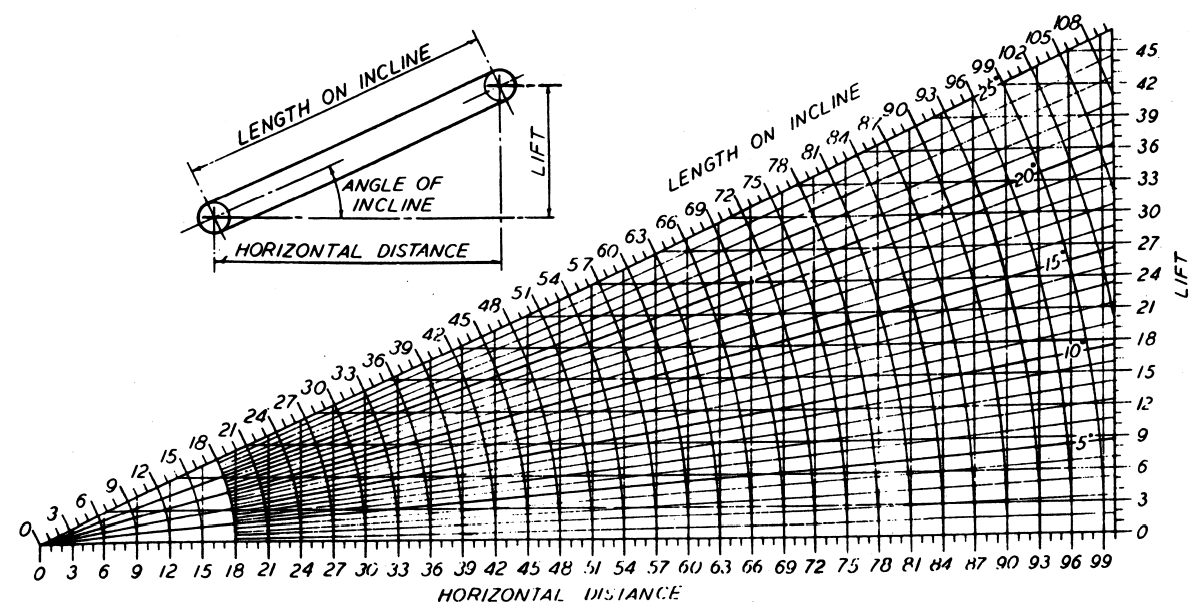
https://www.911metallurgist.com/estimating-conveyor-slope-angle

