In calculating the horse-power consumed by suction and by bucket dredges, figures have been taken from the various official reports on the mining industry in New Zealand, dates and pages in each instance being given. The calculations are made in theoretical horsepower, and for easy references are given in tabular form. The difference in the weight of the gravel lifted, while under the water level, has been disregarded; and, in estimating the steam power in compound engines, it is assumed that the low-pressure develops the same power as the high-pressure cylinder.
These results cannot be called conclusive, but they serve to show: (1.) That the frictional losses of power in gold-dredging are very great, probably 600 to 700 per cent, of the power theoretically sufficient to do the lifting work. (2.) That in bucket dredges, the actual engine power is roughly seven times that theoretically sufficient to do the work. (3.) That the suction dredge, working in exceptionally favourable circumstances—namely, where 95 per cent, of the material to be lifted was fine gravel—consumed 94.4 horsepower on the 47,745 foot-pounds of work required to raise 35 tons of solid material through 35 ft., together with the necessary water through 15 ft., while the Sew Hoy bucket dredge needed only 67.7 horsepower for the 54,130 foot-pounds of work necessary to raise 50 tons of solid material through 29 ft., and the necessary water through 15 ft., and the Kanieri dredge took only 107 horse-power to accomplish the 83,400 foot-pounds of work, representing the raising of 75 tons of solid material through 30 ft., and of the necessary water through 15 ft. It is, therefore, evident that, even in favourable circumstances, the suction dredge in gold dredging requires considerably more power than the bucket dredge, the excess being largely due to the large quantity of superfluous water lifted with the gravel. In proportion as the material becomes coarse, the consumption of power, of course, becomes greater. Mr. J. B. Jaquet, in his “Notes on Gold Dredging,” 1898, states: “As an instance of the costliness of the process (gold dredging by suction pumps), I may mention that a suction dredge, working upon the Waiparapa Beach, near the mouth of the Mataaura River, was found to require 60.7 h.-p. to lift on an average 15 tons of gravel per hour, whereas a bucket dredge of 30.7 h.-p. would lift many times this amount in the same time.”
The accuracy of the ratio established by the Table (see page 40) between the theoretical power required in the engine and the theoretical work to be done, expressed by the constant 7, may be tested by the coal consumption in the following cases.
Millar’s Creek dredge, with an output of 60 tons of solid material per hour, was fitted with an 18 h.-p. nominal engine for dredging, and a 10 h.-p. nominal engine for pumping—in all, 28 h.-p. nominal. The coal consumption was 326.6 lbs. per hour. Allowing 5 lbs. of coal per indicated horse-power, the total consumption represented about 65.3 indicated horse-power. Assuming the gravel, in this and the following cases, to have been lifted 30 ft., and the water to have been of normal quantity, and to have been raised 15 ft., the theoretical horse-power sufficient for the work would be about 9.3. The ratio between engine-power and work, therefore, in this instance, was very slightly over 7.
The Le Grand dredge, raising 50 tons of gravel and the normal quantity of water, consumed 280 lbs. of coal, representing 56 indicated horse-power, on a consumption of 5 lbs. per indicated horse-power per hour. Taking the height of lift as before, the horse-power theoretically sufficient for the work would be 8.5, giving a ratio of 6.6 between engine-power and work.
The Clyde dredge, raising 50 tons of gravel per hour, had the same coal consumption as the Le Grand, consequently the ratio was the same.
The Enterprise, lifting 75 tons of gravel per hour, was fitted with a compound 35 h.-p. nominal engine, burning 1/8 ton of coal per hour. In this case the coal consumption may have been somewhat less, say, 4 lbs. per indicated horse-power per hour. The total consumption, would, therefore, represent 70 indicated horse-power. The horse-power theoretically sufficient to raise the gravel and water was 11.6, which gives a ratio of rather over 6.
Messrs. Priestman state that in grab or clam-shell dredges lifting 50 tons per hour, the coal consumption is 2 lbs. per ton lifted per hour through, say, 30 ft. total lift. This does not include raising the necessary water for washing, and the output is calculated for favourable ground; the coal, too, is probably better than that in the foregoing estimates.
Steam-dipper dredges, including the driving of the pump for raising the water, probably require about twice the power per ton lifted as the bucket dredge. Hand-dipper dredges are operated by two or four hands at the winch.
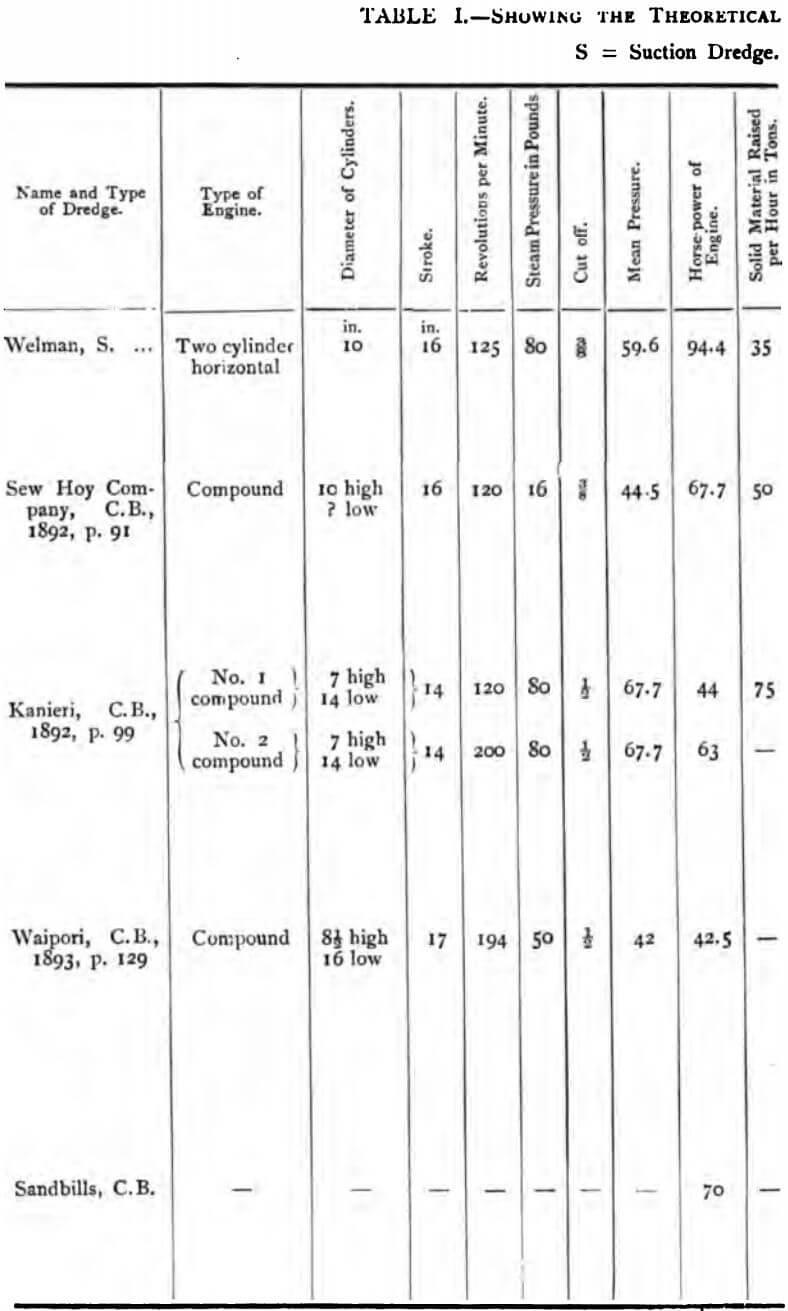
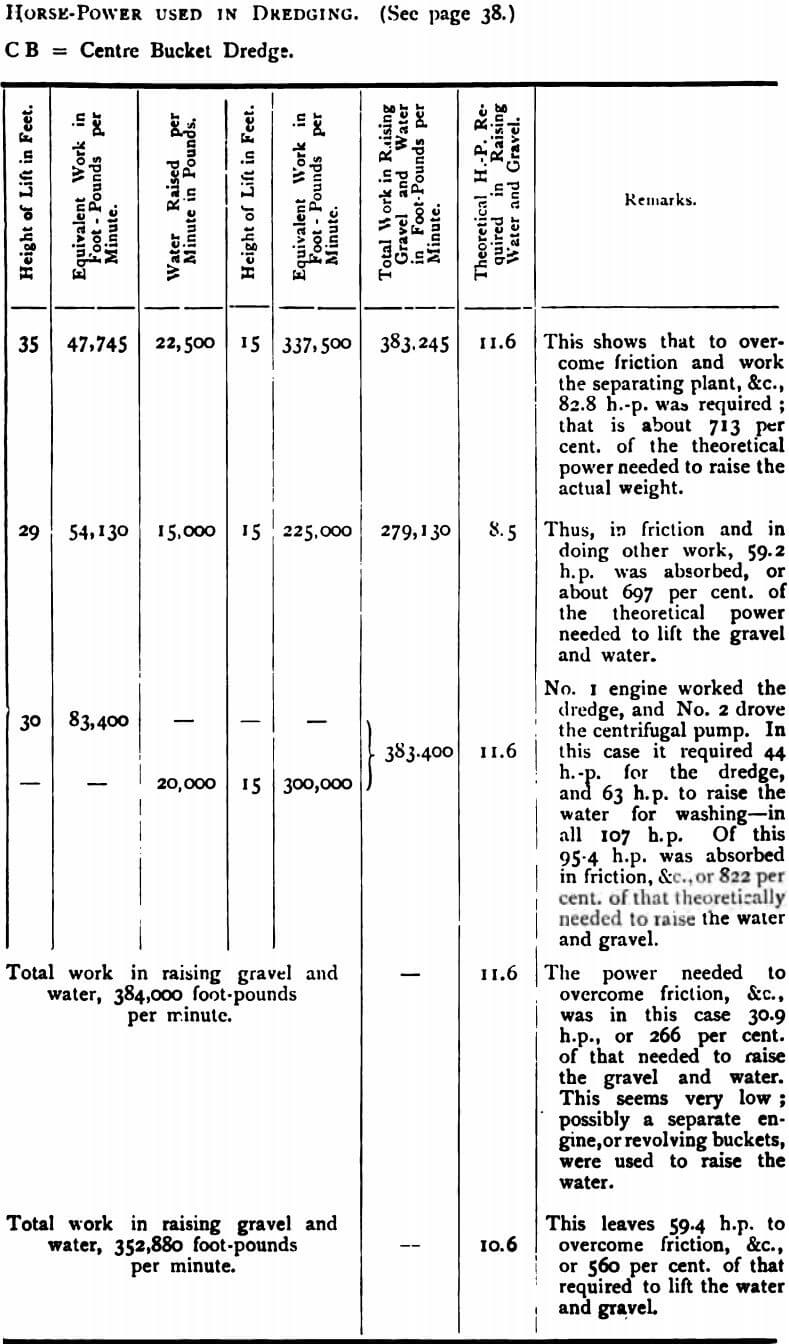
In the foregoing table, the ratio of the actual horse-power used to that theoretically needed for raising the gravel and washing water works out roughly at 7 to 1.
Both Messrs. Marshall, Sons, & Co., Limited, and Messrs. Lobnitz, Limited, consider that the working conditions are too variable to admit of any formula for the ready determination of the horse-power to be provided, and that each case must be dealt with on its requirements. Mr. P. R. Goedkoop, the London representative of Werf Conrad, Limited, of Haarlem, Holland, in reply to an inquiry from the author, wrote: —
“ A special formula does not exist, but generally the horse-power is calculated as follows: —
“ When you take the number of buckets and the capacity of each bucket, you get a theoretical figure for the production.
“ But the real production (the quantity of soil that passes through the screen) is only two-thirds of the theoretical production.
“ For all the machinery—that is, the dredging gear, screen, tailings elevator, and pump—the winches excluded, we take as rule 1½-h.-p. for each cubic metre of soil to be washed.
“For instance: A gold dredger has buckets of a capacity of 140 litres each, and the buckets run with a speed of 9 to 10 per minute; then the theoretical production is 80 cubic metres per hour.
“ But the real quantity to be washed is only two-thirds of 80 M³, or about 50 M³ per hour.
“ Therefore you want 50 x 1½= 75 i.-h.-p.
“ When the dredging gear, screen, elevator, and pump are all driven by the same engine, then 70 i.-h.-p. would be sufficient, as all these parts never use their maximum power at the same time.
“ But when you have a separate engine for the pump, then the total i.-h.-p. will be more than 75 i.-h.-p., because the pump takes 35 i.-h.-p. and the engine for dredging gear elevator and screen 45 i.-h.-p., together 80 i.-h.-p., or a little more than the 75 i.-h.-p. calculated before.
“ All those figures are calculated, taking that the pump has to produce a quantity of water ten times the quantity of the soil to be washed = 10 x 50 = 500 M³.
“ When you have very hard ground or clay you want more water, which increases at once the i.-h.-p.
“ Of course, there are always circumstances to be considered special with gold dredgers, when each dredger is designed to suit the ground to be worked, and that is the reason that there is not a more definitive formula as given above.”
